Codeforces Global Round 27

Codeforces Global Round 27 总结

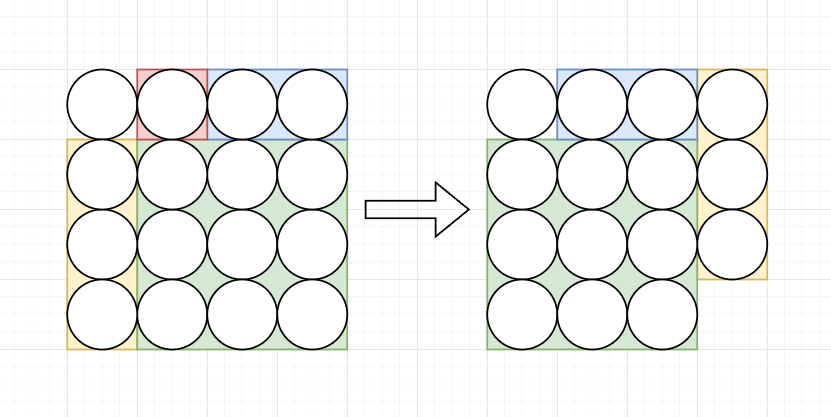
A

将红色的位置 \((r,c)\) 移走，分为三块来考虑，蓝色的块移动 \(m-c\)，黄色的块移动 \(m*(n-r)\)，绿色的块移动 \((m-1)*(n-r)\)。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>

using namespace std;
typedef long long ll;
const int N=1;
ll n,m,r,c;
void solve()
{
    cin>>n>>m>>r>>c;
    cout<<m-c+m*(n-r)+(m-1)*(n-r)<<'\n';
}
int main ()
{
    #ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
    #endif 
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int T;
    cin>>T;
    while(T--) solve();
    return 0;
}

B

首先 \(n\) 为 \(1\) 到 \(5\) 时，直接输出样例。到 \(n>5\) 的时候，\(n\) 为奇数就是 \(36366\) 每次在前面加上 \(33\)，否则就是 \(3366\) 每次在前面加上 \(33\)。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>

using namespace std;
typedef long long ll;
const int N=1;
int n;
void solve()
{
    cin>>n;
    if(n==1||n==3) cout<<-1<<'\n';
    else if(n==2) cout<<66<<'\n';
    else 
    {
        if(n&1)
        {
            for(int i=1;i<=n-5;i+=2) cout<<33;
            cout<<36366<<'\n';
        }
        else 
        {
            for(int i=1;i<=n-4;i+=2) cout<<33;
            cout<<3366<<'\n';
        }
    }
}
int main ()
{
    #ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
    #endif 
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int T;
    cin>>T;
    while(T--) solve();
    return 0;
}

C

构造题，观察到 \(5 \le n\)，不妨就考虑最后几位，因为可以保证最后几位受到的影响最小，思路是先考虑或出来最大，再考虑与上某个数不会影响或的数。

• \(n\) 为奇数，最后一次运算是按位与，所以 \(k \le n\)，且 \(n\) 必须在最后一位，前面按位或的结果要保留 \(n\) 有的所有位，不妨就只保证等于 \(n\)。将 \(n\) 拆开，用最后一位 \(1\)，也就是 \(lowbit(n)\) 和 \(n-lowbit(n)\) 相或得到 \(n\)，然后要保证 \(lowbit(n)\) 不被影响，可以与上 \(lowbit(n)\) 加上一位小的 \(1\)，这样的话可以确定最后四位：

\[lowbit(n),lowbit(n)+lowbit(n)==1 ? 2 : 1,n-lowbit(n),n \]

• \(n\) 为偶数，最后一次运算是按位或，所以可以填充所有位 \(k \le 2^t-1\)，\(t\) 表示 \(n\) 的二进制下的位数。
  • 考虑特殊情况 \(n=2^{t-1}\)，这样的话最高位就只能是 \(n\) 来给，所以不妨让最后一位为 \(n\)，然后前面的结果就是要为 \(n-1\)，但显然直接或上 \(n-1\) 的话不可能保住它，所以将 \(n-1\) 再拆开成 \(1\) 和 \(n-2\)，用 \(3\) 保住 \(1\)，用 \(n-1\) 保住 \(n-2\)，这样的话就能确定最后五位：
  \[1,3,n-2,n-1,n \]
  • 否则，用 \(n\) 的最高位 \(2^{t-1}\)，和 \(2^{t-1}-1\) 拼凑成 \(2^t-1\)。所以确定最后三位：
  \[2^{t-1},n,2^{t-1}-1 \]

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>

using namespace std;
typedef long long ll;
const int N=2e5+5;
int n;
int ans[N],v[N];
void solve()
{
    cin>>n;
    for(int i=1;i<=n;i++) ans[i]=0,v[i]=i;
    int a,b,c,d=0,e=0;
    
    if(n&1)
    {
        a=n&-n;
        cout<<n<<'\n';
        if(a==1) b=3;
        else b=a+1;
        c=n-a,d=n;
        ans[n]=d,ans[n-1]=c,ans[n-2]=b,ans[n-3]=a;
    }
    else 
    {
        int t=1;
        while(t<=n) t<<=1;
        cout<<t-1<<'\n';
        if(n!=t/2)
        {
            a=t/2,b=n,c=t/2-1;
            ans[n]=c,ans[n-1]=b,ans[n-2]=a;
        }
        else 
        {
            a=1,b=3,c=n-2,d=n-1,e=n;
            ans[n]=e,ans[n-1]=d,ans[n-2]=c,ans[n-3]=b,ans[n-4]=a;
        }
    }
    v[a]=v[b]=v[c]=v[d]=v[e]=0;
    int cnt=0;
    for(int i=1;i<=n;i++)
    {
        if(ans[i]) continue;
        while(!v[cnt]) cnt++;
        ans[i]=v[cnt++];
    }
    for(int i=1;i<=n;i++) cout<<ans[i]<<' ';
    cout<<'\n';
}
int main ()
{
    #ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
    #endif 
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int T;
    cin>>T;
    while(T--) solve();
    return 0;
}

D

结论比较好猜，就是尽可能将 \(2\) 都乘到最大的数上，但是有一个问题，前面的数不能乘后面的 \(2\)，就是说原本后面的数更小，但是可以乘上更多的 \(2\)。

因此将 \(a_i\) 的 \(2\) 拆出来统计个数，用一个单调栈维护，栈内单调递减，每次加入一个数，如果栈顶的元素小于这个数，就把栈顶的 \(2\) 全部给新加入的数。注意这里的新数大小是要目前有的 \(2\) 的。注意乘上以后会爆 long long。细节看代码吧。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>

using namespace std;
typedef long long ll;
const int N=2e5+5,mod=1e9+7;
int n;
ll a[N],v[N],b[N];
int st[N];
int qpow(int x,int y)
{
    int ret=1;
    while(y)
    {
        if(y&1) ret=1ll*ret*x%mod;
        x=1ll*x*x%mod;
        y>>=1;
    }
    return ret;
}
ll count(ll &x)
{
    if(!x) return 0;
    int ret=0;
    while(x%2==0) x/=2,ret++;
    return ret;
}
ll restore(ll x,ll y)
{
    while(y)
    {
        x<<=1;
        if(x>mod) return mod;
        y--;
    }
    return x;
}
void solve()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i],v[i]=count(a[i]);
    int tot=0;
    ll ans=0;
    for(int i=1;i<=n;i++)
    {
        ans=(ans+a[i]*qpow(2,v[i])%mod)%mod;
        while(tot&&a[b[tot]]<restore(a[i],v[i]))
        {
            ans=(ans-a[b[tot]]*qpow(2,v[b[tot]])%mod+mod)%mod;
            ans=(ans+a[b[tot]])%mod;
            ans=(ans-a[i]*qpow(2,v[i])%mod+a[i]*qpow(2,v[i]+v[b[tot]])%mod+mod)%mod;
            v[i]+=v[b[tot]];
            tot--;
        }
        b[++tot]=i;
        cout<<ans<<' ';
    }
    cout<<'\n';
}
int main ()
{
    #ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
    #endif 
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int T;
    cin>>T;
    while(T--) solve();
    return 0;
}