双向广搜
双向广搜(meet in the middle)
简介
双向广搜是搜索的一种进阶优化技巧，例如在已知终点和起点的情况下求是否能到达，需要走多远路。只从起点开始搜索可能会很费时间，那既然已知终点，为何不从终点同时开始进行搜索，看看是否能在中间相遇，也就是双向广搜(meet in the middle),也叫折半搜索。
如图：
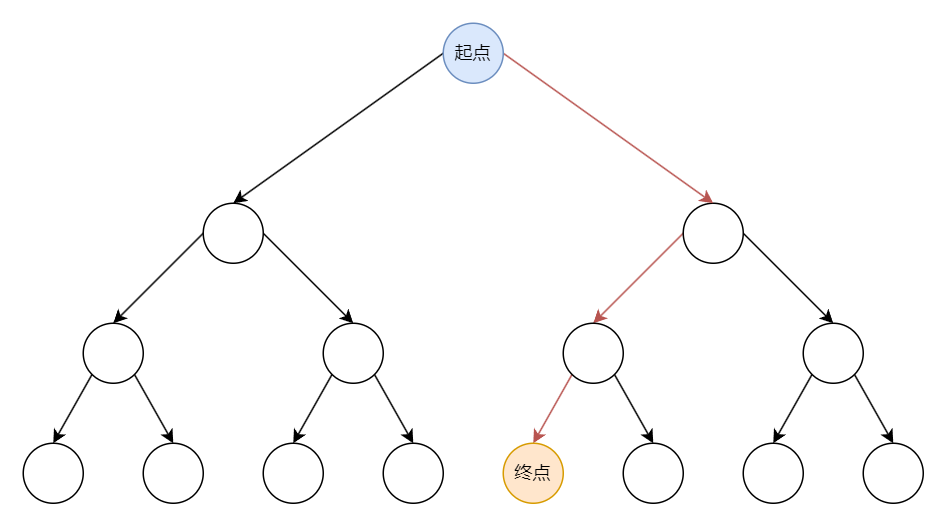
下面的图看起来都很舒心，而且，原先的解答树规模是 \(2^n\)，缩小到了 \(2 \times 2^{n/2}\)，小了不止半点，约为平方根级别，第张个图中和终点同层的点都不用去搜索，能省很大的时间空间，优化效果非常明显。
具体实现
双向广搜的一般实现方法有两种：
- 分成两个队列。正向 BFS 和逆向 BFS 的队列分开，适合正反2个BFS不平衡的情况。让子状态少的 BFS 先扩展下一层，另一个子状态多的 BFS 后扩展，任一队列的状态扩展完后就结束，可以减少搜索的总状态数，尽快相遇。例如：P1032 [NOIP2002 提高组] 字串变换。
- 合用一个队列。正向BFS和逆向 BFS 用同一个队列，适合正反2个 BFS 平衡的情况。正向搜索和逆向搜索交替进行，两个方向的搜索交替扩展子状态，先后入队。直到两个方向的搜索产生相同的子状态，即相遇了，结束。这种方法适合正反方向扩展的新结点数量差不多的情况。例如：P1379 八数码难题。
和普通 BFS 一样，双向广搜在扩展队列时也需要处理去重问题。把状态入队列的时候，先判断这个状态是否曾经入队，如果重复了，就丢弃。
P1032 [NOIP2002 提高组] 字串变换
分析
可以把每一次字符串变换的状态存入队列中，然后进行搜索。要由 \(A\) 变换到 \(B\)，也就是从 \(A\) 走到 \(B\)。已知终点和起点，统计最短的路程，可以使用双向广搜，使用 map 来记录每个状态到出发点的距离，进行扩展时记得交换变换规则。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=10;
int n=1;
string a[N],b[N];
string A,B;
int extend(queue<string>& q,map<string,int>&da,map<string,int> &db,string x[],string y[])
{
string t=q.front();
q.pop();
for(int i=0;i<t.size();i++)
for(int j=1;j<=n;j++)
if(t.substr(i,x[j].size())==x[j])
{
string s=t.substr(0,i)+y[j]+t.substr(i+x[j].size());
if(da.count(s)) continue;//原先出现过
if(db.count(s)) return da[t]+1+db[s];//相遇统计答案
da[s]=da[t]+1;
q.push(s);
}
return 11;
}
int bfs(string x,string y)
{
queue<string> qa,qb;//两个队列两个方向
map<string,int> da,db;//两个搜索到出发点的距离
qa.push(x),da[x]=0;
qb.push(y),db[y]=0;
//状态少的队列扩展完就结束
while(qa.size()&&qb.size())
{
int t;
//哪个少就扩展哪个
if(qa.size()<=qb.size()) t=extend(qa,da,db,a,b);
else t=extend(qb,db,da,b,a);
if(t<=10) return t;
}
return 11;
}
int main ()
{
cin>>A>>B;
while(cin>>a[n]>>b[n]) n++;
int ans=bfs(A,B);
if(ans>10) cout<<"NO ANSWER!"<<"\n";
else cout<<ans;
return 0;
}
另外说一下，s.substr(x,y) 表示复制字符串 \(s\) 的从下标 \(x\) 开始，长度为 \(y\) 的字符，s.substr(x) 表示复制字符串 \(s\) 的从下标 \(x\) 开始，一直到最后的字符。map 中的 count(s) 就是查找是否存在 \(s\) 的关键字。
P1379 八数码难题
分析
同样有起点和终点，不过初状态与末状态等价，两者相遇可用特殊的值来判断，比如初状态为 \(1\)，末状态为 \(2\)，那么判断相遇就是值为 \(3\) 的时候，细节见代码。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int ed=123804765,st,f[10][5]={{0,1},{1,0},{-1,0},{0,-1}},s[5][5];
map<int,int> vis,d;
int bfs(int a,int b)
{
queue<int> q;
vis[a]=1,d[a]=0;
vis[b]=2,d[b]=0;
q.push(a);q.push(b);
while(q.size())
{
int u=q.front();q.pop();
int v=u,x,y;
//将数放入网格
for(int i=3;i>=1;i--)
for(int j=3;j>=1;j--)
{
s[i][j]=v%10;
v/=10;
if(!s[i][j]) x=i,y=j;//找出0的位置
}
//将0进行移动
for(int i=0;i<4;i++)
{
int sx=x+f[i][0],sy=y+f[i][1];
if(sx<1||sx>3||sy<1||sy>3) continue;
swap(s[x][y],s[sx][sy]);
v=0;//还原成状态
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
v=v*10+s[i][j];
if(vis[v]==vis[u])
{
swap(s[x][y],s[sx][sy]);//还原后继续扩展
continue;
}
if(vis[v]+vis[u]==3) return d[u]+1+d[v];//起点为1，终点为2，相加为3
d[v]=d[u]+1;
vis[v]=vis[u];
q.push(v);
swap(s[x][y],s[sx][sy]);
}
}
return -1;
}
int main ()
{
cin>>st;
if(st==ed) cout<<0<<"\n";
else cout<<bfs(st,ed)<<"\n";
return 0;
}
[ABC336F] Rotation Puzzle
分析
翻转只有四种情况，最大操作次数为 \(20\)，直接搜索状态数可达 \(4^{20}=1099511627776\)，直接爆掉，但如果用双向搜索，每个方向最大深度为 \(10\)，这样状态数则为 \(2 \times 4^{10}=2097152\)，轻松通过。
和八数码一样，初末状态等价，可以只用一个队列，翻转操作需要略加思考，容易出错。可以用 string 和 map 实现 hash，将二维数组转化为字符串和字符串还原为数组与八数码相同。注意：原数组出现相同的数则一定无法实现，输出 -1，初末状态相同就不需要操作，输出 0。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=10;
int m,n,a[N][N],b[N][N],tong[N*N],f[5][3]={{1,1},{0,1},{1,0},{0,0}},c[N][N];
string st,ed;
map<string,int> vis,d,v;
string reverse(int x,int y)
{
string s;
for(int i=1;i<n;i++)
for(int j=1;j<m;j++)
c[i+x][j+y]=b[n-i+x][m-j+y];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
s+=c[i][j]+'0';
return s;
}
void restore(string s)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
c[i][j]=b[i][j]=s[(i-1)*m+j-1]-'0';
}
int bfs(string x,string y)
{
queue<string> q;
q.push(x);q.push(y);
vis[x]=1;d[x]=0;
vis[y]=2;d[y]=0;
while(q.size())
{
string t=q.front();q.pop();
for(int i=0;i<4;i++)
{
restore(t);
int l=f[i][0],r=f[i][1];
string s=reverse(l,r);
if(vis[s]==vis[t]) continue;
if(vis[s]+vis[t]==3) return d[s]+1+d[t];
d[s]=d[t]+1;
if(d[s]>10) return 21;
vis[s]=vis[t];
q.push(s);
}
}
return 21;
}
int main ()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
st+=a[i][j]+'0';
tong[a[i][j]]++;
}
for(int i=1;i<=n*m;i++)
{
if(tong[i]!=1)
{
cout<<-1<<"\n";
return 0;
}
ed+=i+'0';
}
if(ed==st)
{
cout<<0<<"\n";
return 0;
}
int ans=bfs(st,ed);
if(ans>20) cout<<-1<<"\n";
else cout<<ans<<"\n";
return 0;
}
