AtCoder Beginner Contest 338
ABC338 总结
A - Capitalized?
翻译
给你一个由大写和小写英文字母组成的非空字符串 \(S\)。请判断是否满足以下条件:
- \(S\) 的第一个字符是大写字母,其他所有字符都是小写字母。
如果满足,输出 Yes,否则输出 No。
分析
按题目说的判断即可。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n,m,t,a[N];
int main ()
{
string s;
cin>>s;
int st=1;
if(!(s[0]>='A'&&s[0]<='Z')) st=0;
for(int i=1;i<s.size();i++) if(!(s[i]>='a'&&s[i]<='z')) st=0;
if(st) cout<<"Yes";
else cout<<"No";
return 0;
}
B - Frequency
翻译
给你一个由小写英文字母组成的字符串 \(S\)。请找出在 \(S\) 中出现频率最高的字符。如果存在多个这样的字符,请输出按字母顺序排列最早的那个。
分析
用一个桶来计数,然后按字母顺序比较大小即可。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n,m,t,a[N];
int main ()
{
string s;
cin>>s;
for(int i=0;i<s.size();i++)
{
int id=s[i]-'a'+1;
a[id]++;
}
int maxx=0,ans;
for(int i=1;i<=26;i++)
{
if(a[i]>maxx)
{
maxx=a[i];
ans='a'+i-1;
}
}
cout<<(char)ans;
return 0;
}
C - Leftover Recipes
翻译
你的冰箱里有 \(N\) 种配料。我们称它们为配料 \(1\)、\(\dots\) 和配料 \(N\)。您有 \(Q_i\) 克配料 \(i\)。
您可以制作两种菜肴。制作一份 A 菜肴,需要 \(A_i\) 克配料 \(i\) \((1 \leq i \leq N)\)。制作一份 B 菜肴,需要 \(B_i\) 克配料 \(i\) \((1 \leq i \leq N)\)。每种菜肴只能做整数份。
输出最多总共可以制作多少份菜肴。
- \(1 \leq N \leq 10\)
- \(1 \leq Q_i \leq 10^6\)
- \(0 \leq A_i \leq 10^6\)
- There is an \(i\) such that \(A_i \geq 1\).
- \(0 \leq B_i \leq 10^6\)
- There is an \(i\) such that \(B_i \geq 1\).
- All input values are integers.
分析
设有做 \(x\) 份 A 菜和 \(y\) 份 B 菜,可知 \(x \times A_i+y \times B_i <=Q_i\) \((1 \leq i \leq N)\)。\(x\) 和 \(y\) 最大为 \(1e6\),同时枚举的话一定会超时。可以运用数学解二元方程的思想,先确定 \(x\),再考虑 \(y\)。
注意不要出现除以零的情况。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6;
ll n,m,t,q[20],a[20],b[20];
int main ()
{
cin>>n;
ll xm=0;
for(int i=1;i<=n;i++) cin>>q[i],xm=max(xm,q[i]);
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(a[i]) xm=min(xm,q[i]/a[i]);
}
for(int i=1;i<=n;i++) cin>>b[i];
ll ans=0;
for(int x=0;x<=xm;x++)
{
ll y=N;
for(int i=1;i<=n;i++)
{
if(q[i]<a[i]*x)
{
y=-N;
break;
}
else if(b[i]) y=min(y,(q[i]-a[i]*x)/b[i]);
}
ans=max(ans,x+y);
}
printf("%lld",ans);
return 0;
}
D - Island Tour
翻译
Atcoder 国里有 \(n\) 个小岛,第 \(i\) 个岛($1 \le i < n $)和第 \(i+1\) 个岛有一座桥连接,第 \(1\) 个岛和第 \(n\) 个岛有桥连接。
你想按照 \(s_1,s_2,s_3,\dots s_m\) 的顺序依次游览 \(m\) 座岛。只能通过桥从一个岛到另一个岛。
但现需要断开一座桥。问你任意选择一座桥断开的情况下,完成游览最少要通过多少次桥。
如果一座桥被多次计算,需要重复计算次数。
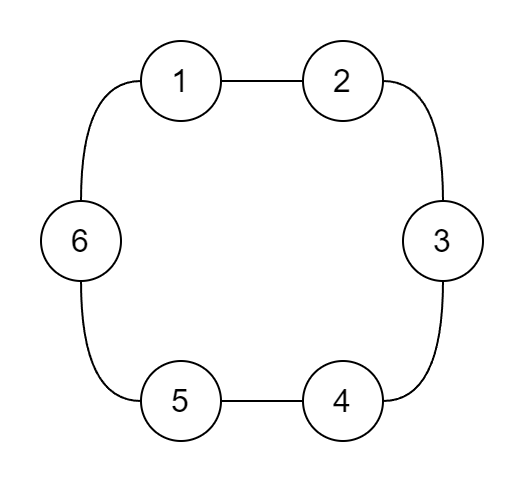
抽象化:有 \(n\) 个节点,第 \(i\) 号节点与第 \(i+1\) 号节点相连 \((1 \leq i < n)\),第 \(n\) 号节点与第 \(1\) 号节点相连组成一个环,边为双向边且长度为 \(1\)。下面给出一条路径,依次经过 \(s_1,s_2,s_3 \dots s_m\) 共 \(m\) 个点,求删去一条边后最短路径的长度为多少。
分析
可以分开考虑,只考虑从一点到另一点。由于是环,从一点到另一点只有两条路,要不顺时针,要不逆时针。
例如从 \(2\) 到 \(5\),写一个函数求 \(2\) 到 \(5\) 的顺时针的距离,那么反过来 \(5\) 到 \(2\) 的顺时针距离就是 \(2\) 到 \(5\) 的时针的距离。要注意从序号小的点到序号大的点和从序号大的点到序号小的点的区别。
接下来记录各边断开后走另一条路的长度,作为对答案的贡献。不过不能将环遍历一遍计算答案,复杂度就是 \(O(nm)\),直接爆炸。可以用差分的方式优化,是的,环上做差分。从序号小的点到序号大的点没有不同,但从序号大的点到序号小的点就有区别。
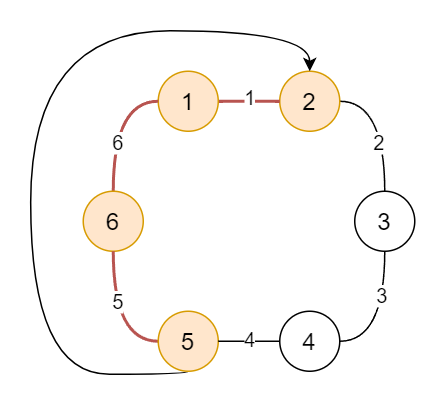
在数组上表现就是如此:
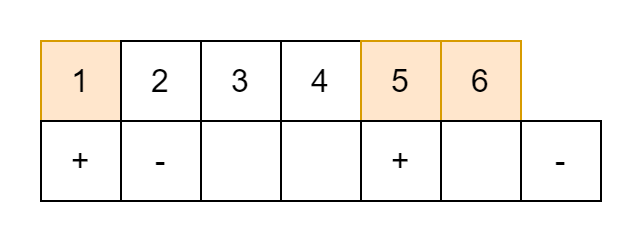
最后计算答案就好了。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
ll inf=LONG_LONG_MAX;
ll n,m,t,a[N],w[N];
ll dis(int x,int y)//x->y顺时针距离
{
return (x<=y) ? (y-x) :(y-x+n);
}
void count(int x,int y,ll v)//v表示如果断了走另一条的距离,x->y顺时针
{
if(x<=y)
{
w[x]+=v;
w[y]-=v;
}
else
{
w[x]+=v;
w[n+1]-=v;
w[0]+=v;
w[y]-=v;
}
}
int main ()
{
cin>>n>>m;
for(int i=1;i<=m;i++) cin>>a[i];
for(int i=1;i<m;i++)
{
count(a[i],a[i+1],dis(a[i+1],a[i]));
count(a[i+1],a[i],dis(a[i],a[i+1]));
}
ll ans=inf;
for(int i=1;i<=n;i++)
{
w[i]+=w[i-1];
ans=min(ans,w[i]);
}
printf("%lld\n",ans);
return 0;
}

