BST（二叉搜索树）
BST
基础芝士
给定一棵二叉树，每个节点有权值，定义“BST 性质”为：
对于树中的任意一个节点 \(x\) 都有：
- \(x\) 的权值大于 \(x\) 的左子树中任意节点的权值。
- \(x\) 的权值小于 \(x\) 的右子树中任意节点的权值。
即 \(左子树任意点的权值 < x < 右子树任意点的权值\)。
满足上述性质的二叉树即为“二叉搜索树”(BST)。可以发现，二叉搜索树的中序遍历的点权值单调递增。
一般情况下 BST 中无相同权值，当然有相同权值的也可以处理为无相同权值的。如图：
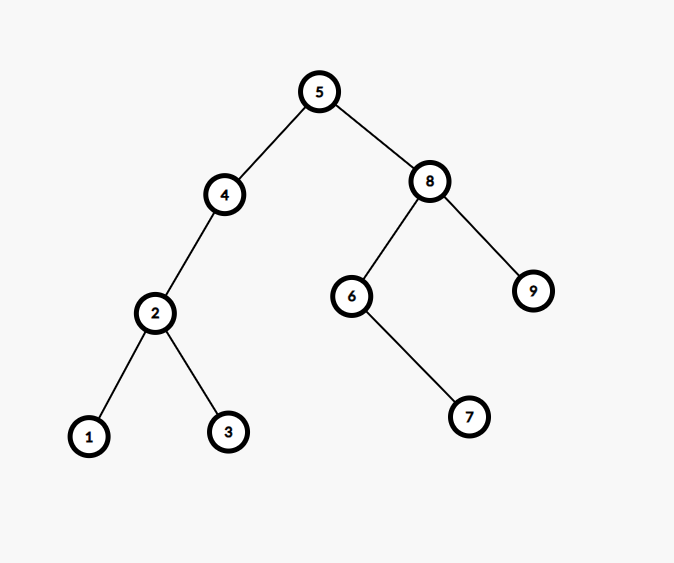
中序遍历结果为 \({1,2,3,4,5,6,7,8,9}\)。
维护操作
建立
为避免越界，一般在 BST 中插入正负无穷。仅由这两个节点构成的 BST 即为空 BST。如图：
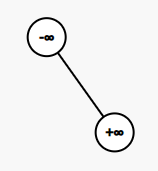
建立的操作即为建立一个空 BST：
const int inf=1<<30;
struct bst
{
int l,r,v;
}a[N];
int tot,root;
int New(int v)
{
a[++tot].v=v;
return tot;
}
void build()
{
New(-inf),New(inf);
root=1,a[1].r=2;
}
查找
查找 BST 中是否存在权值为 \(v\) 的节点。从根节点开始，利用“BST 性质”，一层层往下查找。
设当前所在节点为 \(x\)，权值为 \(y\)：
- \(y=v\)，则已找到。
- \(y>v\)，若 \(x\) 无左儿子，则说明不存在；若 \(x\) 有左儿子，进入左子树继续查找。
- \(y<v\)，若 \(x\) 无右儿子，则说明不存在；若 \(x\) 有右儿子，进入右子树继续查找。
用递归实现：
int find(int x,int v)
{
int y=a[x].v;
if(y==v) return x;
if(x==0) return 0; //若x不存在
return y>v ? find(a[x].l,v) : find(a[x].r,v);
}
用 while 实现：
int find(int v)
{
int x=root;
while(x)
{
int y=a[x].v;
if(y==v) break;
x= y>v ? a[x].l : a[x].r;
}
return x;
}
插入
在 BST 中插入一个权值为 \(v\) 的点（假设原来不存在）。
类似于查找操作：
设当前所在节点为 \(x\)，权值为 \(y\)：
- \(y>v\)，进入左子树继续查找。
- \(y<v\)，进入右子树继续查找。
- 若接下来进入的点为空，则直接建立。
用递归实现：
int insert(int &x,int v)//使用&，更新其父节点的信息
{
int y=a[x].v;
if(y==v) return ;
if(x==0)
{
x=New(v);
return ;
}
return y>v ? insert(a[x].l,v) : insert(a[x].r,v);
}
求最大/最小值
求以节点 \(x\) 为根节点的树的最大/最小值。在 BST 中，任一子树都是 BST，而 BST 的最小值一定在最左边的点上，最大值一定在最右边的点上（“BST 性质”）。如图：
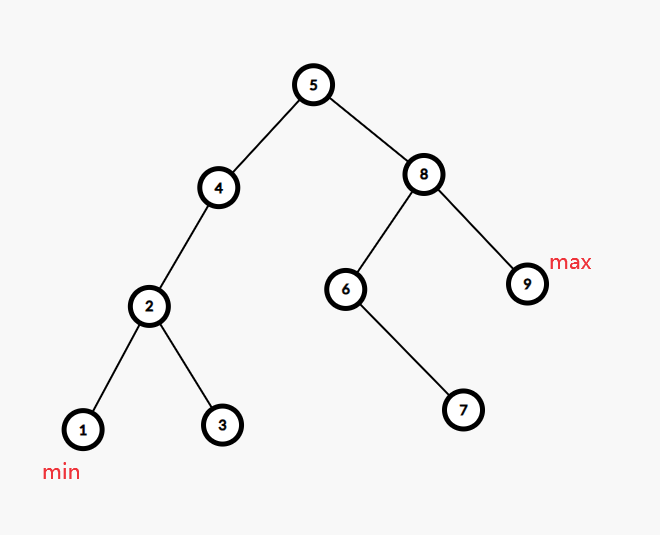
则求最大值就是从 \(x\) 开始一直向左子树走直到没有左子树，求最小值就是从 \(x\) 开始一直向右子树走直到没有右子树，当然要注意避开正负无穷。
int get_min(int x)
{
while(a[x].l) x=a[x].l;
return x;
}
int get_max(int x)
{
while(a[x].r) x=a[x].r;
return x;
}
求前驱/后继
设节点为 \(x\)，权值为 \(y\)。
- \(x\) 的前驱：指中序遍历 BST 后，位于 \(x\) 前的第一个点，即满足 \(v<y\) 的最大的 \(v\) 所对应的节点。
- \(x\) 的后继：指中序遍历 BST 后，位于 \(x\) 后的第一个点，即满足 \(v>y\) 的最小的 \(v\) 所对应的节点。
因此，求 \(x\) 的前驱即求 \(x\) 左子树中的最大值，求 \(x\) 的后继即求 \(x\) 右子树中的最小值。
int get_pre(int x)
{
return get_max(a[x].l);
}
int get_ne(int x)
{
return get_min(a[x].r);
}
若给出的是 \(y\)：
int get_pre(int u,int v)
{
if(u==0) return -inf;
if(a[u].v>=v) return get_pre(a[u].l,v);//先找到左子树
return max(a[u].v,get_pre(a[u].r,v));//再找到最大值
}
int get_ne(int u,int v)
{
if(u==0) return inf;
if(a[u].v<=v) return get_ne(a[u].r,v);//先找到右子树
return min(a[u].v,get_ne(a[u].l,v));//再找最小值
}
删除
从 BST 中删除权值为 \(v\) 的节点 \(x\)。
思考如何在删除 \(x\) 后能维护 BST。
- 若 \(x\) 的儿子个数小于2，则直接用 \(x\) 的儿子代替 \(x\) 的位置，与 \(x\) 的父节点相连。
- 若 \(x\) 的儿子个数等于2，考虑删除后，应该是 \(x\) 的后继 \(next\) 代替它的位置，也就是要先删除 \(next\)，再用 \(next\) 代替 \(x\)。而且 \(next\) 无左儿子，因为 \(next\) 是 \(x\) 右子树的最小值。所以，用 \(next\) 的右儿子代替 \(next\) 的位置，再用 \(next\) 代替 \(x\) 的位置。
void remove(int v)
{
int &x=root;//同时修改x父节点的信息
while(x)
{
int y=a[x].v;
if(y==v) break;
x= y>v ? a[x].l : a[x].r;
}
if(x==0) return;
if(a[x].l==0) x=a[x].r;
else if(a[x].r==0) x=a[x].l;
else
{
int next=get_ne(x);
remove(a[next].v);
a[next].l=a[x].l,a[next].r=a[x].r;
x=next;
}
}
结语
BST 中每一次操作的期望复杂度为 \(O(\log{n})\)，但 BST 容易退化。当 BST 为一条链时，复杂度为 \(O(n)\)。为了解决该问题，出现了各种平衡二叉树，请看：Treap。
tips
点权值中需满足“BST性质”的称为“关键码”，平衡二叉树中会区分开。
