P5663 加工零件 题解

P5663 加工零件 题解

原文链接：http://suo.im/5Xi8f9

确定做法

首先，看到这道题，我直接想到的是递归，于是复杂度就上天了，考虑最短路。

如何用最短路

首先，看一张图

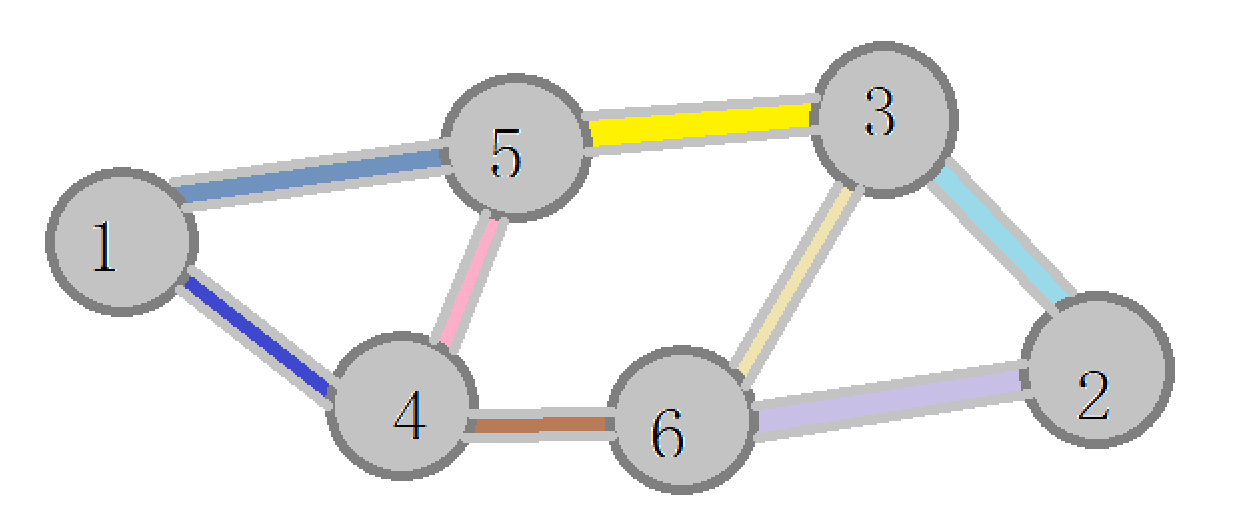
我们该如何解决问题？

问题: \(3\)做 \(5\)阶段的零件 \(1\)要不要做呢？

其实，实质就是看 \(3\)到 \(1\)有没有长度为 \(5\)的路径。

问题: \(3\)做 \(7\)阶段的零件 \(1\)要不要做呢？

其实，实质就是看 \(3\)到 \(1\)有没有长度为 \(7\)的路径。

问题: \(3\)做 \(6\)阶段的零件 \(1\)要不要做呢？

其实，实质就是看 \(3\)到 \(1\)有没有长度为 \(6\)的路径。

仔细思考这 \(3\)个问题，我们会发现，如果 \(3\)到 \(1\)有长度为 \(5\)的路径，那么 \(3\)到 \(1\)一定有长度为 \(7\)的路径，但并不一定有长度为 \(6\)的路径。

所以，我们要对每个点求一遍奇数路径，和偶数路径。

实现最短路

最短路的算法有很多，这道题最好用 \(dijkstra\)，或 \(bfs\)。

这道题的时限并不紧，并且 \(dijkstra\)细节太多，我就来演示 \(bfs\)实现的最短路

void bfw(){//我有一个好朋友叫bfw，所以我写bfs时，喜欢把函数名起为bfw
    memset(ji,0x3f,sizeof(ji));//奇数最短路径
    memset(ou,0x3f,sizeof(ou));//偶数最短路径
    queue<pair<int,int> >q;
    q.push(make_pair(1,0));
    ou[1]=0;
    while(q.size()){
        int x=q.front().first,y=q.front().second;
        for(int i=0;i<v[x].size();i++){
            if(y%2==1){//奇数+1=偶数
                if(y+1<ou[v[x][i]]){
                    ou[v[x][i]]=y+1;//更新答案
                    q.push(make_pair(v[x][i],y+1));
                }
            }else{//偶数+1=奇数
                if(y+1<ji[v[x][i]]){
                    ji[v[x][i]]=y+1;//更新答案
                    q.push(make_pair(v[x][i],y+1));
                }
            }
        }
        q.pop();
    }
}

\(v\)数组是一个动态数组，也就是 \(vector\)，曹老师教我们多用 \(STL\)写程序

如果你写这样的 \(bfs\)民间数据会 \(WA\) \(1\)个点 ，这个点是这样的

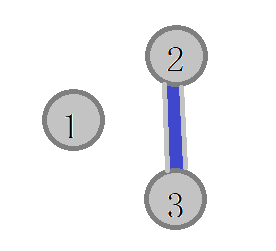
\(1\)号点是一个孤点，没有偶数路径，所以，我们的 \(bfs\)要这么写

void bfw(){//我有一个好朋友叫bfw，所以我写bfs时，喜欢把函数名起为bfw
    memset(ji,0x3f,sizeof(ji));//奇数最短路径
    memset(ou,0x3f,sizeof(ou));//偶数最短路径
    queue<pair<int,int> >q;
    for(int i=0;i<v[1].size();i++){
        ji[v[1][i]]=1;
        q.push(make_pair(v[1][i],1));
    }
    while(q.size()){
        int x=q.front().first,y=q.front().second;
        for(int i=0;i<v[x].size();i++){
            if(y%2==1){//奇数+1=偶数
                if(y+1<ou[v[x][i]]){
                    ou[v[x][i]]=y+1;//更新答案
                    q.push(make_pair(v[x][i],y+1));
                }
            }else{//偶数+1=奇数
                if(y+1<ji[v[x][i]]){
                    ji[v[x][i]]=y+1;//更新答案
                    q.push(make_pair(v[x][i],y+1));
                }
            }
        }
        q.pop();
    }
}

简要讲解主程序

有了这些主程序应该是很简单的了

int main(){
    int n,m,q;
    read(n);read(m);read(q);
    for(int i=1;i<=m;i++){
        int x,y;
        read(x);read(y);//无向边
        v[x].push_back(y);//连边
        v[y].push_back(x);//连边
    }
    bfw();//跑最短路
    while(q--){
        int x,y;
        read(x);read(y);
        if(y%2==0){
            if(ou[x]>y)puts("No");//如果大于就不可能了
            else puts("Yes");
        }else{
            if(ji[x]>y)puts("No");//如果大于就不可能了
            else puts("Yes");
        }
    }
    return 0;
}

总结

先来看一看这题完整的代码了

#include <bits/stdc++.h>
using namespace std;
template<typename T>inline void read(T &FF){
    T RR=1;FF=0;char CH=getchar();
    for(;!isdigit(CH);CH=getchar())if(CH=='-')RR=-1;
    for(;isdigit(CH);CH=getchar())FF=(FF<<1)+(FF<<3)+(CH^48);
    FF*=RR;
}
template<typename T>void write(T x){
    if(x<0)putchar('-'),x*=-1;
    if(x>9)write(x/10);
    putchar(x%10+48);
}
vector<int>v[100010];
int ji[100010],ou[100010];
void bfw(){//我有一个好朋友叫bfw，所以我写bfs时，喜欢把函数名起为bfw
    memset(ji,0x3f,sizeof(ji));//奇数最短路径
    memset(ou,0x3f,sizeof(ou));//偶数最短路径
    queue<pair<int,int> >q;
    for(int i=0;i<v[1].size();i++){
        ji[v[1][i]]=1;
        q.push(make_pair(v[1][i],1));
    }
    while(q.size()){
        int x=q.front().first,y=q.front().second;
        for(int i=0;i<v[x].size();i++){
            if(y%2==1){//奇数+1=偶数
                if(y+1<ou[v[x][i]]){
                    ou[v[x][i]]=y+1;//更新答案
                    q.push(make_pair(v[x][i],y+1));
                }
            }else{//偶数+1=奇数
                if(y+1<ji[v[x][i]]){
                    ji[v[x][i]]=y+1;//更新答案
                    q.push(make_pair(v[x][i],y+1));
                }
            }
        }
        q.pop();
    }
}
int main(){
    int n,m,q;
    read(n);read(m);read(q);
    for(int i=1;i<=m;i++){
        int x,y;
        read(x);read(y);//无向边
        v[x].push_back(y);//连边
        v[y].push_back(x);//连边
    }
    bfw();//跑最短路
    while(q--){
        int x,y;
        read(x);read(y);
        if(y%2==0){
            if(ou[x]>y)puts("No");//如果大于就不可能了
            else puts("Yes");
        }else{
            if(ji[x]>y)puts("No");//如果大于就不可能了
            else puts("Yes");
        }
    }
    return 0;
}

这道题还是比较有思维含量的，民间数据也出的很好，让我们思考全面。

---

分享一下我的dijkstra做法

原文链接：http://suo.im/6jM79g

这题是CSPJ2019的第四题。

很遗憾，我考试时还没有学过图论，所以不会做。

但是考场上想到了奇偶性，可因为稍微复杂，为了拿分还是打了暴力。

考场上的分绝对不能轻易放弃！怀着侥幸心理，我在考场上写下了这段代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,q;
int u,v;
int aa,ll;
bool flag;
int a[10005][10005],num[10005];//由于当时不会存图，于是用了一种类似于邻接矩阵的东西来存
/为了防止MLE故意开小
void dfs(int t,int l){//其实不算dfs...只是单纯的扩展。
    //l表示当前生产
    //t代表编号
    if(l==-1)return;//边界条件
    if(flag)return;//flag表示1号点是否提供原材料，算是剪枝吧
    if(t==1&&l==0){//如果1号点提供
        flag=true;//此时有解
        return;
    }
    for(int i=1;i<=num[t];++i){//num代表此点有多少传送带连接
        dfs(a[t][i],l-1);
        //向周围其它的点扩展，索求上一阶段材料
    }
}           
int main(){

    cin>>n>>m>>q;
    for(int i=1;i<=m;++i){
        cin>>u>>v;
        ++num[u];++num[v];
        a[u][num[u]]=v;
        a[v][num[v]]=u;
        //无向图，都存
    }
    for(int i=1;i<=q;++i){
        cin>>aa>>ll;
        flag=false;/初始化（当时因为这个调半天）
        dfs(aa,ll);//爆搜去！
        if(flag)cout<<"Yes"<<endl;//有解
        else cout<<"No"<<endl;//无解
    }
    fclose(stdin);fclose(stdout);//忘了删了=w=
    return 0;
}

然而这个代码肯定会T的，因为写的时候就是为了拿暴力分

爆搜不T数据垃圾

期望得分：40分

luogu数据得分：50分

官方数据得分：40分

在此为机房大佬 @蒻蒻蒻蒻蒻 没删调试白给100分默哀

很遗憾，考后第一次上课就讲起了图论...

于是我左看右看上看下看，

终于理解了链式前向星

学会了单源最短路径

经过大佬们的启发后

发现这题的确和奇偶性有关

算法标签：奇偶性，最短路

分析一下，

本题的实质是：从a到1好点有没有长度为L+1的路径

其实路径不一定要长度为L+1。

因为本题有个神操作就是：我让你提供给我材料你却还来找我要。 好好体会这句话

于是我们的材料就可以在这两点间反复横跳，直到为0。

为什么这么说大家可以参考别的题解或者自己画个图。。。

那么对于此题，我用的是dijkstra（因为只会这个）

其实宽搜和SPFA就可以A掉，只不过我想把dij练得熟练一点。

我们开两个二维数组： \(dis[N][2] \ \And\ vis[N][2]\);

其实和dij模板没什么区别。

开二维就是为了存储1到a号点的奇数路径长度和偶数路径长度

前提是还得小于L，否则够不到

如果该店没有奇数或偶数长度的路径，由于dis数组初值为INF,一定大于L所以不用管

唯一一个毒瘤点需要特判：1号点没有任何传送带时肯定不行啊

CODE：

#include<bits/stdc++.h>
#define ll long long
#define reg register
#define N 1000005

//个人习惯
using namespace std;
int n,m,c,head[N],cnt,dis[N][2];
bool vis[N][2];
struct node{
    int data,dis;//data序号，dis已知最短距离
    bool operator < (const node &a)const{
        return a.dis < dis;//使小根堆顶为目前已知最近的点
    }
};
//重置运算符来给小根堆用

priority_queue<node>q;
//小根堆
struct Edge{
    int to,next;
}e[N];

void add(int u,int v){
    //无权图长度默认为1
    e[++cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt; 
}

//链式前向星存图

void Initialization(){
    memset(dis,0x3f,sizeof(dis));
    q.push((node){1,0});
    dis[1][0] = 0;
}

//初始化，先将1点入堆，且dis赋值为INF,而1号点为0。

void dijkstra(){//dijkstra算法
    while(!q.empty()){//只要队列不空
        node tmp = q.top();
        q.pop();//出栈，旧的不去新的不来
        int now = tmp.data;//当前以那个点向周围扩展
        for(int i = head[now]; i ;i = e[i].next){//链式前向星遍历
            int y = e[i].to;
            if(dis[y][0] > dis[now][1] + 1){//奇数走一步为偶数
                dis[y][0] = dis[now][1] + 1;
                if(!vis[y][0]){
                    vis[y][0] = 1;
                    q.push((node){y,dis[y][0]});//入队列
                }
            }
            if(dis[y][1] > dis[now][0] + 1){//偶数走一步为奇数
                dis[y][1] = dis[now][0] + 1;
                if(!vis[y][1]){
                    vis[y][1] = 1;
                    q.push((node){y,dis[y][1]});//入队列
                }
            }
        }
    }
}

int main(){
    cin>>n>>m>>c;
    for(int i = 1 ; i <= m ; ++i ){
        int u,v;
        cin>>u>>v;
        add(u,v);
        add(v,u);//无向图注意存两次
    }
    //无聊的输入
    Initialization();
    dijkstra();
    //这样写清楚一点

    while(c--){
        int a,l;
        cin>>a>>l;
        if(!head[1]){
            puts("No");//如果1号点没有传送带连接
        }
        else if(dis[a][l%2]<=l)puts("Yes");//只要l%2路径<L
        else puts("No");//否则
        //puts自动换行。。。懒得打了
    }
    //return 233;（雾）
}

然后就愉快地AC啦！