图

概要

笔试中经常出现关于图的考题，有必要熟悉下。本篇参考《大话数据结构》，简单介绍一下图，不作深入探究。

 

---

定义

图的简单定义

 
图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：\(G(V,E)\)，其中 \(G\) 表示一个图，\(V\) 是图 \(G\) 中点的集合，\(E\) 是图 \(G\) 中边的集合。

对于图的定义，我们需要几个注意的地方。

• 线性表中我们把数据元素叫元素，树中将数据元素叫结点，在图中数据元素称为顶点。
• 线性表中可以没有数据元素，称为空表。树中可以没有结点，叫做空树。但是在图结构中，不允许没有顶点。在定义中强调了点的集合 \(V\) 有穷非空。
• 线性表中，相邻的数据元素之间具有线性关系，在树结构中，相邻两层的结点具有层次关系，而图中，任意两个顶点之间都有可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的

无向边：若顶点 \(v_i\) 到 \(v_j\) 之间的边没有方向，则称这条边为无向边，用无序偶对 \((v_i, v_j)\) 来表示。

无向图：如果图中任意两个顶点之间的边都是无向边，则称该图为无向图。下图左就是无向图，由于是无方向的，连接顶点 \(A\) 与 \(D\) 的边，可表示成无序对 \((A,D)\)，也可以写成 \((D,A)\).

上图左的无向图 \(G_1\) 可表示成 \(G_1=(V_1, \{E_1\})\)，其中顶点集合 \(V_1=\{A,B,C,D\}\)，边集合 \(E_1=\{ (A,B),(B,C), (C,D),(D,A),(A,C) \}\).

有向边：若顶点 \(v_i\) 到 \(v_j\) 之间的边有方向，则称这条边为有向边，也称为弧。用有序偶对 \(\langle v_i,v_j \rangle\) 来表示。\(v_i\) 称为弧尾，\(v_j\) 称为弧头。

有向图：如果图中任意两个顶点之间的边都是有向边，则称该图为有向图。上图右就是有向图，连接顶点 \(A\) 与 \(D\) 的有向边就是弧，\(A\) 是弧尾，\(D\) 是弧头，\(\langle A,D \rangle\) 表示弧，注意不能写成 \(\langle D,A \rangle\).

上图右的有向图 \(G_2\) 可表示成 \(G_2=(V_2, \{E_2\})\)，其中顶点集合 \(V_2=\{A,B,C,D\}\)，弧集合 \(E_2=\{ \langle A,D \rangle, \langle B,A \rangle, \langle C,A \rangle,\langle B,C \rangle \}\).注意无向边用圆括号 “\(()\)” 表示，而有向边则是用尖括号“\(\langle \rangle\)” 表示。

在图中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。如下边两个图都不是简单图。

在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。含有 \(n\) 个顶点的无向完全图有 \(\dfrac{n(n-1)}{2}\) 条边。

在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图，含有 \(n\) 个顶点的有向完全图有 \(n(n-1)\) 条边。

有很少条边或弧的图称为稀疏图，反之称为稠密图。

有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网。如下图就是一张带有权的图，即标识中国四大城市的直线距离的网，此图中的权就是两地的距离。

假设有两个图 \(G=(V,\{E\})\) 和 \(G‘=(V’,\{E‘\})\)，如果 \(V' \subseteq V\) 且 \(E' \subseteq E\)，则称 \(G'\) 为 \(G\) 的子图。

 

图的顶点与边间关系

 
对于无向图 \(G=(V,\{E\})\)，如果边 \((v,v') \in E\)，则称顶点 \(v\) 和 \(v'\) 互为邻接点，即 \(v\) 和 \(v'\) 相邻接，边 \((v,v')\) 依附于顶点 \(v\) 和 \(v'\)，或者说 \((v,v')\) 与顶点 \(v\) 和 \(v'\) 相关联。顶点 \(v\) 的度是和 \(v\) 相关联的边的数目，记为 \(TD(v)\).

对于有向图 \(G=(V,\{E\})\)，如果弧 \(\langle v,v'\rangle \in E\)，则称顶点 \(v\) 邻接到顶点 \(v'\)，顶点 \(v’\) 邻接自 \(v\)，弧 \(\langle v,v'\rangle\) 和顶点 \(v\) 和 \(v'\) 相关联。以顶点 \(v\) 为头的弧的数目称为 \(v\) 的入度，记为 \(ID(v)\)；以 \(v\) 为尾的弧的数目称为 \(v\) 的出度，记为 \(OD(v)\)；顶点 \(v\) 的度为 \(TD(v)=ID(v)+OD(v)\).

无向图 \(G=(V,\{E\})\) 中从顶点 \(v\) 到顶点 \(v'\) 的路径是一个顶点序列 \((v=v_{i,0}, v_{i,1}, \cdots, v_{i,m}=v')\)，其中 \((v_{i,j-1}, v_{i,j}) \in E,1 \leqslant j \leqslant m\). 如果 \(G\) 是有向图，则路径也是有向的，顶点序列应满足 \(\langle v_{i,j-1}, v_{i,j} \rangle \in E, 1\leqslant j \leqslant m\).

路径的长度是路径上的边或弧的数目。

第一个顶点到最后一个顶点相同的路径称为回路或环。序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。

 

连通图相关术语

 
在无向图 \(G\) 中，如果从顶点 \(v\) 到顶点 \(v'\) 有路径，则称 \(v\) 和 \(v'\) 是连通的。如果对于图中任意两个顶点 \(v_i,v_j \in E\)，\(v_i\) 和 \(v_j\) 都是连通的，则称 \(G\) 是连通图。

无向图中的极大连通子图称为连通分量。注意连通分量的概念，它强调

• 要是子图
• 子图要是连通的
• 连通子图含有极大顶点数
• 具有极大顶点数的连通子图包含依附于这些顶点的所有边

在有向图 \(G\) 中，如果对于每一对 \(v_i,v_j \in V\)，\(v_i \neq v_j\)，从 \(v_i\) 到 \(v_j\) 和从 \(v_j\) 到 \(v_i\) 都存在路径，则称 \(G\) 是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。

无向图中连通且 \(n\) 个顶点 \(n-1\) 条边叫生成树。有向图中一顶点入度为 \(0\) 其余顶点入度为 \(1\) 的叫有向树。一个有向图由若干棵有向树构成生成森林。

 

---

图的遍历

图的遍历是和树和遍历类似，我们希望从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历。
 

深度优先遍历

 
深度优先遍历（Depth_First_Search），也有称为深度优先搜索，简称为 DFS。

比如下图左：

首先我们从顶点 \(A\) 开始，做上走过的记号后，面前有两条路，通向 \(B\) 和 \(F\)，我们给自己定一个原则，在没有碰到重复顶点的情况下，始终是向右手边走，于是走到了 \(B\) 顶点。整个行路过程，可参看上图的右图。如果此时的顶点的相邻顶点都做了记号表示走过，那就向后退回再做判断，直到遍历所有点。

深度优先遍历其实就是一个递归的过程。它从图中某个顶点 \(v\) 出发，访问此顶点，然后从 \(v\) 的未被访问的邻接点出发深度优先遍历图，直至图中所有和 \(v\) 有路径相通的顶点都被访问到。
 

广度优先遍历

 
广度优先遍历（Breadth_First_Search）又称为广度优先搜索，简称 BFS。

如果说图的深度优先遍历类似树的前序遍历，那么图的广度优先遍历就类似于树的层序遍历了。如下图

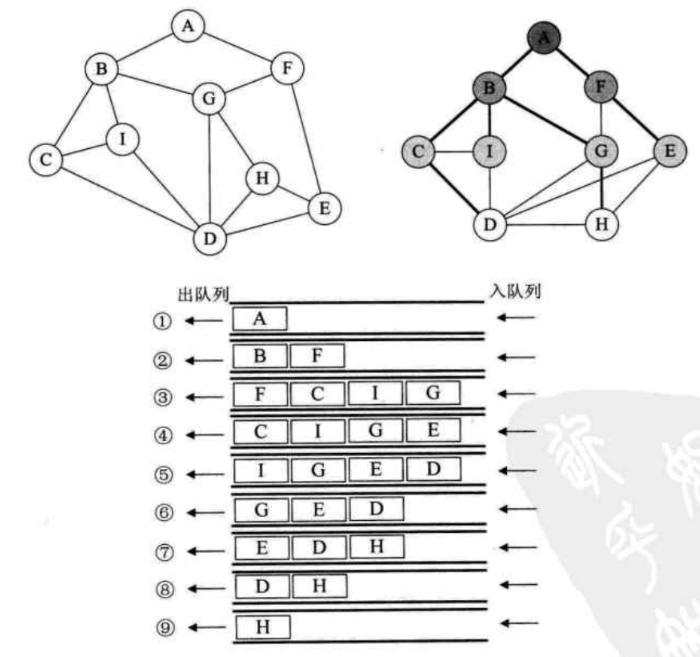
我们将上图左稍微变形，变形原则是顶点 \(A\) 放置在最上第一层，让与它有边的顶点 \(B,F\) 这第二层，再让与 \(B\) 和 \(F\) 有边的顶点 \(C,I,G,H\) 为第三层，再将这四个顶点有边的 \(D,H\) 放在第四层，如上图右所示。此时视觉上感觉图的形状发生了变化，其实顶点和边的关系还是完全相同的。

对比图的深度优先遍历与广度优先遍历，它们在时间复杂度上是一样的，不同之处仅仅在于对顶点访问的顺序不同。
 

---

最小生成树

一个连通图的生成树是一个极小的连通子图，它含有图中全部的顶点，但只有足以构成一棵树的 \(n-1\) 条边。我们把构造连通网（当然带权值）的最小代价生成树称为最小生成树。找连通网的最小生成树，经典的有两种算法，普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。
 

Prim 算法

 
为了能讲明白这个算法，我们先构造图的邻接矩阵，如下图：

现在我们有了一个存储结构为 MGraph 的 \(G\). \(G\) 有 \(9\) 个顶点，它的 arc 二维数组如上图右。

假设 \(N=(P,\{TE\})\) 是连通网，\(TE\) 是 \(N\) 上最小生成树中边的集合。算法从 \(U=\{u_0\}\)（\(u_0 \in V\)），\(TE= \{\}\) 开始。重复执行下述操作：在所有 \(u \in U, v \in V-U\) 的边 \((u,v) \in E\) 中找一条代价最小的边 \((u_0,v_0)\) 并入集合 \(TE\)，同时 \(v_0\) 并入 \(U\)，直到 \(U=V\) 为止。此时 \(TE\) 中必有 \(n-1\) 条边，则 \(T=(V,\{TE\})\) 为 \(N\) 的最小生成树。 其算法时间复杂度为 \(O(n^2)\).

 

Kruskal 算法

 
Prim 算法经某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树的，而 Kruskal 算法把焦点转身图的边，直接找最小权值的边来构建生成树，只不过构建时要考虑是否会形成环路而已。

假设 \(N=(P,\{E\})\) 是连通网，则令最小生成树的初始状态为只有 \(n\) 个顶点而无边的非连通图 \(T=(V,\{\})\)，图中每个顶点自成一个连通分量。然后在 \(E\) 中选择代价最小的边，若该边依附的顶点落在 \(T\) 中不同的连通分量上（防止形成环），则将此边加入到 \(T\) 中，否则舍去此边而选择下一条代价最小的边。依此类推，直至 \(T\) 中所有顶点都在同一连通分量上为止。此算法的时间复杂度和边数 \(e\) 有关，算法时间复杂度为 \(O(e\log e)\).
 

Prim 算法和 Kruskal 算法对比

 
KrusKal 算法主要是针对边来展开，边数少时效率会非常高，所以对于稀疏图有很大的优势。而 Prim 算法对于稠密图，即边数非常多的情况会更好一些。
 

---

最短路径

网图的最短路径是指两顶点之间经过的边上权值之和最小的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点。

常见的有两种算法：迪杰斯特拉（Dijkstra）算法和弗洛伊德（Floyd）算法。
 

Dijkstra 算法

 

这是一个按路径长度递增的次序产生最短路径的算法。它的思路大体是这样的：

比如说要找下图中顶点 \(v_0\) 到点 \(v_1\) 的最短距离，显然就是 \(1\)，路径就是直接 \(v_0\) 到 \(v_1\).

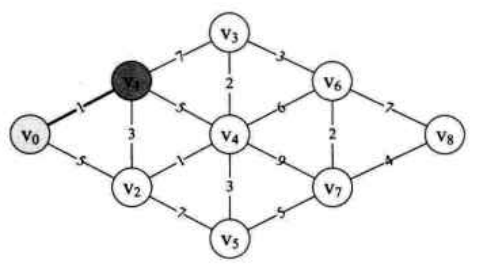
由于顶点 \(v_1\) 还与 \(v_2,v_3,v_4\) 连线，所以此时我们同时求得了 \(v_0 \rightarrow v_1 \rightarrow v_2=1+3=4\)，\(v_0 \rightarrow v_1 \rightarrow v_3=1+7=8\)，\(v_0 \rightarrow v_1 \rightarrow v_4=1+5=6\).

现在求 \(v_0\) 到 \(v_2\) 的最短距离，因为 \(v_0 \rightarrow v_1 \rightarrow v_2=4\) 小于 \(v_0 \rightarrow v_3=5\)，所以 \(v_0\) 到 \(v_2\) 的最短距离为 \(4\). 由于顶点 \(v_2\) 还与 \(v_4,v_5\) 连线，所以此时我们同时求得了 \(v_0 \rightarrow v_2 \rightarrow v_4 = 4+1=5\)， \(v_0 \rightarrow v_2 \rightarrow v_5=4+7=11\). 此时可以判断，由于 \(v_0 \rightarrow v_1 \rightarrow v_2 \rightarrow v_4=5\) 要比 \(v_0 \rightarrow v_1 \rightarrow v_4\) 还要小。所以 \(v_0\) 到 \(v_4\) 目前的最小距离是 \(5\).

过程中基于已经求出的最短路径的基础上，继续向前一步步推，就可以求出 \(v_0\) 到 \(v_8\) 的最短路径了。其时间复杂度为 \(O(n^2)\).

 

Floyd 算法

 
为了能讲明白 Floyd 算法的精妙所在，我们先看一个例子。如下图所示。

我们先定义两个二维数组 \(D[9,9]\) 和 \(P[9,9]\)，\(D\) 代表顶点到顶点的最短路径权值的矩阵。\(P\) 代表对应顶点的最小路径的前驱矩阵。在未分析任何顶点之前，我们将 \(D\) 命名为 \(D^{-1}\)，其实它就是初始的图的邻接矩阵。将 \(P\) 命名为 \(P^{-1}\)，初始化为图中所示的矩阵。

首先我们来分析，所有的顶点经过 \(v_0\) 后到达另一顶点的最短路径，显然 \(v_0\) 到其它点的路径是不会有变化的，和初始化一样。接下来求经过 \(v_1\) 时，原本 \(D[0][2]=5\)，现在由于 \(D[0][1]+D[1][2]=4\). 取较小值，所以 \(D[0][2]=4\)，同理可得 \(D[0][3]=8\)，\(D[0][4]=6\)，然后再依次分析经过顶点 \(v_2, v_3, \cdots\) 等。由于这些最小权值的修正，所以在路径矩阵 \(P\) 上，也要做处理，将它们改为当前的 \(P[v][k]\) 值。最终结果如下：

得到上述矩阵后，求最短路径也很容易。比如求 \(v_0\) 到 \(v_8\) 的最短路径，由于 \(P[0][8]=1\)，得到要经过顶点 \(v_1\)，然后将 \(1\) 取代 \(0\) 得到 \(P[1][8]=2\)，说明要经过 \(v_2\)，又 \(P[2][8]=4\)，说明要经过 \(v_4\)，然后 \(P[4][8]=3\)，说明要经过 \(v_3\) \(\cdots\)， 这样就得到了最短路径值为 \(v_0\rightarrow v_1 \rightarrow v_2 \rightarrow v_4 \rightarrow v_3 \rightarrow v_6 \rightarrow v_7 \rightarrow v_8\).

该算法的时间复杂度为 \(O(n^3)\). 如果需要求所有顶点至所有顶点的最短路径问题时， Floyd 算法应该是不错的选择。