支持向量机手把手实战（进阶版本）
概要
先前我们实现了基础版本的 SVM，现在我们来实现进阶版本。和上次比，这次优化的地方在于：
- 启发式选择参数 alpha（训练速度更快）。通过一个外循环来选择第一个 alpha 值，并且其选择过程中会在两种方式间进行交替：一种方式是在所有数据集上进行单遍扫描，另一种方式则是在非边界（不等于 0 或 C） alpha 中实现单遍扫描。在选择第一个 alpha 值后，算法会通过一个内循环来选择第二个 alpha 值。在优化过程中，会通过最大化步长的方式来获得第二个 alpha 值（Ei-Ej 最大）。
- 引入核函数解决线性不可分的问题。
完整版本的支持向量机
数据集
同样选择机器学习实战中的数据集，可视化如下：
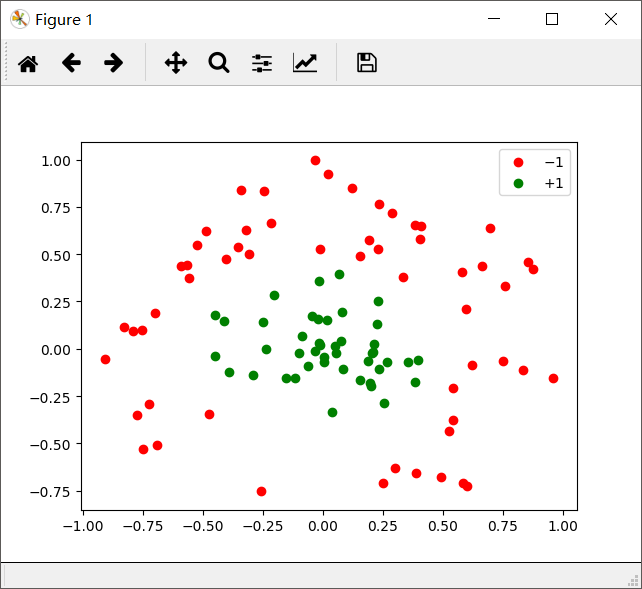
我们使用的是高斯核函数：
\begin{align}
k(x, y) = \mathrm{exp} \left( \frac{-\lVert x-y\rVert 2}{2\sigma2} \right) \notag
\end{align}
其中 \(\sigma>0\) 是用户定义的用于确定到达率或者说函数值跌落到 \(0\) 的速度参数。该函数将数据从其特征空间映射到更高维的空间，具体来说这里是映射到一个无穷维的空间。
如果你成功运行了程序，画出的图像大概长这样：
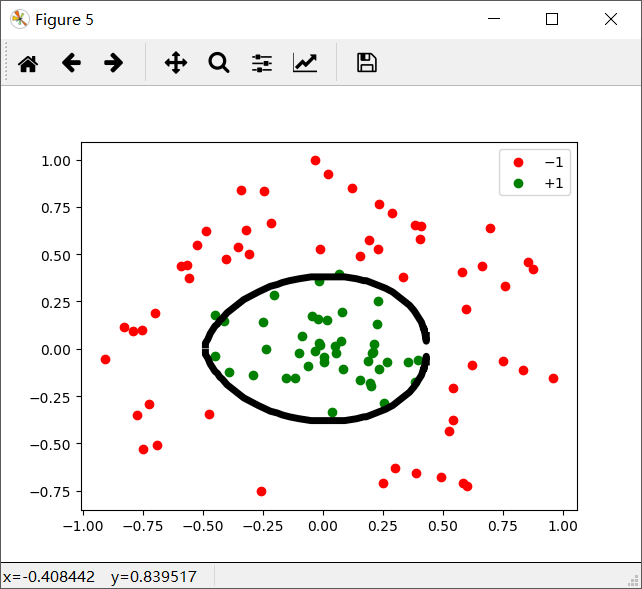
由于一定的随机性，每次画出的图不一样，我选了一张貌似还行的，有的真惨不忍睹，显然算法还有一定的上升空间。
代码
每一步我已经标的很清楚了，不用再啰嗦了，贴代码。
# -*- coding: utf-8 -*-
"""
Created on Mon Apr 2 20:20:20 2018
@author: zhoukui
"""
import numpy as np
import random
import matplotlib.pyplot as plt
def loadData(filename):
dataMat = []
yMat = []
fr = open(filename)
for line in fr.readlines():
line = line.strip().split('\t')
dataMat.append([float(line[0]),float(line[1])])
yMat.append(float(line[2]))
return np.array(dataMat), np.array(yMat) # 大小 (100, 2) , (100,)
def showData(filename, line = None):
dataArr, yArr = loadData(filename)
data_class_1_index = np.where(yArr == -1)
data_class_1 = dataArr[data_class_1_index,:].reshape(-1,2)
data_class_2_index = np.where(yArr == 1)
data_class_2 = dataArr[data_class_2_index,:].reshape(-1,2)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(data_class_1[:,0], data_class_1[:,1], c = 'r', label = "$-1$")
ax.scatter(data_class_2[:,0], data_class_2[:,1], c = 'g', label = "$+1$")
plt.legend()
if line is not None:
b, alphas, kTup = line
#==============================================================================
# for i in range(dataArr.shape[0]): # 画支持向量
# wx = np.sum(alphas*yArr[:,np.newaxis]*kernelTrans(dataArr, dataArr[i,:], kTup)[:,np.newaxis], axis=0)
# y = wx + b
# if (abs(y-1) < 0.1): # +1 类
# ax.scatter(dataArr[i,0], dataArr[i,1], marker='o', s = 90, c = 'black')
# if (abs(y+1) < 0.1): # -1 类
# ax.scatter(dataArr[i,0], dataArr[i,1], marker='o', s = 90, c = 'cyan')
#==============================================================================
# 我想画分界线
points = []
for j in np.arange(0, 0.75, 0.01):
for i in np.arange(-0.75, 0.75, 0.01):
wx = np.sum(alphas*yArr[:,np.newaxis]*kernelTrans(dataArr, np.array([i,j]), kTup)[:,np.newaxis], axis=0)
y = wx + b
if(abs(y-1) < 0.01):
points.append([i,j])
points = np.array(points)
points = points[np.lexsort(points[:,::-1].T)] # 按第一列排序
#print(points)
ax.plot(points[:,0], points[:,1], lw = 5.0 , c = 'black') # 第一二象限
#ax.plot(-points[:,0], points[:,1], c = 'black') # 第二象限
#ax.plot(-points[:,0], -points[:,1], c = 'black') # 第三象限
ax.plot(points[:,0], -points[:,1], lw = 5.0, c = 'black') # 第四象限
plt.show()
def kernelTrans(X, A, kTup):
# 把原先的向量的内积运算，改成核函数运算
# X: 就是样本，shape= (m,n) A: 向量 shape (n,)
# 这里我们封装了两种情况：线性核 'lin'、高斯核 'rbf'
m, n = X.shape
K = np.zeros((m,1))
if kTup[0] == 'lin':
K = np.sum(X*A, axis = 1)
elif kTup[0] == 'rbf':
K = np.sum((X-A)**2, axis = 1)
K = np.exp(K / (-1.*kTup[1]**2)) # kTup[1] 就是参数 sigma
else:
raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
return K
# 构造一个数据结构，方便
class optStruct:
def __init__(self, dataArr, yArr, C, toler, kTup):
self.X = dataArr
self.Y = yArr # 标签
self.C = C
self.tol = toler
self.m = dataArr.shape[0]
self.alphas = np.zeros((self.m, 1))
self.b = 0
# 缓存误差，节省后续的计算时间。第一列给出的是 eCache 是否有效的标志位，值为 0 或 1
# 第二列给出的是实际的 E 值
self.eCache = np.zeros((self.m, 2))
# 构造数组 K, 存储训练过程中所有可能用到的核函数运算，这样后边直接调用就行了
self.K = np.zeros((self.m, self.m))
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
# 计算 fXi 那一个公式，因为后边频繁使用，这里写成函数了
def calcEk(oS, k):
fXk = np.sum(oS.alphas*oS.Y[:,np.newaxis]*oS.K[:,k][:,np.newaxis]) + oS.b
Ek = fXk - oS.Y[k]
return Ek
def selectJrand(i,m):
j=i #we want to select any J not equal to i
while (j==i):
j = int(random.uniform(0,m))
return j
# 内循环的启发式选择方法：依据最大步长确定 alpha
def selectJ(i, oS, Ei):
"""
i :先前确定的第一个 alpha 值下标
Ei : 误差喽
我们要找到一个 j,使得 abs(Ei-Ej) 最大，并返回 j, Ej
"""
maxK = -1 # 这是我们想要的 alpha 下标，先设一个初始值
maxDeltaE = 0 # 差值，先初始化为 0
Ej = 0
# 找到可取的 alpha 值下标列表。这里的“可取”是说明先前的已经计算好了，E 值非 0
# 如果 E 值等于零，那就没必要筛选了，随机选择一个就好，也就是 else 里做的事情
validEcacheList = list(np.nonzero(oS.eCache[:,0])[0]) # 返回不为零的下标,元组形式，所以加[0]得到数组
if (len(validEcacheList) > 1): # 多于一个，选择具有最大的步长
for k in validEcacheList:
if k == i: continue # 当然要选择与 i 不一样的
Ek = calcEk(oS, k)
"""
不能这样写：Ek= oS.eCache[k, 1]， 因为参数 Ek 是在外循环中更新的，看后边的
遍历就可知，外循环一次，内循环可能运行多次，不能及时更新，所以得现算获得最新值
"""
deltaE = abs(Ei-Ek)
if (deltaE > maxDeltaE):
maxK = k
maxDeltaE = deltaE;
Ej = Ek
return maxK, Ej
else: # 如果这是第一次循环，那么缓存中全为 0， 此时就随机选择一个 alpha 值
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
# 计算误差值并存入缓存当中。在对 alpha 值进行优化之后会用到这个值
def updateEk(oS, k):
Ek = calcEk(oS, k)
oS.eCache[k] = [1, Ek] # 1 表示有效的，可取的
# 对 alpha 的修正函数
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
# 内循环
def innerL(i, oS):
"""
内循环要做的就是找到第二个 alpha，然后看情况是否进行优化
最后返回 0 表示 没有进行优化，返回 1 表示进行了优化
"""
# 计算 Ei，也相当于误差
Ei = calcEk(oS, i)
# 同样先判定是否满足优化条件
if( ((oS.Y[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or
((oS.Y[i]*Ei > oS.tol) and (oS.alphas[i] > 0))):
# 到这儿说明满足了优化的条件，启发式选择第二个 alpha
j, Ej = selectJ(i, oS, Ei)
# 更新 alpha 前先复制一下，作为 old
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()
# 计算 L 和 H, alpha 和 L,H 的关系是 0 <= L <= alpha <= H <= C
# 异号的情况, alpha 相减, 否则同号，相加
if( oS.Y[i] != oS.Y[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
# 如果 L == H，那就没什么优化的了，continue
if L == H:
print("L == H")
return 0
# 计算 eta，eta 是 alphas[j] 的最优修改量，如果 eta <= 0，需要退出
# for 循环迭代的过程，实际上是比较边界值，取较小，在此先不处理
#==============================================================================
# eta = np.sum(oS.X[i,:]*oS.X[i,:]) + np.sum(oS.X[j,:]*oS.X[j,:]) - \
# 2. * np.sum(oS.X[i,:]*oS.X[j,:])
#==============================================================================
eta = oS.K[i,i] + oS.K[j,j] - 2.* oS.K[i,j]
if eta <= 0:
print("eta <= 0")
return 0
# 准备好之后，就可以计算出新的 alphas[j] 值
oS.alphas[j] = alphaJold + oS.Y[j]*(Ei-Ej) / eta
# 此时还需要对 alphas[j] 进行修正
oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
# 更新误差缓存
updateEk(oS, j)
# 检查alpha[j]是否只是轻微的改变，如果是的话，就退出for循环
if( abs(oS.alphas[j] - alphaJold) < 0.00001 ):
print("j is not moving enough")
return 0
# 下面对 i 进行修正，修改量与 j 相同，但方向相反
oS.alphas[i] = alphaIold + oS.Y[i]*oS.Y[j]*(alphaJold-oS.alphas[j])
# 更新误差缓存
updateEk(oS, i)
# 下面计算参数 b
bi = oS.b - Ei - oS.Y[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] -\
oS.Y[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
bj = oS.b - Ej - oS.Y[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j] -\
oS.Y[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
# b 的更新条件
if( 0 < oS.alphas[i] and oS.alphas[i] < oS.C):
oS.b = bi
elif( 0 < oS.alphas[j] and oS.alphas[j] < oS.C):
oS.b = bj
else:
oS.b = (bi+bj) / 2.
return 1
else:
return 0
# 外循环
def smoP(dataArr, yArr, C, toler, maxIter, kTup = ('lin', 0)):
"""smoSimple
Args:
dataArr 特征集合
yArr 类别标签
C 松弛变量(常量值)，允许有些数据点可以处于分隔面的错误一侧。
控制最大化间隔和保证大部分的函数间隔小于 1.0 这两个目标的权重。
可以通过调节该参数达到不同的结果。
toler 容错率（是指在某个体系中能减小一些因素或选择对某个系统产生不稳定的概率。）
maxIter 退出前最大的循环次数（alpha 不发生变化时迭代的次数）
Returns:
b 模型的常量值
alphas 拉格朗日乘子
"""
oS = optStruct(dataArr, yArr, C, toler, kTup)
iterations = 0 # 记录迭代次数
entireSet = True # 因为要在非边界循环和完整遍历之间进行切换，所以做个标志
"""
设置一个参数 alphaPairsChanged 记录 alpha 是否已经进行优化，每次循环开始
记为 0，然后对整个集合顺序遍历, 如果没变化，则记为迭代一次
"""
alphaPairsChanged = 0
# 只有在所有数据集上遍历 maxIter 次，且不再发生任何 alpha 修改之后，才退出 while 循环
# 这里的 iteration 与 simple SVM 版本有所不同，这里不管更新没更新 alpha,遍历一次就 +1
while(iterations < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
# 在非边界循环和完整遍历之间进行切换
if entireSet: # 遍历所有值
for i in range(oS.m): # 寻找任意可能的 alpha
alphaPairsChanged += innerL(i, oS) # 记录 alpha 发生变化的次数
print("fullSet, iter: %d , i: %d, pairs changed %d" % (iterations, i, alphaPairsChanged))
iterations += 1
else: # 遍历非边界值，即不在边界 0 或 C 上的值
nonBoundIs = list(np.nonzero((oS.alphas > 0) * (oS.alphas < C))[0])
for i in nonBoundIs:
alphaPairsChanged += innerL(i, oS)
print("non-bound, iter: %d , i: %d, pairs changed %d" % (iterations, i, alphaPairsChanged))
iterations += 1
if entireSet: # 试试加上 and iterations > 200，强制优化
entireSet = False
elif (alphaPairsChanged == 0): # 等于 0 表示没有做什么优化
entireSet = True
print("iteration number: %d" % iterations)
return oS.b, oS.alphas
def testSVM(filename):
dataArr, yArr = loadData(filename)
C = 100
toler = 0.0001
maxIter = 10000
kTup = ('rbf', 1.3)
b, alphas = smoP(dataArr, yArr, C, toler, maxIter, kTup)
showData(filename, line = (b, alphas, kTup))
#return b, alphas
if __name__=="__main__":
testSVM("testSetRBF.txt")
#showData("testSet.txt", line = (b, alphas))
#showData("testSetRBF.txt")
