QR 分解

将学习到什么

介绍了平面旋转矩阵，Householder 矩阵和 QR 分解以入相关性质.

 

---

预备知识

平面旋转与 Householder 矩阵是特殊的酉矩阵，它们在建立某些基本的矩阵分解过程中起着重要的作用。

平面旋转

设 \(1 \leqslant i < j \leqslant n\),称

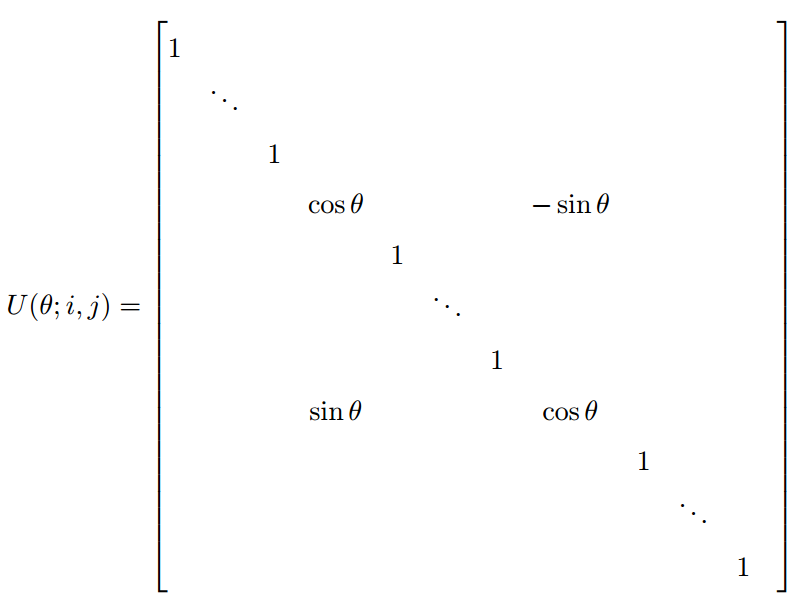
为平面旋转或者 Givens 旋转.

容易验证对任何一对指数 \(i,j,(1 \leqslant i < j \leqslant n)\) 以及任何参数 \(\theta \in [0,2\pi)\), \(U(\theta;i,j) \in M_n(\mathbb{R})\) 都是实正交的. 矩阵 \(U(\theta;i,j)\) 在 \(\mathbb{R}^n\) 的 \(i,j\) 坐标平面上执行一个旋转（旋转任意角度 \(\theta\)）. 用 \(U(\theta;i,j)\) 左乘只影响被乘的矩阵的第 \(i\) 行和第 \(j\) 行，而用 \(U(\theta;i,j)\) 右乘只影响被乘的矩阵的第 \(i\) 列和第 \(j\) 列. 而且 用 \(U(\theta;i,j)^{-1}=U(\theta;i,j)^{T}=U(-\theta;i,j)\).

 

Householder 矩阵

它有几个很好的性质： - 由于 $U_{\omega}^*=I-2(\omega^*\omega)^{-1}(\omega\omega^*)^*=I-2(\omega^*\omega)^{-1}\omega\omega^*=U_{\omega}$, 所以 $U_{\omega}$ 是 Hermite 矩阵. 又由于 $U_{\omega} \cdot U_{\omega}=I$ ，所以 $U_{\omega}$ 是酉矩阵且 $U_{\omega}^{-1}= U_{\omega}$.   - Householder 矩阵 $U_{\omega}$ 在子空间 $\omega^{\perp}$ 上的作用是恒等元，即如果 $x \in \omega^{\perp}$, 就有 $U_{\omega}x=x$.   - Householder 矩阵 $U_{\omega}$ 在子空间 $\mathrm{span}(\omega)$ 上的作用是反射，即 $U_{\omega} \cdot \omega=-\omega$.   - $\mathrm{det}\,U_{\omega}=-1$. 由秩一扰动的行列式公式知 $\mathrm{det}\,U_{\omega}=1-2(\omega^*\omega)^{-1}\omega^* I \cdot \omega=-1$. 由 [Brauer 定理](http://www.cnblogs.com/zhoukui/p/7786648.html)知，它的特征值是 $-1,1,1\cdots$. 于是，对所有 $n$ 以及每个非零的 $\omega \in \mathbb{R}^n$, Householder 矩阵 $U_{\omega} \in M_n(\mathbb{R})$ 是实正交矩阵，但不是**真旋转矩阵**（真旋转矩阵是行列式为 $+1$ 的实正交矩阵）   - 设 $n\geqslant 2$, 并设 $x,y\in \mathbb{R}^n$ 是单位向量. 如果 $x=y$, 令 $\omega$ 是任意一个与 $x$ 正交的实单位向量. 如果 $x \neq y$, 令 $\omega=x-y$. 此时有 $\omega^*\omega=2(1-x^*y),\omega^*x=1-x^*y$, 所以 $U_{\omega}x=y$. 事实上，**任意的 $x\in \mathbb{R}^n$ 可以由实的 Householder 矩阵变换成任何一个满足 $\lVert x\rVert _2=\lVert y\rVert _2$ 的向量 $y \in \mathbb{R}^n$**. 但是在 $\mathbb{C}^n$ 中不一样，不存在 $\omega \in \mathbb{C}^n$ 使得 $U_{\omega} e_1=\mathrm{i}e_1$.

Householder 矩阵以及纯量酉矩阵可以用来构造一个酉矩阵，它将 \(\mathbb{C}^n\) 中任意给定的向量变换成 \(\mathbb{C}^n\) 中有同样 Euclid 范数的另外任意一个向量。

  证明： （A 是本性 Hermite 的是指存在 \(\theta \in \mathbb{R}\) 使 \(\mathrm{e}^{\mathrm{i}\theta}A\) 是 Hermite 的）.

如果 \(x\) 与 \(y\) 线性相关的（也就是说，如果对某个实的 \(\theta\) 有 \(y=\mathrm{e}^{\mathrm{i}\theta}x\)）, 这些结论容易验证. 如果 \(x\) 与 \(y\) 线性无关，由 Cauchy-Schwartz 不等式确保有 \(x^*x\neq \vert x^*y\rvert\). 计算
\begin{align}
\omega^*\omega &=(\mathrm{e}^{{\mathrm{i}\phi}x-y)}*(\mathrm{e}^{{\mathrm{i}\phi}x-y)=x}*x-\mathrm{e}^{{-\mathrm{i}\phi}x}*y-\mathrm{e}^{{\mathrm{i}\phi}y}*x+y^*y \notag \\
&=2(x^{*x-\mathrm{Re}(\mathrm{e}}\phi}x^*y)) \notag \\
&= 2(x^*x-\vert x^*y\rvert) \notag
\end{align}
和
\begin{align}
\omega^*x= \mathrm{e}^{{-\mathrm{i}\phi}x}*x-y^{*x=\mathrm{e}}\phi}x^{*x-\mathrm{e}}\phi}\vert y^{*x\rvert=\mathrm{e}}\phi}(x^*x-\vert x^*y\rvert)) \notag
\end{align}
最后计算
\begin{align}
\mathrm{e}^{{\mathrm{i}\phi}U_{\omega}x=\mathrm{e}}\phi}(x-2(\omega^*\omega)\omega \omega^* x)=\mathrm{e}^{{\mathrm{i}\phi}(x-(\mathrm{e}}\phi}x-y)\mathrm{e}^{-\mathrm{i}\phi})=y \notag
\end{align}
如果 \(z\) 与 \(x\) 正交，那么 \(\omega^*z=-y^*z\), 且
\begin{align}
y^*U(y,x)z &=\mathrm{e}^{\mathrm{i}\phi} \bigg( y^*z-\frac{1}{\lVert x \rVert _2^2-\vert x^*y\rvert)} (\mathrm{e}^{{\mathrm{i}\phi}y}*x-\lVert y \rVert _2^2) (-y^*x) \bigg) \notag \\
&= \mathrm{e}^{\mathrm{i}\phi} ( y^*z+(-y*x))=0 \notag
\end{align}
说明了变换不仅保证了范数不变，还保持了正交不变性. 由于 \(U_{\omega}\) 是酉矩阵，且是 Hermite 矩阵，故而 \(U(y,x)=(\mathrm{e}^{\mathrm{i}\phi}I)U_{\omega}\) 是酉矩阵（它是两个酉矩阵的乘积），且是 Hermite 的.
 
如果 \(y\in\mathbb{C}^n\) 是已知的单位向量，按上述方法构造的 \(U(y,e_1)\) 的第一列肯定是 \(y\), 由于 \(U(y,e_1)\cdot e_1=y\).

 

---

QR 分解

复矩阵或者实矩阵的 QR 分解在理论上与计算上都有相当的重要性.

  证明： 设 \(a_1 \in \mathbb{C}^n\) 是 \(A\) 的第一列，\(r_1=\lVert a_1\rVert_2\), 又设 \(U_1\) 是一个酉矩阵，它使得 \(U_1a_1=r_1e_1\), 上个定理 (1.1) 对这样的矩阵给出了一个明显的构造，它或者是一个纯量的酉矩阵，或者是一个纯量的酉矩阵与一个 Householder 矩阵的乘积. 分划
\begin{align}
U_1A=\begin{bmatrix}
r_1 & \bigstar \\ 0 & A_2
\end{bmatrix} \notag
\end{align}
其中 \(A_2\in M_{n-1,m-1}\). 设 \(a_2\in \mathbb{C}^{n-1}\) 是 \(A_2\) 的第一列，并令 \(r_2=\lVert a_2\rVert_2\). 再次利用定理 (1.1) 来构造一个酉矩阵 \(V_2 \in M_{n-1}\), 使得 \(V_2a_2=r_2e_1\), 再令 \(U_2=I_1\oplus V_2\). 那么
\begin{align}
U_2U_1A=\begin{bmatrix}
r_1 & & \bigstar \\ 0 & r_2 & \\ 0 & 0 & A_3
\end{bmatrix} \notag
\end{align}
重复这一结构 \(m\) 次就得到
\begin{align}
U_mU_{m-1}\cdots U_2U_1A=\begin{bmatrix}
R \\ 0
\end{bmatrix} \notag
\end{align}
其中 \(R\in M_m\) 是上三角的，其主对角元素是 \(r_1,\cdots,r_m\), 它们全都是非负的. 设 \(U=U_mU_{m-1}\cdots U_2U_1\). 分划 \(U^*=U_1^*U_2^*\cdots U_{m-1}^*U_m^*=[Q\quad Q_2]\), 其中 \(Q \in M_{n,m}\) 的列是标准正交的（它包含了一个酉矩阵的前 \(m\) 个列）. 这样就有 \(A=QR\). 如所希望的那样. 如果 \(A\) 是列满秩的，则 \(R\) 是非奇异的，所以它的主对角线元素全是正的.
假设 \(\mathrm{rank}\, A=m\), 且 \(A=QR=\tilde{Q}\tilde{R}\), 其中 \(R\) 与 \(\tilde{R}\) 是上三角的且有正的主对角元素，而 \(Q\) 与 \(\tilde{Q}\) 都标准正交的列向量. 那么 \(A^*A=R^*(Q^*Q)R)=R^*IR=R^*R\), 且还有 \(A^*A=\tilde{R}^*\tilde{R}\), 所以 \(R^*R=\tilde{R}^*\tilde{R}\) 且 \(\tilde{R}^{-*}R^*=\tilde{R}R^{-1}\). 也就是说下三角阵等于一个上三角矩阵，所以它们两者必定都是对角矩阵：\(\tilde{R}R^{-1}=D\) 是对角的，且它必定有正的主对角元素，这是因为 \(\tilde{R}\) 与 \(R^{-1}\) 这两者的主对角元素都是正的. 但是 \(\tilde{R}=DR\) 蕴含 \(D=\tilde{R}R^{-1}=\tilde{R}^{-*}R^*=(DR)^{-*}R^*=D^{-1}R^{-*}R^*=D^{-1}\), 所以 \(D^2=I\), 从而 \(D=I\). 所以有 \(\tilde{R}=R\) 以及 \(\tilde{Q}=Q\).
(c) 中的结论由列向量标准正交的方阵是酉矩阵这一事实推出.
如果 (d) 中有 \(n \geqslant m\), 我们可以从 (a) 中的分解开始，设 \(\tilde{Q}=[Q\quad Q_2] \in M_n\) 是酉矩阵，令 \(\tilde{R}=\begin{bmatrix} R \\ 0 \end{bmatrix} \in M_{n,m}\), 并注意到 \(A=QR=\tilde{Q}\tilde{R}\). 如果 \(n<m\), 我们就可以采用 (a) 中的构造（用 Householder 变换的一列纯量倍数左乘）并在 \(n\) 步后停止，这时就得到分解式 \(U_n\cdots U_1A=[R\quad \bigstar]\), 而 \(R\) 是上三角的. \(\bigstar\) 这个块中的元素不一定为零.
最后的结论 (e) 从定理 (1.1) 中的如下结论推出：(a) 与 (d) 的结构中所包含的酉矩阵 \(U_i\) 可以全部取为实矩阵.
 
任何形如 \(B=A^*A\) 的 \(B\in M_n(A\in M_n)\) 可以写成 \(B=LL^*\), 其中 \(L \in M_n\) 是下三角矩阵，且有非负的对角元素. 如果 \(A\) 是非奇异的，这个分解是唯一的. 其实这是 \(B\) 的 Cholesky 分解，每一个正定的或半正定的矩阵都可以用这种方式进行分解.
\(A\in M_{n,m}\) 的 QR 分解得到的变量有时很有用. 假设 \(n \leqslant m\), 并令 \(A^*=QR\), 其中 \(Q \in M_{n,m}\) 有标准正交的列，而 \(R\in M_m\) 是上三角的. 这样，\(A=R^*Q^*\) 就是形如
\begin{align}
A=LQ
\end{align}
的一个分解，其中 \(Q\in M_{n,m}\) 有标准正交的行，且 \(L\in M_n\) 是下三角的. 如果 \(\tilde{Q}=\begin{bmatrix} Q \\ \tilde{Q}_2 \end{bmatrix}\) 是酉矩阵，我们就有形如
\begin{align}
A=\begin{bmatrix} L & 0 \end{bmatrix} \tilde{Q}
\end{align}
的分解.

我们举个例子，对矩阵 \(A=\begin{bmatrix} 1 & 1 & 1 \\ 2 & -1 & -1 \\ 2 & -4 & 5 \end{bmatrix}\) 进行 QR 分解. 按照上述证明过程，先拿出矩阵 \(A\) 的第一列 \(a_1=[1,2,3]^T\)，求出 \(\lVert a_1 \rVert_2=3\)，现在要求一个酉矩阵 \(U_1\) 使得 \(U_1a_1=3e_1\). 按照定理 1 计算 \(a_1^*\cdot 3e_1=3\) 是正号，所以 \(w=a_1-3e_1=[-2,2,2]^T\). 归一化得 \(w=[-1/\sqrt{3},1/\sqrt{3},1/\sqrt{3}]^T\), 计算酉矩阵 \(U_1=I-2ww^*=\frac{1}{3}\begin{bmatrix} 1 & 2 & 2 \\ 2 & 1 & -2 \\ 2 & -2 & 1 \end{bmatrix}\), 计算 \(U_1A=\begin{bmatrix} 3 & -3 & -3 \\ 0 & 3 & -3 \\ 0 & 0 & 3 \end{bmatrix}=R\). 我们运气比较好，直接变成上三角了，否则重复上述步骤，此时就完成了 QR 分解，由于是实数域，故 \(U_1^{-1}=U_1^T\), 所以 \(A=U_1^TR\).

一个重要的几何事实是：任何两个有相同个数的标准正交向量组都通过酉变换联系在一起.

  证明： 将标准正交向量 \([x_1 \,\,\cdots \,\,x_k]\) 与 \(Y=[y_1 \,\,\cdots \,\,y_k]\) 中的每一个都通过 Gram-Schmidt 扩充为 \(\mathbb{C}^n\) 的一组标准正交基，也就是构造酉矩阵 \(V=[X\quad X_2]\) 以及 \(W=[Y\quad Y_2]\in M_n\). 那么 \(U=WV^*\) 是酉矩阵，且 \([Y\quad Y_2]=W=UV=[UX \quad UX_2]\), 所以 \(Y=UX\). 如果 \(X\) 与 \(Y\) 是实的，则矩阵 \([X\quad X_2]\) 与 \([Y\quad Y_2]\) 可以选为实的正交矩阵（它们的列是 \(\mathbb{R}^n\) 的标准正交基）.

 

---

读完应该知道什么

• 平面旋转与 Householder 矩阵是特殊的酉矩阵
• Householder 矩阵的特征值是 \(-1,1,1\cdots\), 所以其行列式为 -1
• Householder 矩阵以及纯量酉矩阵可以用来构造一个酉矩阵，它将 \(\mathbb{C}^n\) 中任意给定的向量变换成 \(\mathbb{C}^n\) 中有同样 Euclid 范数的另外任意一个向量。
• QR 分解