动态规划 002 -数字三角形问题

问题描述

下图给出了一个数字三角形，请编写一个程序，计算从顶至底的某处的一条路径，使该路径所经过的数字的总和最大。
（1）每一步可沿左斜线向下或右斜线向下
（2）1 < 三角形行数 < 100
（3）三角形数字为0，1，…99之间

输入

第1行是输入整数，表示三角形行数n，然后是n行数

输出描述

输出最大值。

样例输入

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

样例输出

30

---

递归解法

解题思路

用二维数组存放数字三角形。 D( r, j) : 第r行第 j 个数字(r,j从1 开始算) MaxSum(r, j) :
从D(r,j)到底边的各条路径中，最佳路径的数字之和。
问题：求 MaxSum(1,1)
这是典型的递归问题。

D(r, j)出发，下一步只能走D(r+1,j)或者D(r+1, j+1)。
即MaxSum( r, j) = Max{ MaxSum(r＋1,j), MaxSum(r+1,j+1) } + D(r,j);
故对于N行的三角形：

if ( r == N)
    MaxSum(r,j) = D(r,j);
else
    MaxSum( r, j) = Max{ MaxSum(r＋1,j), MaxSum(r+1,j+1) } + D(r,j);

代码实现

#include <iostream>
#include <algorithm>
#define Max 101
using namespace std;

int D[Max][Max];
int num;
int MaxSum(int i, int j){
    if(i == num)
        return D[i][j];
    int x = MaxSum(i + 1, j);
    int y = MaxSum(i + 1, j + 1);
    return max(x,y) + D[i][j];
}

int main(int argc, char const *argv[])
{
    int i, j;
    cin >> num;
    for(i = 1; i <= num; i ++)
        for(j = 1; j <= i; j ++)
            cin >> D[i][j];
    cout << MaxSum(1,1) << endl;
    return 0;
}

时间复杂度

递归求解，会严重超时，因为出现大量重复计算，如下图所示。深度遍历每条路径，存在大量重复计算。5行的总时间为：1+2+4+8+16=31=2^5−1，则时间复杂度为 2^n。

---

记忆型动态规划

这种方法仍有优化的余地，也就是下面第三种思路，表格记录每次计算子问题的数据。

解题思路

第一次计算MaxSum(r,j)值的时候，保存下来，下次需要的时候，直接取出计算，这样就避免了重复计算。时间复杂度为O(n^2)，因为三角形的数字总和为n(n+1)/2。

代码实现

#include <iostream>
#include <algorithm>
#include "string.h"
#define Max 101
using namespace std;
int D[Max][Max];
int Max_Sum_arr[Max][Max];
int num;
int MaxSum(int i, int j){
    if(Max_Sum_arr[i][j] != -1)
        return Max_Sum_arr[i][j];
    if(i == num)
        Max_Sum_arr[i][j] = D[i][j];
    else{
        int x = MaxSum(i + 1, j);
        int y = MaxSum(i + 1, j + 1);
        Max_Sum_arr[i][j] = max(x,y) + D[i][j];
    }
    return Max_Sum_arr[i][j];
}
int main(int argc, char const *argv[])
{
    int i, j;
    cin >> num;
    for(i = 1; i <= num; i ++)
        for(j = 1; j <= i; j ++)
            cin >> D[i][j];
    memset(Max_Sum_arr,-1,sizeof(Max_Sum_arr));
    cout << MaxSum(1,1) << endl;
    return 0;
}

---

递推型动态规划

表格记录子问题数据

解题思路

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

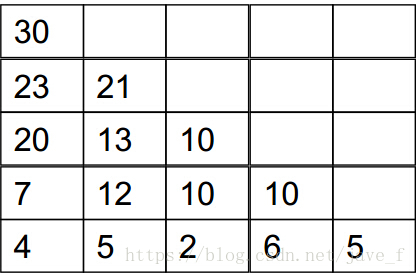
从底向上递推，出最后一行外，每一行的每个点的最大值等于自身加上下面一行对应左右两个点的最大值，从下往上递推，最顶部的即所求。比如下图所示。首先最后一行的最大值就是它本身。倒数第二行第一个数7就是输入的倒二行的第一个数2 + 4 和 2 +5 取最大值 。逐步递推到顶部。

代码实现

#include <iostream>
#include <algorithm>
#include "string.h"
#define Max 101
using namespace std;
int D[Max][Max];
int num;
int MaxSum(int num){
    int i, j;
    for(i = num - 1; i >= 1; i --)
        for(j = 1; j <= i; j ++){
            D[i][j] = max(D[i+1][j],D[i+1][j+1]) + D[i][j];
        }
    return D[1][1];
}
int main(int argc, char const *argv[])
{
    int i, j;
    cin >> num;
    for(i = 1; i <= num; i ++)
        for(j = 1; j <= i; j ++)
            cin >> D[i][j];
    cout << MaxSum(num) << endl;
    return 0;
}

本文转载自：
https://blog.csdn.net/zwhlxl/article/details/46225947
https://www.cnblogs.com/jacklovelol/p/6014059.html

【附：一文一图】