线段树

线段树的概念

线段树类似于区间树，是一个完全二叉树。它在各个节点保存一条线段，主要用于解决高效连续区间的动态查询问题，由于二叉树结构的特性，它基本能保持每个操作的时间复杂度为O(logn),线段树支持区间求和，区间最大值，区间修改，单点修改等等。

线段树的原理及其实现

线段树主要是把一段大区间平均划分成两段小区间进行维护，再用小区间的值来更新大区间。这样既能保证正确性，又能保持时间在logn级别（因为这课线段树是平衡的）。也就是说，一个[L.R]的区间会被划分[L, mid]和[mid+1,R]这两个小区间进行维护，知道L = R。

下图就是一颗[1,6]的线段树分解过程，每一个节点保存了信息。

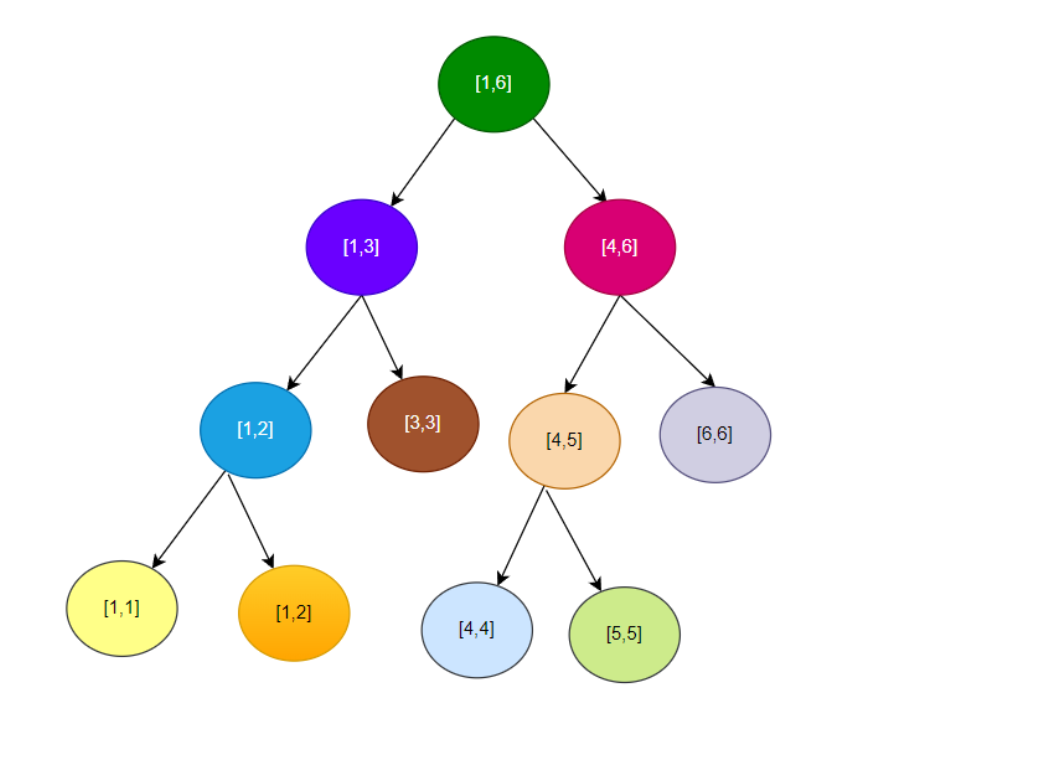
存储方式

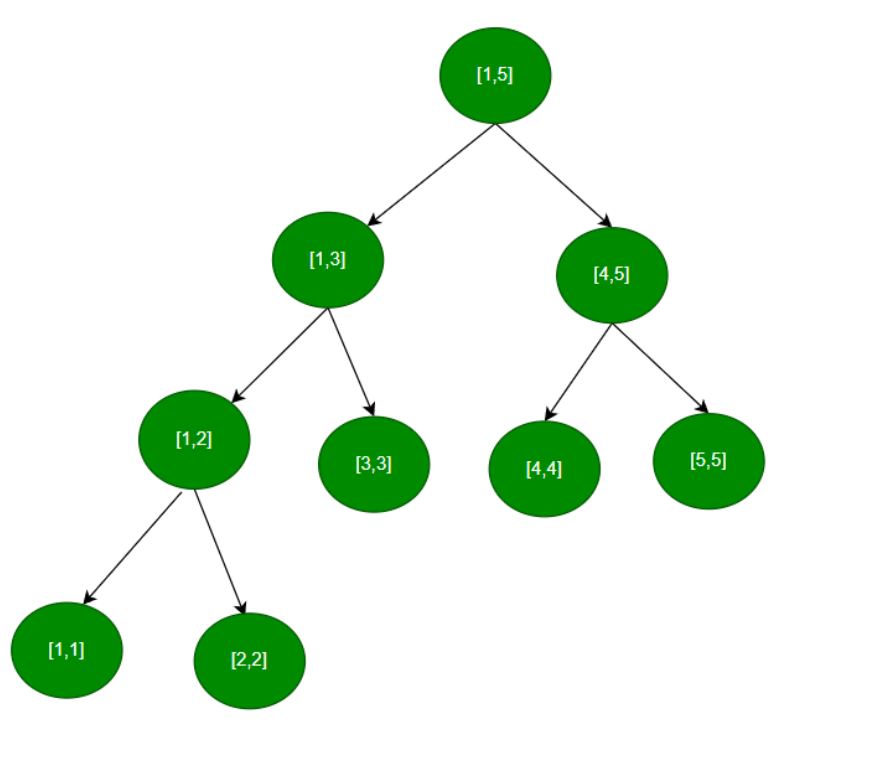
用数组来存储节点，为了方便起见数组下标为1开始，假设任何节点为i,它的父节点的下标为i/2,它的左孩子节点为2i,它的右孩子节点为2 * i +1，假设原数组的长度为N,最省的情况下长度为2的某次幂，只需要2N的长度，最浪费的情况下长度为2的某次幂加1准备4N就够用了，所以浪费一点点空间准备4N的空间。

例如有一个长度为5的数组。根据二叉树的特性最后一层的节点数量约等于上面所有层节点之和，上面的节点为2N,则最后一层的节点也为2N,所以总节点数量为4N.

线段树的例子

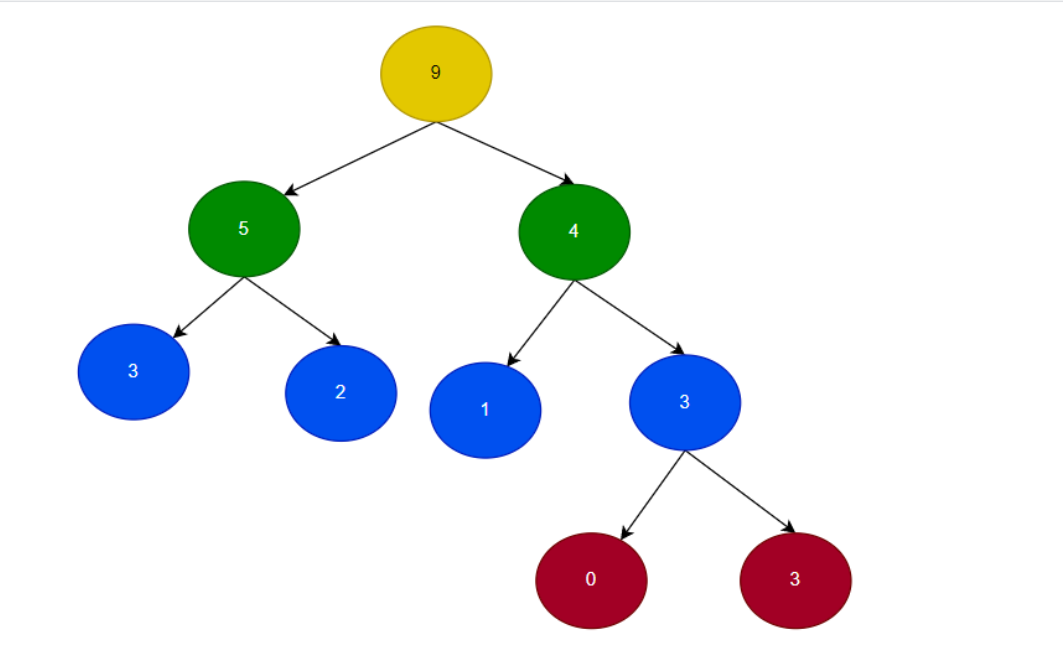
举个线段树的例子，数组为arr=[3,2,1,0,3],组成线段树如图所示，第一个节点为9，代表的是1-5范围上的和，第二个节点是5代表的是1-2范围上数的和，第三个节点的和为4代表的是3-5上的和，依次类推。

引入懒更新

当某个区间要进行更新时，可以把这个更新存在layz数组里面，等需要用的时候再来进行发放更新，这就是所谓的懒功能，举个例子：比如数组为1-5，在1-5上加上2，就把layz[1]置为2，当要查询1-5下面的子节点的时候，在进行发放更新，这就节省了时间。

初始化

public static class SegmentTrees{
        //arr[]为原序列的信息从0开始，但在arr里是从1开始的
        //sum[]模拟线段树维护区间和
        //lazt[]为累加和懒惰标记
        //change[]为更新的值
        //update[]为更新懒惰标记
        private int MAXN;
        private int[] arr;
        private int[] sum;
        private int[] lazy;
        private int[] change;
        private boolean[] update
public SegmentTrees(int[] orgin){
    //因为从1开始，所以长度应该大1
     MAXN = orgin.length + 1 ;
     arr = new int[MAXN];
    for (int i = 1 ; i < MAXN ; i++){
    	arr[i] = orgin[i - 1];
    }
    //四倍绝对够用了
    sum = new int[MAXN << 2];//用来脑补概念，某一个范围累加和的信息
    lazy = new int[MAXN << 2];//用来脑补概念，某一个范围没有往下的叠加任务
    change = new int[MAXN << 2];//用来支持脑部概念中，某一个范围有没有更新操作的任务
    update = new boolean[MAXN << 2];//用来支持脑补概念中，某一个范围更新任务，更新成什么
}

原始值准备

L到R范围上的所有划分出的范围你该填好就填好，函数传入的值就是下标。

public void build(int l , int r ,int rt){
    if(l == r){
        sum[rt] = arr[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(l,mid,rt<<1);
    build(mid + 1,r,rt << 1 | 1);
    pushUp(rt);
}
private void pushUp(int rt){
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}

add方法

private void add(int L , int R , int l ,int r ,int C ,int rt){
	if (L <= l && R >= r){
     	sum[rt] += C * (r - l + 1);
        lazy[rt] += C;
        return;
    }
   //任务没有全包
   int mid =(l + r) >> 1;
   pushDown(rt,mid - l + 1 , r - mid + 1);
   //L - R
   //总任务需要发给左边
   if (L <= mid){
   add(L , R , l , mid , C ,rt * 2);}
   //总任务需要发给右边
   if (R > mid){
    add(L , R ,mid + 1 ,r ,C , rt * 2 + 1);}
    //当左边发完右边发完了，
    PushUp(rt);}

update方法

//L-R所有的值都变成C
//l -r rt
private void update(int L ,int R ,int C ,int l,int r,int rt) {
	if (L <= l && R >= r) {
		update[rt] = true;
         change[rt] = C;
         sum[rt] = C * (r - l + 1);
         lazy[rt] = 0;
         return;}
//当前任务躲不掉
     int mid = (l + r) >> 1;
     pushDown(rt, mid - l + 1, r - mid);
     if (L <= mid) {
     	update(L, R, C, l, mid, rt * 2);
     }
     if (mid < R) {
     	update(L, R, C, mid + 1, r, rt * 2 + 1);
      }
      PushUp(rt);
}
//ln表示左子树元素节点个数，rn表示右子树节点个数
private void pushDown(int rt , int ln ,int rn){
	if (update[rt]){
     	update[rt * 2] = true;
        update[rt * 2 + 1] = true;
        change[rt * 2] = change[rt];
        change[rt * 2 + 1] = change[rt];
        lazy[rt * 2] = 0 ;
        lazy[rt * 2 + 1] = 0 ;
        sum[rt * 2] = change[rt] * ln;
        sum[rt * 2 + 1] = change[rt] *rn;
        update[rt] = false;
      }
    //只发一层
     if (lazy[rt]!=0){
     	lazy[rt * 2] += lazy[rt];
        sum[rt * 2]+= ln * lazy[rt];
        lazy[rt * 2 + 1] += lazy[rt];
        sum[rt * 2 + 1] = rn * lazy[rt];
        lazy[rt] = 0;}
}

query方法

//查询
private long query(int L ,int R ,int l , int r ,int rt){
//如果任务是全挡着的直接告诉这个累加和就可以了
	if (L <= l && r <= R){
     	return sum[rt];
    }
    int mid = (l + r) >> 1;
    pushDown(rt,mid - l + 1 ,r -mid);
    long ans = 0 ;
    if (L <= mid){
    	ans += query(L , R , l,mid ,rt * 2);}
    if (R > mid){
   		ans += query(L , R , mid +1 ,r ,rt * 2 + 1);}
   return ans; 
	}
}