时间复杂度

时间复杂度是衡量算法好坏的一个重要指标。

 

衡量代码好坏，包括两个非常重要的指标：

 

1、运行时间；

2、占用空间；

 

由于运行环境和输入规模的影响，代码的绝对执行时间是无法评估的，但我们却可以预估代码基本操作执行次数。

 

基本操作次数

 

场景一：一条长10寸的面包，每3天吃掉1寸，那么吃掉整个面包需要几天？

 

答案是3 * 10 = 30天。如果面包的长度是N寸呢？此时吃掉整个面包，需要3 * n = 3n。如果用一个函数来表达这个相对时间，可以记作T（n） = 3n。

 

执行次数是线性的。

 

场景二：一条长16寸的面包，每5天吃掉剩余面包剩余长度的一半，第一次吃掉8寸，第二次吃掉4寸，第三次吃掉2寸…….那么把面包吃得只剩1寸，需要多少天？

 

这个问题翻译一下，就是数字16不断地除以2，除第几次以后的结果等于1？这里涉及到数字当中对数，以2为底，16的对数，可以简写log16。因此，把面包吃得只剩1寸，需要5 * log16 = 5 *  4 = 20天。如果面包的长度是N寸呢？需要5 * logn = 5logn，记作T（n） = 5logn。

 

执行次数是对数的。

 

场景三：一条长10寸的面包和一个鸡腿，每2天吃掉一个鸡腿。那么吃掉整个鸡腿需要多少天呢？

 

答案自然是2天。因为吃说吃掉鸡腿，和10寸的面包没有关系。如果面包的长度是N寸呢？无论面包有多长，吃掉鸡腿的时间仍然是2天，记作T（n） = 2。

 

执行次数是常量的。

 

场景四：一条10寸的面包，吃掉第一个1寸需要1天时间，吃掉第二个1寸需要2天时间，吃掉第三个1寸需要3天时间……每多吃一寸，所花的时间也多1天，那么吃掉整个面包需要多少天呢？

 

答案是从1累加到10的总和，也就是55天。如果面包的长度是N呢？此时吃掉整个面包，需要1+2+3+….+n-1+n = (1+2)*n/2 = 0.5n^2 + 0.5n，记作T（n） = 0.5n^2 + 0.5n。

 

执行次数是一个多项式

 

渐进时间复杂度

 

有了基本操作的执行次数函数T（n），是否就可以分析和比较一段代码的运行时间了呢？还是有一定困难的。

 

比如算法A的相对时间是T（n） = 100n，算法B的相对时间是T（n） = 5n^2，这两个到底谁运行时间更长一些？这就要看n的取值了。

 

所以，这个时候有了渐进时间复杂度的概念，官方的定义如下：

若存在函数f（n），使得当n趋近于无穷大时，T（n） / f（n）的极限值为不等于0的常数，则称f（n）是T（n）的同数量级函数。

 

记作T（n） = O（f（n）），称O（f（n））为算法的渐进时间复杂度，简称时间复杂度。

 

渐进时间复杂度用大写O来表示，所以也被称为大O表示法。

 

如何推导出时间复杂度呢？有如下几个原则：

 

1、如果运行时间是常数量级，用常数1表示；

 

2、只保留时间函数中的最高阶项；

 

3、如果最高阶项存在，则省去最高阶项前面的系数；

 

场景一：T（n） = 3n，最高阶项为3n，省去系数3，转化的时间复杂度为：T（n） = O（n）。

 

场景二：T（n） = 5logn，最高阶项为5logn，省去系数5，转化为时间复杂度为：T（n） = O（logn）。

 

场景三：T（n） = 2，只有常数量级，转化为时间复杂度为：T（n） = O（1）。

 

场景四：T（n） = 0.5n^2 + 0.5n，最高阶项为0.5n^2，省去系数0.5，转化为时间复杂度为：T（n） = O（n^2）。

 

这四种时间复杂度究竟谁用时更长，谁更省时间呢？稍微思考一下就可以得出结论：

 

O（1）< O（logn）< O（n） < O（n^2）

 

现在计算机硬件性能越来越强，为什么还重视时间复杂度呢？

 

我们来举个例子：

 

1、算法A的相对时间规模是T（n） = 100n，时间复杂度是O（n）；

 

2、算法B的相对时间规模是T（n） = 5n^2，时间复杂度是O（n^2）；

 

算法A运行在家里的老旧电脑上，算法B运行在某台超级计算机上，运行速度是老旧电脑的100倍。

 

那么，随着输入规模n的增长，两种算法谁运行更快呢？

 

 

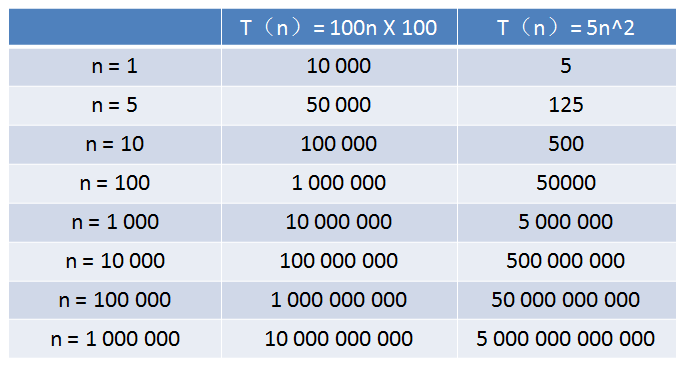
从表格中可以看出，当n的值很小的时候，算法A的运行用时要远大于算法B；当n的值达到1000左右，算法A和算法B的运行时间已经很接近；当n的值越来越大，达到十万、百万时，算法A的优势开始显现，算法B则越累越慢，差距越来越明显。