卡尔曼滤波

 

假设我养了一只猪：

 

一周前，这只猪的体重是46±0.5kg。注意，在这里我用了±0.5，表示其实我对这只猪一周前的体重并不是那么确定的，也就是说，46kg这个体重有0.5kg的误差。
现在，我又养了这只猪一个星期。那么我想要知道它一个星期之后多重，又大概有多少的误差？

 

 为了得到一周后的体重，我有两种方法：一是根据我多年的养猪经验得到的猪体重公式推求出一个大概的值，另一个就是直接去称它的体重。当然，两种方法都有一定的误差。假设经验公式得到的体重是48kg，误差2kg；直接称体重得到的是49kg，误差1kg：

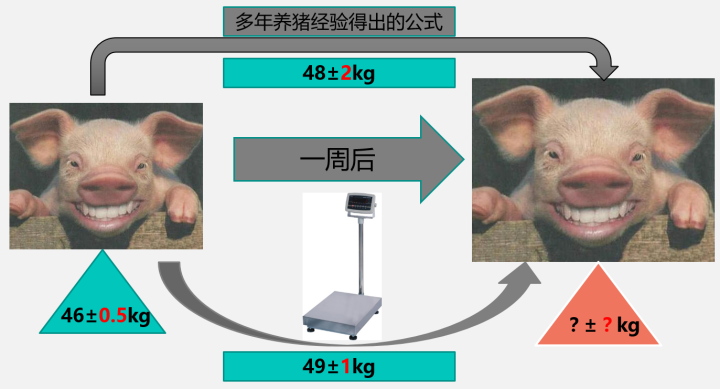
可是，我是一个处女座的人，不管是经验公式得到的值，还是直接称量得到的值，我都觉得不够准。我希望有一种方法，可以同时结合这只猪一周前的体重、用经验公式估计的值以及直接称量得到的值，综合考虑，得出一个最接近猪真实体重的，误差最小的值。这就是卡尔曼滤波要完成的任务。
现在我们来把养猪的模型抽象成数学公式：

 

 

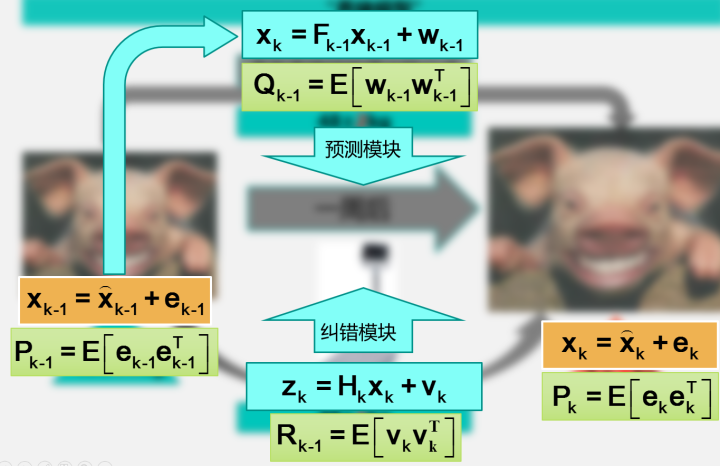
上图的左边，上一周的猪的体重，可以抽象为也k-1时刻的状态值，用k-1时刻的最优估计值加上一个误差项来表示，右边同理。其中，

这一项表示的是估计值的协方差。这里要说明两点：1，上图中所有的变量都是用粗体，表示这是一个向量或者一个矩阵；2，之所以用（列）向量而非一个数来表示状态值，是因为，虽然一只猪的体重可以用一个值来表示，但是在实际的应用中很多状态并不是一个数就能表示的（比如导弹在空间中的位置，同时有x、y、z三个坐标）。
上图中右边表示k时刻的状态值，这个值可以通过预测模块（也就是根据经验公式估计猪的体重）和纠错模块（也就是直接去称量猪的体重值）来估计。同样，预测模块和纠错模块都有着对应的误差和误差协方差矩阵。卡尔曼滤波要做的，就是根据贝叶斯估计的相关理论，同时考虑预测模块和纠错模块的协方差，对误差小的项赋予较大的权重，对误差大的项赋予较小的权重，并使预测的误差最小。

 

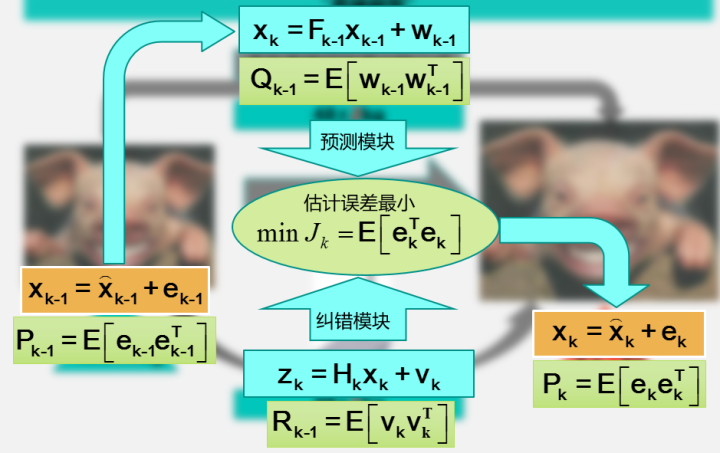
具体的实现过程如下：

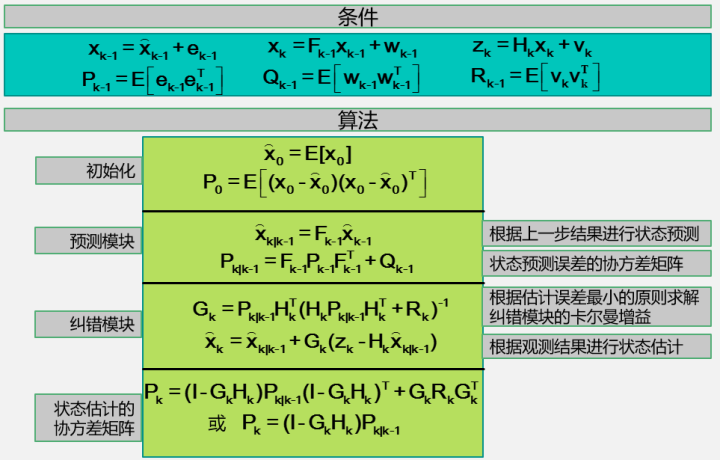
至于具体的这个过程是怎么推求的，每个参数的详细解释又是怎么样的，这个在所有介绍卡尔曼的滤波的书上都有讲述，也并不是一个帖子就能说清楚的，这里就不展开讲了~
谢谢各位看官~