并查集
并查集是一种非常灵活的数据结构,他是用来处理一些不相交的集合问题,如求最小的团伙数,连通子图等等。
在使用并查集的时候,首先会存在一些不相交的动态集合,s{s1,s2......},一般集合中的元素是会用整数来表示。
并查集一般包含以下几个部分。
1:设置每一个元素的父节点为自身。
2:find()函数:查找某一个元素所在集合的代表元素。
3:merge()函数:将一个新的元素合并到一个集合中去。

int father[100000];//具体大小可以自己定。
for(int i=1;i<=100000;i++)
father[i]=i;//初始化每一个元素的父节点是自己本身。

从上面这个图片我们可以看到一棵树的每一个节点都指向他的父节点,根节点指向自己。这个就是我们如何用集合中的某一个元素可以查找到这个集合的代表元素方法,通过找这个元素的的父节点,如果这个元素的父节点不是他本身,那么我们就要接着找这个元素的父节点的父节点,直到找到某个元素的的父节点是他本身,那么这个元素就是这个集合的代表元素。
int find(root)
{
while(root!=father[root])
root=father[root];
return root;
}
这样的查找方式就是每一次查找元素的父节点,直到查找到某个元素的父节点是自己本身,那么这个元素就是这个集合的代表元素。但是这样的查找方式非常的费时间,这样就引申出了路径压缩问题。

可以看出如果我们将集合中的每一个元素都指向这个代表元素的,就不用做太多的查找,这就是路径优化。
int find(root)
{
if(root!=father[root]) father[root]=find(father[root]);
return father[root];
}
现在我们可以查找到每一个集合的代表元素,那么我们怎样将一个新增的元素合并到这个集合呢?我们只需要将新增的这个元素的父节点设置为这个集合的代表元素就可以了。
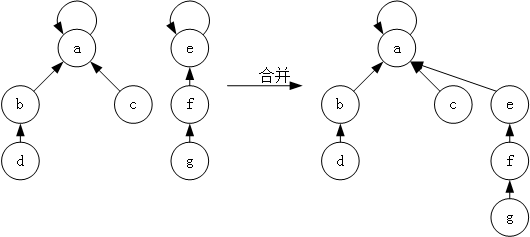
void merge(int a,int b)
{
int aa=find(a);//找到a所在集合的代表元素
int bb=find(b);//找到b所在集合的代表元素
if(aa!=bb) father[b]=a//如果他们的代表元素不一样,将b的父节点设为a。
}
例题:https://www.luogu.org/problem/P1892
AC代码:

#include<iostream> using namespace std; int father[10000],pe[10000]; int find(int root) { while(root!=father[root]) root=father[root]; return root; } void merge(int a,int b) { int aa=find(a); int bb=find(b); if(aa!=bb) father[b]=a; } int main() { int N; cin>>N; for(int i=1;i<=N;i++) father[i]=i; int n; cin>>n; for(int i=1;i<=n;i++) { int re; int a,b; cin>>re>>a>>b; if(re=='F') merge(a,b); else { if(pe[a]==0) pe[a]=find(b); else merge(pe[a],b); if(pe[b]==0) pe[b]=find(a); else merge(pe[b],a); } } int ans=N; for(int i=1;i<=N;i++) if(father[i]!=i) ans--; cout<<ans; return 0; }



