归并排序+典型例题（逆序对）

归并排序用的是分治的思想。分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。即一种分目标完成程序算法，简单问题可用二分法完成。

这里的归并排序就是将一个序列分成多个序列，可分成每个序列只有一个元素，然后将挨着的两个区间的元素进行对比，然后排序。

我们可以用递归来完成这个分区间的步骤，直至每个区间只有一个元素，将左右区间的每个元素进行比较，较小的存放进辅助数组。

大致步骤：（记作左区间的指针为i，右区间的指针为j）

1：建立辅助数组。

2：分区间（递归完成）

3：比较左右区间的的第一个值，如果左区间的较小，存入辅助数组，i++，如果右区间的数较小，存入辅助数组，j++，直到i=mid或者j=end。

4：将左区间或者右区间剩余的数存入到辅助数组中去（由于到了i=mid||j=mid的时候我们就不在比较了，所以会存在左区间的数或者右区间的数没有全部存入辅助数组中去。）

5：将辅助数组中的数存入原数组中去。

图解：

 

由图我们可以看到起始数组为：{80,30,60，40，20,10,,50,70}，

经过分解之后我们分成了8个数组：{80}，{30}，{60}，{40}，{20}，{10}，{50}，{70}。

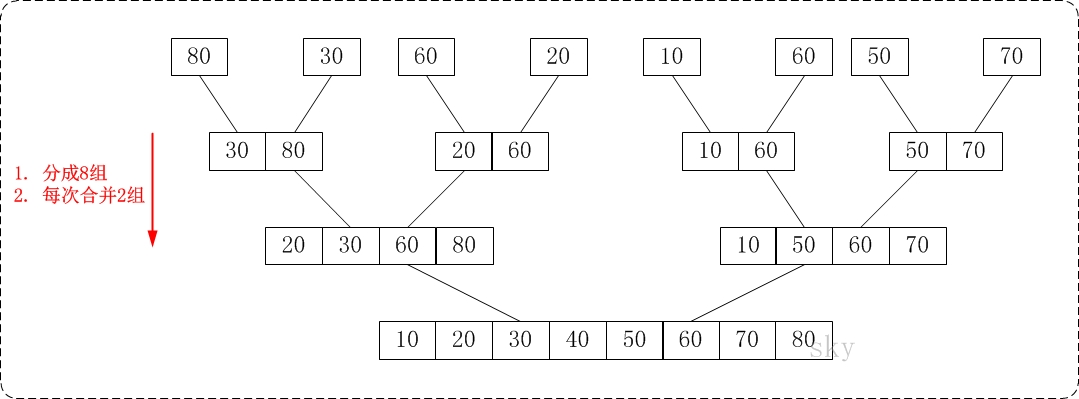
分解之后自然要合并：

第一步我们可以看到都是单个元素在比较大小，小的先存入到辅助数组。

第二步就是两个区间在进行比较了，就要之前将到的比较大小的方法来讲区间中的每个数存入到辅助数组中去。

代码：

 

#include<iostream>
using namespace std;
int B[100000];//辅助数组 
void m_sort(int A[],int start,int end)
{
    if(start==end) return ;
    int mid=(start+end)/2;
    m_sort(A,start,mid);//分左边区间 
    m_sort(A,mid+1,end);//分右边区间 
    int i=start,j=mid+1,k=start;
    while(i<=mid&&j<=end)//左右区间的数作比较，较小的放在辅助数组的前面 
    {
        if(A[i]<=A[j])  
        {
            B[k]=A[i];
            k++;
            i++;
        }
        else 
        {
            B[k]=A[j];
            j++;
            k++;
        }    
    }
    while(i<=mid)//将左边剩余的放在辅助数组 
        {
            B[k]=A[i];
            i++;
            k++;
        }
        while(j<=end)//将右边区间剩余的放在辅助数组 
        {
            B[k]=A[j];
            k++;
            j++;
        }
        for(int t=start;t<=end;t++)//存放进A数组 
           A[t]=B[t];    
}
int main()
{
    int n;
    cin>>n;
    int A[n];
    for(int i=0;i<n;i++)
      cin>>A[i];
    m_sort(A,0,n-1);
    for(int i=0;i<n;i++)
      cout<<A[i]<<" ";
     return 0; 
}

 

 逆序对例题：

题目链接：https://www.luogu.org/problem/P1908

代码：

#include<iostream>
using namespace std;
int B[1000000];
long long ans=0;
void m_sort(int A[],int s,int t)
{
    if(s==t) return ;
    int mid=(s+t)/2;
    m_sort(A,s,mid);
    m_sort(A,mid+1,t);
    int i=s,j=mid+1;
    int k=s;
    while(i<=mid&&j<=t)
    {
        if(A[i]<=A[j])
        {
            B[k]=A[i];
            i++;
            k++;
        }
        else 
        {
            ans+=mid+1-i;//在此找逆序对， 
            B[k]=A[j];
            j++;
            k++;
        }
    }
    while(i<=mid)
    {
        B[k]=A[i];
        i++;
        k++;
    }
    while(j<=t)
    {
        B[k]=A[j];
        j++;
        k++;
    }
    for(int i=s;i<=t;i++)
    {
        A[i]=B[i];
     } 
}
int main()
{
    int n;
    cin>>n;
    int A[n];
    for(int i=0;i<n;i++)
      cin>>A[i];
    m_sort(A,0,n-1);
    cout<<ans;
    return 0;
}