机器学习系列（三）——目标函数和损失函数

机器学习基础（三）

目录

• 机器学习基础（三）
  • 4. 目标函数
    • 4.1 为什么要使用目标函数
    • 4.2 目标函数的作用原理
    • 4.3 为什么目标函数是负的
    • 4.4 常见的目标函数
      • 4.4.1 二次代价函数（quadratic cost）：
      • 4.4.2 交叉熵代价函数（cross-entropy）：
      • 4.4.3对数似然代价函数（log-likelihood cost）：
  • 5. 损失函数
    • 5.1 什么是损失函数
    • 5.2 常见的损失函数
    • 5.3 逻辑回归为什么使用对数损失函数
    • 5.4 对数损失函数是如何度量损失的

目录

• 机器学习基础（三）
  • 4. 目标函数
    • 4.1 为什么要使用目标函数
    • 4.2 目标函数的作用原理
    • 4.3 为什么目标函数是负的
    • 4.4 常见的目标函数
      • 4.4.1 二次代价函数（quadratic cost）：
      • 4.4.2 交叉熵代价函数（cross-entropy）：
      • 4.4.3对数似然代价函数（log-likelihood cost）：
  • 5. 损失函数
    • 5.1 什么是损失函数
    • 5.2 常见的损失函数
    • 5.3 逻辑回归为什么使用对数损失函数
    • 5.4 对数损失函数是如何度量损失的

目录

• 机器学习基础（三）
  • 4. 目标函数
    • 4.1 为什么要使用目标函数
    • 4.2 目标函数的作用原理
    • 4.3 为什么目标函数是负的
    • 4.4 常见的目标函数
      • 4.4.1 二次代价函数（quadratic cost）：
      • 4.4.2 交叉熵代价函数（cross-entropy）：
      • 4.4.3对数似然代价函数（log-likelihood cost）：
  • 5. 损失函数
    • 5.1 什么是损失函数
    • 5.2 常见的损失函数
    • 5.3 逻辑回归为什么使用对数损失函数
    • 5.4 对数损失函数是如何度量损失的

在本文中着重介绍机器学习中的目标函数（代价函数，Cost Function）以及损失函数（Loss Function），并对涉及到的一些数学概念(最大似然函数、交叉熵、最小二乘法)进行相应的阐述和辨析。

4. 目标函数

4.1 为什么要使用目标函数

1. 为了得到训练逻辑回归模型的参数，需要一个目标函数，通过训练目标函数来得到参数。
2. 用于找到最优解的目的函数。

4.2 目标函数的作用原理

在回归问题中，通过目标函数来求解最优解，常用的是平方误差（最小二乘线性回归）代价函数。假设函数图像如图2-4所示，当参数发生变化时，假设函数状态也会随着变化。

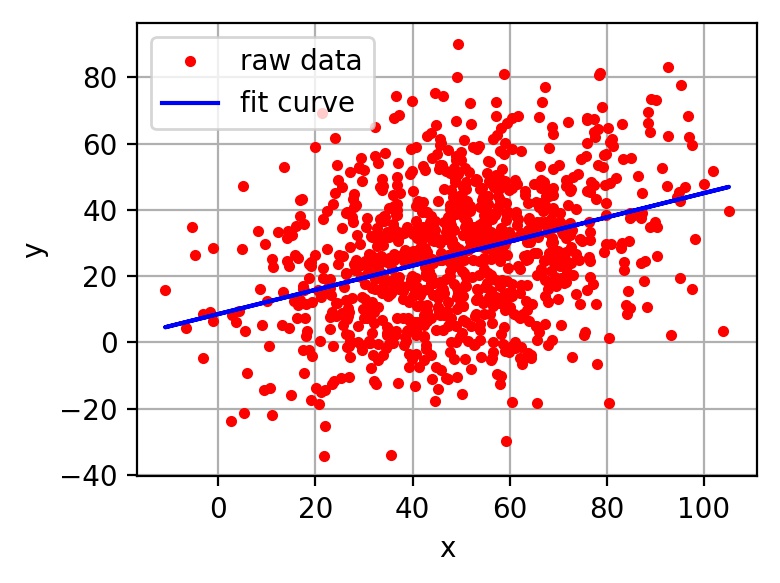
想要拟合图中的离散点，我们需要尽可能找到最优的和来使这条直线更能代表所有数据。如何找到最优解呢，这就需要使用代价函数来求解，以平方误差代价函数为例，假设函数为。 ​ 平方误差代价函数的主要思想就是将实际数据给出的值与拟合出的线的对应值做差，求出拟合出的直线与实际的差距。在实际应用中，为了避免因个别极端数据产生的影响，采用类似方差再取二分之一的方式来减小个别数据的影响。因此，引出代价函数：

\[J(\theta_0, \theta_1) = \frac{1}{m}\sum_{i=1}^m(h(x^{(i)})-y^{(i)})^2 \]

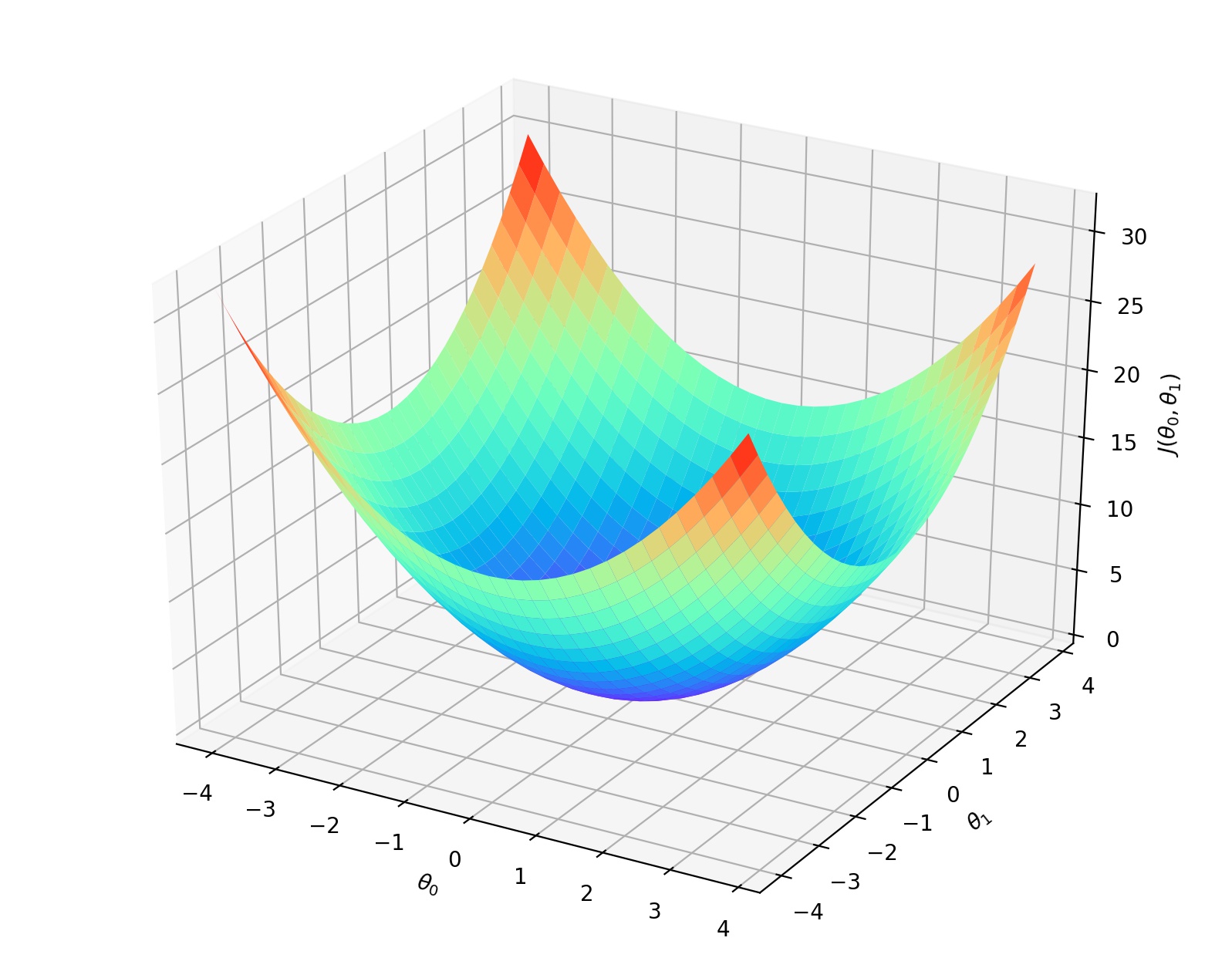
最优解即为代价函数的最小值。如果是1个参数，代价函数一般通过二维曲线便可直观看出。如果是2个参数，代价函数通过三维图像可看出效果，参数越多，越复杂。 当参数为2个时，代价函数是三维图像。

4.3 为什么目标函数是负的

目标函数存在一个下界，在优化过程当中，如果优化算法能够使目标函数不断减小，根据单调有界准则（参见优化方法），这个优化算法就能证明是收敛有效的。 ​ 只要设计的目标函数有下界，基本上都可以，代价函数非负更为方便。

4.4 常见的目标函数

4.4.1 二次代价函数（quadratic cost）：

\[J = \frac{1}{2n}\sum_x\Vert y(x)-a^L(x)\Vert^2 \]

​ 其中，\(J\)表示代价函数，\(x\)表示样本，\(y\)表示实际值，\(a\)表示输出值，\(n\)表示样本的总数。使用一个样本为例简单说明，此时二次代价函数为：

\[J = \frac{(y-a)^2}{2} \]

​ 假如使用梯度下降法（Gradient descent）来调整权值参数的大小，权值\(w\)和偏置\(b\)的梯度推导如下：

\[\frac{\partial J}{\partial b}=(a-y)\sigma'(z) \]

\[\frac{\partial J}{\partial w}=(a-y)\sigma'(z)*x \]

其中，\(z\)表示神经元的输入，\(a=\sigma(z)\)其中\(z=wx+b\)，\(\sigma\)表示激活函数。权值\(w\)和偏置\(b\)的梯度跟激活函数的梯度成正比，激活函数的梯度越大，权值\(w\)和偏置\(b\)的大小调整得越快，训练收敛得就越快。

注：神经网络常用的激活函数为sigmoid函数，该函数的曲线如下图2-6所示：

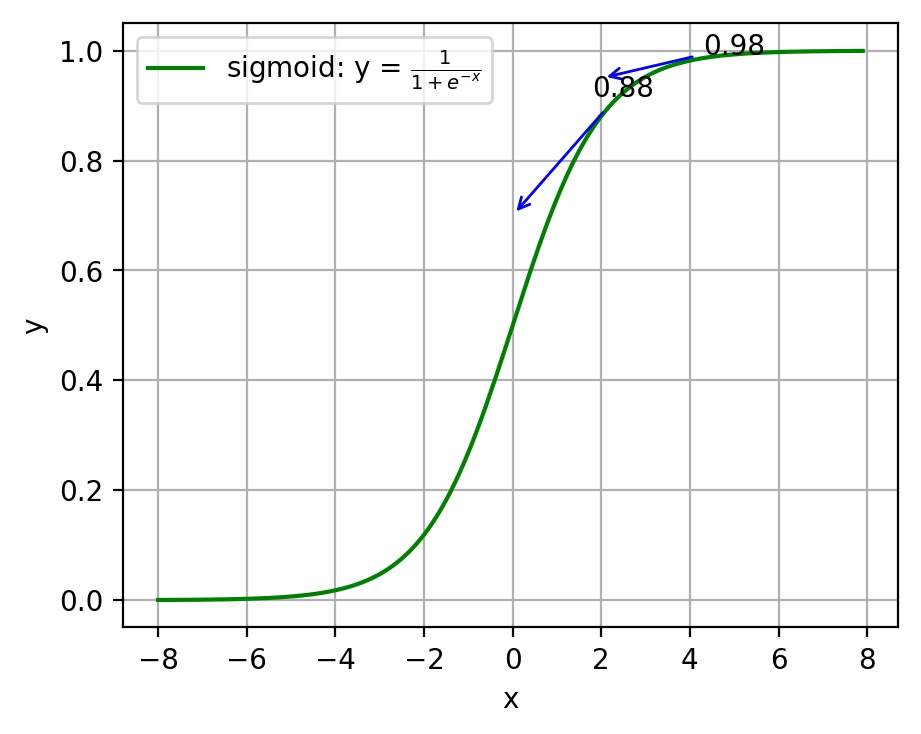
如上图所示，对0.88和0.98两个点进行比较：
​ 假设目标是收敛到1.0。0.88离目标1.0比较远，梯度比较大，权值调整比较大。0.98离目标1.0比较近，梯度比较小，权值调整比较小。调整方案合理。
​ 假如目标是收敛到0。0.88离目标0比较近，梯度比较大，权值调整比较大。0.98离目标0比较远，梯度比较小，权值调整比较小。调整方案不合理。
​ 原因：在使用sigmoid函数的情况下, 初始的代价（误差）越大，导致训练越慢。

4.4.2 交叉熵代价函数（cross-entropy）：

公式的推导：从两个方面考虑
大佬的推导

• 交叉熵的定义
• 对数似然估计

\[J = -\frac{1}{n}\sum_x[y\ln a + (1-y)\ln{(1-a)}] \]

其中，\(J\)表示代价函数，\(x\)表示样本，\(y\)表示实际值，\(a\)表示输出值，\(a=\sigma(z)\)其中\(z=wx+b\)，\(n\)表示样本的总数。
权值\(w\)和偏置\(b\)的梯度推导如下：

最好自己手动推一下 加深对其的理解

用隐函数求导和链式求导法则得出：

推导公式时需要用到Sigmod函数一基本性质：\(/sigma\)函数导数的性质：\(\sigma'(z)=\sigma(z)(1-\sigma(z))\)

\[\frac{\partial J}{\partial w_j}=\frac{1}{n}\sum_{x}x_j(\sigma{(z)}-y)\;， \frac{\partial J}{\partial b}=\frac{1}{n}\sum_{x}(\sigma{(z)}-y) \]

当误差越大时，梯度就越大，权值\(w\)和偏置\(b\)调整就越快，训练的速度也就越快。

​ 这是一个令人兴奋的表达式，优雅而富有深意。让我们注意一下这个式子中最为关键的一项σ(z)−y ，它其实是告诉我们学习的误差越大，你得到的导数值越大，曲线下降的越快，你的学习速度更快，网络收敛的更快。而且损失对于权重系数的偏导数只与误差有关，且激活函数的导数值无

二次代价函数适合输出神经元是线性的情况，交叉熵代价函数适合输出神经元是S型函数的情况。

4.4.3对数似然代价函数（log-likelihood cost）：

对数似然函数常用来作为softmax回归的目标函数。深度学习中普遍的做法是将softmax作为最后一层，此时常用的代价函数是对数似然代价函数。
对数似然代价函数与softmax的组合和交叉熵与sigmoid函数的组合非常相似。对数似然代价函数在二分类时可以化简为交叉熵代价函数的形式。
对于对数似然函数的推导:主要是Softmax函数的导数

在tensorflow中：
与sigmoid搭配使用的交叉熵函数：tf.nn.sigmoid_cross_entropy_with_logits()。
与softmax搭配使用的交叉熵函数：tf.nn.softmax_cross_entropy_with_logits()。
在pytorch中：
与sigmoid搭配使用的交叉熵函数：torch.nn.BCEWithLogitsLoss()。
与softmax搭配使用的交叉熵函数：torch.nn.CrossEntropyLoss()。

为什么用交叉熵代替二次代价函数
（1）为什么不用二次方代价函数
由上一节可知，权值\(w\)和偏置\(b\)的偏导数为\(\frac{\partial J}{\partial w}=(a-y)\sigma'(z)x\)，\(\frac{\partial J}{\partial b}=(a-y)\sigma'(z)\)， 偏导数受激活函数的导数影响，sigmoid函数导数在输出接近0和1时非常小，导数小，差值error也小，会导致一些实例在刚开始训练时学习得非常慢。
（2）为什么要用交叉熵
交叉熵函数权值\(w\)和偏置\(b\)的梯度推导为：

\[\frac{\partial J}{\partial w_j}=\frac{1}{n}\sum_{x}x_j(\sigma{(z)}-y)\;， \frac{\partial J}{\partial b}=\frac{1}{n}\sum_{x}(\sigma{(z)}-y) \]

由以上公式可知，权重学习的速度受到\(\sigma{(z)}-y\)影响，更大的误差，就有更快的学习速度，避免了二次代价函数方程中因\(\sigma'{(z)}\)导致的学习缓慢的情况。

5. 损失函数

5.1 什么是损失函数

​ 损失函数（Loss Function）又叫做误差函数，用来衡量算法的运行情况，估量模型的预测值与真实值的不一致程度，是一个非负实值函数，通常使用\( L(Y, f(x))\)来表示。损失函数越小，模型的鲁棒性就越好。损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。

经验风险函数和结构风险函数的解释，见下面章节代价函数 损失函数和目标函数的区别。

5.2 常见的损失函数

​ 机器学习通过对算法中的目标函数进行不断求解优化，得到最终想要的结果。分类和回归问题中，通常使用损失函数或代价函数作为目标函数。
​损失函数用来评价预测值和真实值不一样的程度。通常损失函数越好，模型的性能也越好。
​ 损失函数可分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是在经验风险损失函数上加上正则项。
​ 下面介绍常用的损失函数：

（1）0-1损失函数
如果预测值和目标值相等，值为0，如果不相等，值为1。

\[L(Y, f(x)) = \begin{cases} 1,& Y\ne f(x)\\ 0,& Y = f(x) \end{cases} \]

一般的在实际使用中，相等的条件过于严格，可适当放宽条件：

\[L(Y, f(x)) = \begin{cases} 1,& |Y-f(x)|\geqslant T\\ 0,& |Y-f(x)|< T \end{cases} \]

（2）绝对值损失函数
和0-1损失函数相似，绝对值损失函数表示为：

\[L(Y, f(x)) = |Y-f(x)|​ \]

（3）平方损失函数

\[L(Y, f(x)) = \sum_N{(Y-f(x))}^2 \]

这点可从最小二乘法和欧几里得距离角度理解。最小二乘法的原理是，最优拟合曲线应该使所有点到回归直线的距离和最小。

（4）对数损失函数

\[L(Y, P(Y|X)) = -\log{P(Y|X)} \]

​ 常见的逻辑回归使用的就是对数损失函数，有很多人认为逻辑回归的损失函数是平方损失，其实不然。逻辑回归它假设样本服从伯努利分布（0-1分布），进而求得满足该分布的似然函数，接着取对数求极值等。逻辑回归推导出的经验风险函数是最小化负的似然函数，从损失函数的角度看，就是对数损失函数。

（6）指数损失函数
指数损失函数的标准形式为：

\[L(Y, f(x)) = \exp(-Yf(x)) \]

例如AdaBoost就是以指数损失函数为损失函数。

（7）Hinge损失函数
Hinge损失函数的标准形式如下：

\[L(y) = \max{(0, 1-ty)} \]

统一的形式：

\[L(Y, f(x)) = \max{(0, Yf(x))} \]

其中y是预测值，范围为(-1,1)，t为目标值，其为-1或1。

在线性支持向量机中，最优化问题可等价于

\[\underset{\min}{w,b}\sum_{i=1}^N (1-y_i(wx_i+b))+\lambda\Vert w\Vert ^2 \]

上式相似于下式

\[\frac{1}{m}\sum_{i=1}^{N}l(wx_i+by_i) + \Vert w\Vert ^2 \]

其中\(l(wx_i+by_i)\)是Hinge损失函数，\(\Vert w\Vert ^2\)可看做为正则化项。

5.3 逻辑回归为什么使用对数损失函数

• 对于似然函数的理解：

  似然则用来描述已知随机变量输出结果时，未知参数的可能取值。似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。对同一个似然函数，如果存在一个参数值，使得它的函数值达到最大的话，那么这个值就是最为“合理”的参数值。
  最大似然函数： 是指找出一个（θ）的组合，使得\(L（θ）=L（x1,x2,…,xn；θ）=ΠP（xi；θ\)最大化，即使得样本数据出现的概率最大化
  似然函数取得最大值表示相应的参数能够使得统计模型最为合理
  从这样一个想法出发，最大似然估计的做法是：

• 首先选取似然函数（一般是 概率密度函数或概率质量函数），

• 整理之后求最大值。实际应用中一般会取似然函数的对数作为求最大值的函数，这样求出的最大值和直接求最大值得到的结果是相同的。

  统计学的观点始终是认为样本的出现是基于一个分布的。那么我们去假设这个分布为f，里面有参数theta。对于不同的theta，样本的分布不一样。f(x|θ)表示的就是在给定参数theta的情况下，x出现的可能性多大。L(θ|x)表示的是在给定样本x的时候，哪个参数theta使得x出现的可能性多大。

假设逻辑回归模型

\[P(y=1|x;\theta)=\frac{1}{1+e^{-\theta^{T}x}} \]

假设逻辑回归模型的概率分布是伯努利分布0-1两点分布，其概率质量函数为：

\[P(X=n)= \begin{cases} 1-p, n=0\\ p,n=1 \end{cases} \]

其似然函数为：

\[L(\theta)=\prod_{i=1}^{m} P(y=1|x_i)^{y_i}P(y=0|x_i)^{1-y_i} \]

对数似然函数为：

\[\ln L(\theta)=\sum_{i=1}^{m}[y_i\ln{P(y=1|x_i)}+(1-y_i)\ln{P(y=0|x_i)}]\\ =\sum_{i=1}^m[y_i\ln{P(y=1|x_i)}+(1-y_i)\ln(1-P(y=1|x_i))] \]

对数函数在单个数据点上的定义为：

\[cost(y,p(y|x))=-y\ln{p(y|x)-(1-y)\ln(1-p(y|x))} \]

则全局样本损失函数为：

\[cost(y,p(y|x)) = -\sum_{i=1}^m[y_i\ln p(y_i|x_i)+(1-y_i)\ln(1-p(y_i|x_i))] \]

由此可看出，对数损失函数与极大似然估计的对数似然函数本质上是相同的。所以逻辑回归直接采用对数损失函数。

5.4 对数损失函数是如何度量损失的

​ 例如，在高斯分布中，我们需要确定均值和标准差。
​ 如何确定这两个参数？最大似然估计是比较常用的方法。最大似然的目标是找到一些参数值，这些参数值对应的分布可以最大化观测到数据的概率。
​ 因为需要计算观测到所有数据的全概率，即所有观测到的数据点的联合概率。现考虑如下简化情况：

（1）假设观测到每个数据点的概率和其他数据点的概率是独立的。

（2）取自然对数。
假设观测到单个数据点\(x_i(i=1,2,...n)\)的概率为：（正态分布）

\[P(x_i;\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}\exp \left( - \frac{(x_i-\mu)^2}{2\sigma^2} \right) \]

（3）其联合概率为：连乘取似然函数

\[P(x_1,x_2,...,x_n;\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}\exp \left( - \frac{(x_1-\mu)^2}{2\sigma^2} \right) \\ \times \frac{1}{\sigma \sqrt{2\pi}}\exp \left( - \frac{(x_2-\mu)^2}{2\sigma^2} \right) \times ... \times \frac{1}{\sigma \sqrt{2\pi}}\exp \left( - \frac{(x_n-\mu)^2}{2\sigma^2} \right) \]

​ 对上式取自然对数，可得：

\[ \ln(P(x_1,x_2,...x_n;\mu,\sigma))= \ln \left(\frac{1}{\sigma \sqrt{2\pi}} \right) - \frac{(x_1-\mu)^2}{2\sigma^2} \\ + \ln \left( \frac{1}{\sigma \sqrt{2\pi}} \right) - \frac{(x_2-\mu)^2}{2\sigma^2} +...+ \ln \left( \frac{1}{\sigma \sqrt{2\pi}} \right) - \frac{(x_n-\mu)^2}{2\sigma^2} \]

根据对数定律，上式可以化简为：

\[\ln(P(x_1,x_2,...x_n;\mu,\sigma))=-n\ln(\sigma)-\frac{n}{2} \ln(2\pi)\\ -\frac{1}{2\sigma^2}[(x_1-\mu)^2+(x_2-\mu)^2+...+(x_n-\mu)^2] \]

然后求导为：

\[\frac{\partial\ln(P(x_1,x_2,...,x_n;\mu,\sigma))}{\partial\mu}= \frac{n}{\sigma^2}[\mu - (x_1+x_2+...+x_n)] \]

​ 上式左半部分为对数损失函数。损失函数越小越好，因此我们令等式左半的对数损失函数为0，可得：

\[\mu=\frac{x_1+x_2+...+x_n}{n} \]

同理，可计算\(\sigma\)。