线性回归-梯度下降

上了篇尝试了利用穷举法来求较好的模型，但是穷举法的效率很低。还有一种更高效的方法，梯度下降法（Gradient Descent）。

算法过程

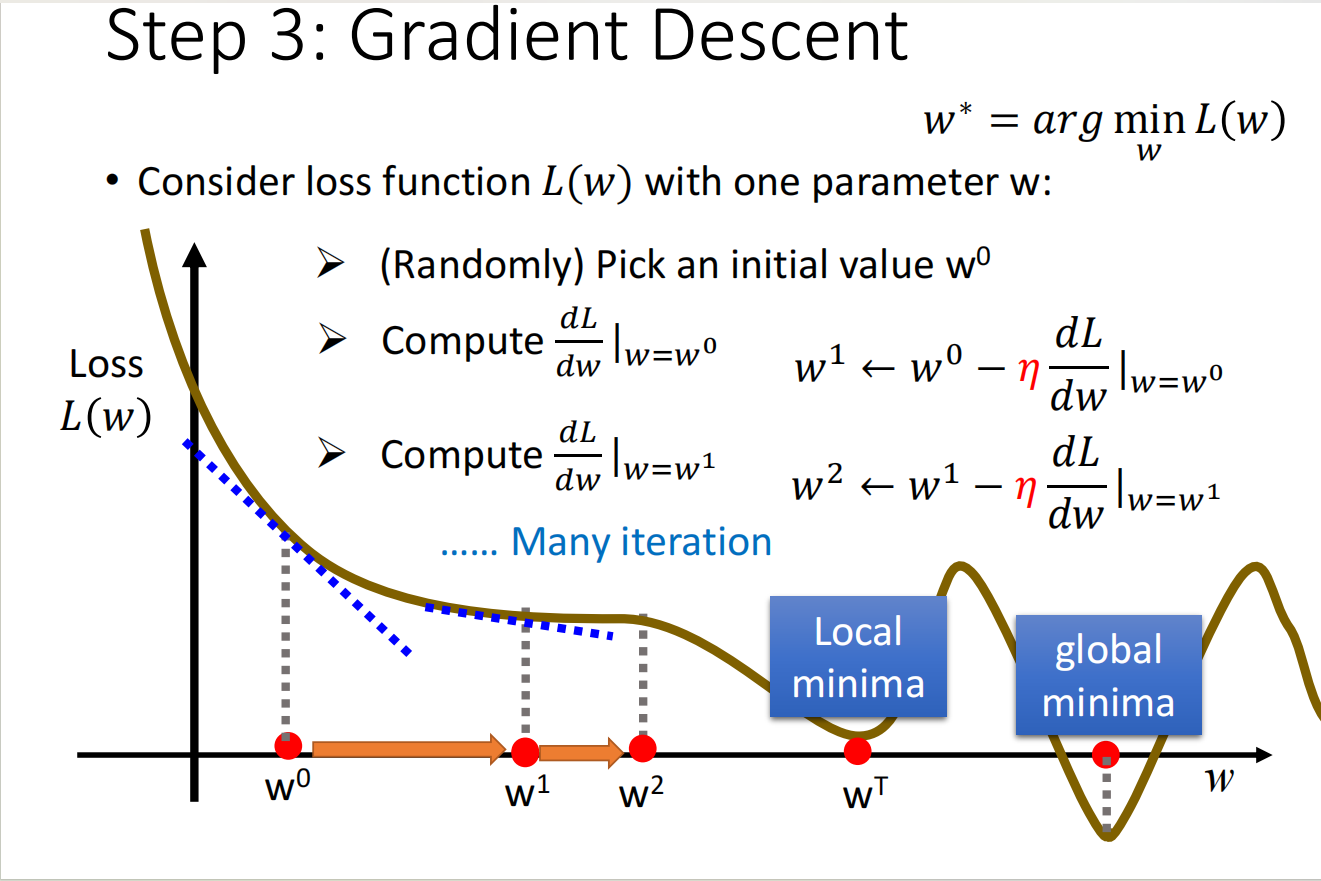
代码实现

x = [338., 333., 328., 207., 226., 25., 179., 70., 208., 606.]
y = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]
w, b = 0, 0
l = 0.000001
iteration = 1000000
for i in range(iteration):
    w_grad, b_grad = 0.0, 0.0
    for n in range(len(x)):
        w_grad = w_grad - 2 * (y[n] - (w * x[n] + b)) * x[n]
        b_grad = b_grad - 2 * (y[n] - (w * x[n] + b))
    w = w - l * w_grad
    b = b - l * b_grad
    print(w, b)

输出：

点击查看结果

973658 -16.385095312542127
2.1727336549395617 -16.386086173869376
2.172736509566115 -16.387077029766793
2.172739364177025 -16.38806788023441
2.172742218772292 -16.389058725272257
2.172745073351916 -16.390049564880364
2.1727479279158977 -16.39104039905876
2.172750782464236 -16.392031227807475
………………
2.6912891954252833 -196.37944287569678
2.691289208414678 -196.3794473843842
2.691289221404002 -196.37945189304693
2.6912892343932553 -196.37945640168496
2.6912892473824366 -196.37946091029826
2.6912892603715473 -196.37946541888687
2.6912892733605864 -196.37946992745077
2.6912892863495546 -196.37947443598995
2.6912892993384516 -196.37947894450443
2.6912893123272768 -196.3794834529942
2.691289325316032 -196.3794879614593
2.691289338304715 -196.37949246989965
2.6912893512933276 -196.3794969783153
2.6912893642818685 -196.37950148670626
2.691289377270339 -196.37950599507252
2.691289390258737 -196.37951050341405
2.6912894032470653 -196.3795150117309
2.6912894162353207 -196.37951952002302
2.691289429223507 -196.37952402829046
2.6912894422116205 -196.37952853653317
2.691289455199663 -196.37953304475118
2.691289468187635 -196.3795375529445
2.6912894811755357 -196.3795420611131
2.6912894941633647 -196.379546569257
2.691289507151123 -196.3795510773762
2.69128952013881 -196.37955558547068
2.6912895331264255 -196.37956009354048
2.6912895461139703 -196.37956460158557
2.691289559101444 -196.37956910960597
2.6912895720888463 -196.37957361760164
2.6912895850761775 -196.3795781255726
2.6912895980634373 -196.37958263351888
2.6912896110506264 -196.37958714144045
2.6912896240377435 -196.37959164933733
2.6912896370247905 -196.3795961572095
2.6912896500117656 -196.37960066505696
2.6912896629986696 -196.3796051728797
2.6912896759855025 -196.37960968067776
2.6912896889722644 -196.37961418845111
2.6912897019589552 -196.37961869619977
2.6912897149455746 -196.37962320392373
2.691289727932123 -196.379627711623
2.6912897409186 -196.37963221929752
2.691289753905006 -196.37963672694735
2.691289766891341 -196.3796412345725
2.691289779877604 -196.37964574217293
2.6912897928637967 -196.37965024974866
2.691289805849918 -196.3796547572997
2.691289818835968 -196.37965926482605
2.6912898318219476 -196.3796637723277
2.6912898448078546 -196.37966827980463
2.6912898577936923 -196.37967278725688
2.691289870779457 -196.37967729468443
2.691289883765152 -196.37968180208725
2.6912898967507743 -196.37968630946537
2.691289909736327 -196.3796908168188
2.6912899227218072 -196.37969532414752
2.6912899357072173 -196.37969983145155
2.6912899486925554 -196.37970433873087
2.6912899616778234 -196.3797088459855
2.691289974663019 -196.37971335321544
2.691289987648145 -196.37971786042067
2.691290000633198 -196.3797223676012
2.6912900136181817 -196.37972687475704
2.691290026603092 -196.37973138188818
2.6912900395879333 -196.37973588899462
2.691290052572702 -196.37974039607636
2.691290065557401 -196.3797449031334
2.691290078542027 -196.37974941016574
2.6912900915265836 -196.3797539171734
2.6912901045110678 -196.37975842415634
2.6912901174954817 -196.37976293111458
2.6912901304798234 -196.37976743804813
2.6912901434640952 -196.37977194495699
2.6912901564482947 -196.37977645184114
2.691290169432424 -196.3797809587006
2.6912901824164814 -196.37978546553535
2.691290195400468 -196.3797899723454
2.6912902083843835 -196.37979447913077
2.6912902213682277 -196.37979898589143
2.6912902343520013 -196.37980349262742
2.6912902473357025 -196.3798079993387
2.691290260319334 -196.3798125060253
2.6912902733028936 -196.3798170126872
2.691290286286382 -196.3798215193244
2.6912902992698 -196.3798260259369
2.6912903122531455 -196.3798305325247
2.6912903252364213 -196.3798350390878
2.6912903382196243 -196.3798395456262
2.691290351202758 -196.3798440521399
2.6912903641858192 -196.3798485586289
2.69129037716881 -196.37985306509324
2.691290390151729 -196.37985757153288
2.6912904031345777 -196.37986207794782
2.6912904161173543 -196.37986658433806
2.6912904291000608 -196.3798710907036
2.691290442082695 -196.37987559704445
2.691290455065259 -196.3798801033606
2.691290468047751 -196.37988460965207
2.691290481030173 -196.37988911591884
2.691290494012523 -196.37989362216092
2.691290506994802 -196.3798981283783
2.69129051997701 -196.37990263457098
2.6912905329591466 -196.37990714073896
2.6912905459412126 -196.37991164688228
2.691290558923207 -196.3799161530009
2.6912905719051308 -196.3799206590948

重难点

对上面的公式求偏导得：