线性回归-穷举法

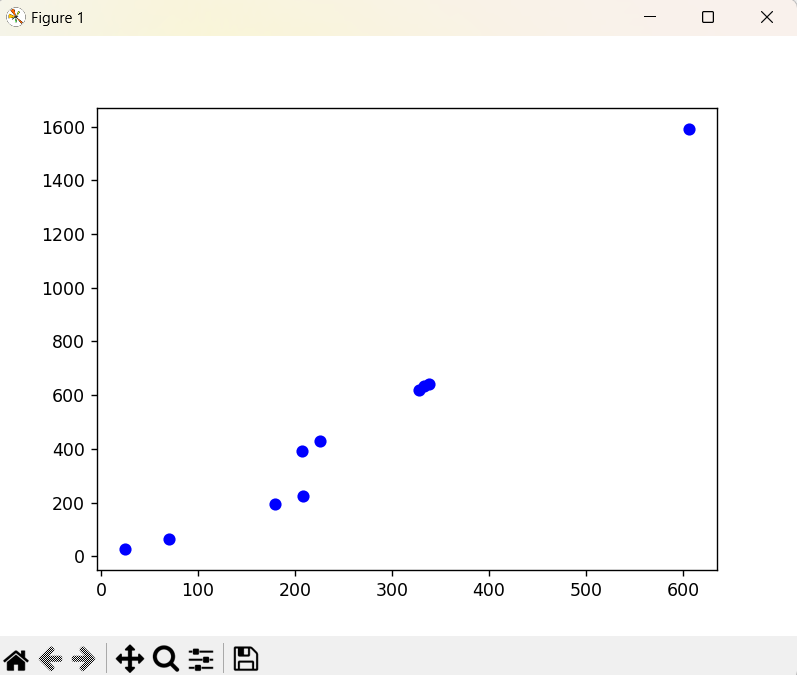
样本：有十个点

假设有十个点，用matplotlib画出来

import matplotlib.pyplot as plt

cp = [338., 333., 328., 207., 226., 25., 179., 70., 208., 606.]
y = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]
plt.plot(cp, y, 'bo')
plt.show()

如下图所示：

模型

y=wx+b

定义损失函数

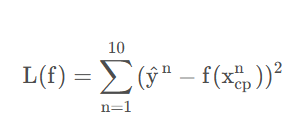
因为f是由w,b决定的，因此上面的损失函数可以转换为

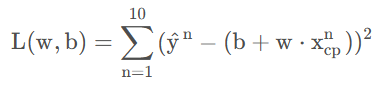
穷举法找到w,b

import matplotlib.pyplot as plt
import numpy as np
x = [338., 333., 328., 207., 226., 25., 179., 70., 208., 606.]
y = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]

x_data=np.arange(-200,-100,1)
y_data=np.arange(-5,5,0.1)

minb,minw,min_loss=0,0, 10 ** 5
for i in range(len(x_data)):
    for j in range(len(y_data)):
        b,w=x_data[i],y_data[j]
        temp_loss=0
        for k in range(len(x)):
            temp_loss+=(y[k]-(w*x[k]+b))**2
        if temp_loss<min_loss:
            min_loss=temp_loss
            minb,minw=x_data[i],y_data[j]
print(minb,minw,min_loss)

控制台输出是

-199 2.6999999999999726 97414.91999999995

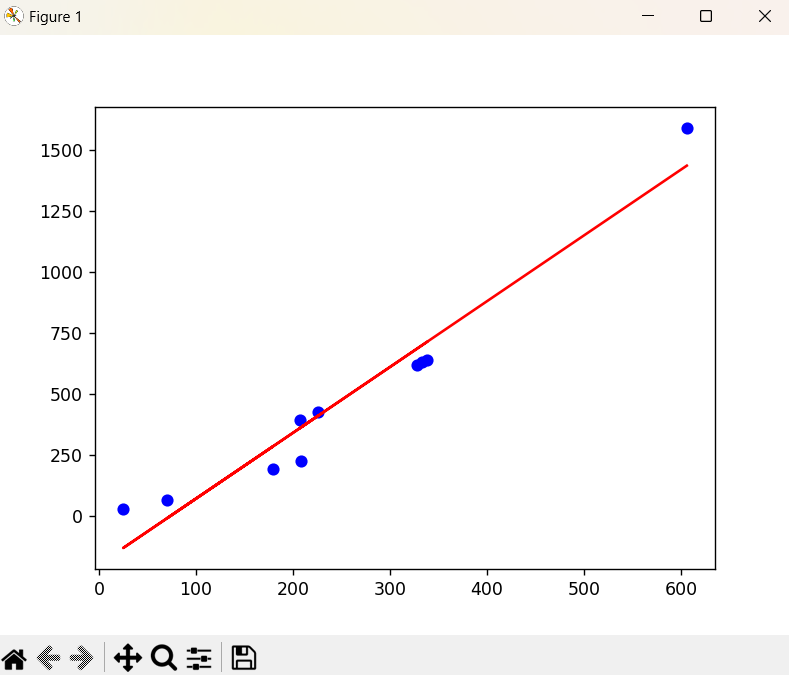
在图上拟合

import matplotlib.pyplot as plt
import numpy as np
cp = [338., 333., 328., 207., 226., 25., 179., 70., 208., 606.]
y = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]
y_head =  -199 + 2.699 * np.array(cp)
plt.plot(cp, y, 'bo')
plt.plot(cp, y_head, 'r-')
plt.show()

画出的图如下：