结对项目
| 这个作业属于哪个课程 | 19网工3、4班 |
|---|---|
| 作业要求 | 结对项目 |
| 作业目标 | 一个自动生成小学四则运算题目的程序 |
| 队员 | 3219005405杨芳 3219005406周凤秀 |
github
1、PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 1020 | 1160 |
| Development | 开发 | 880 | 1060 |
| · Analysis | · 需求分析 (包括学习新技术) | 200 | 320 |
| · Design Spec | · 生成设计文档 | 80 | 60 |
| · Design Review | · 设计复审 | 30 | 30 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 30 |
| · Design | · 具体设计 | 100 | 80 |
| · Coding | · 具体编码 | 240 | 300 |
| · Code Review | · 代码复审 | 60 | 60 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 60 |
| Reporting | 报告 | 60 | 90 |
| · Test Repor | · 测试报告 | 20 | 30 |
| · Size Measurement | · 计算工作量 | 50 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 60 | 40 |
| 合计 | 1020 | 1160 |
2、计算模块接口的性能与实现过程
(1)项目结构
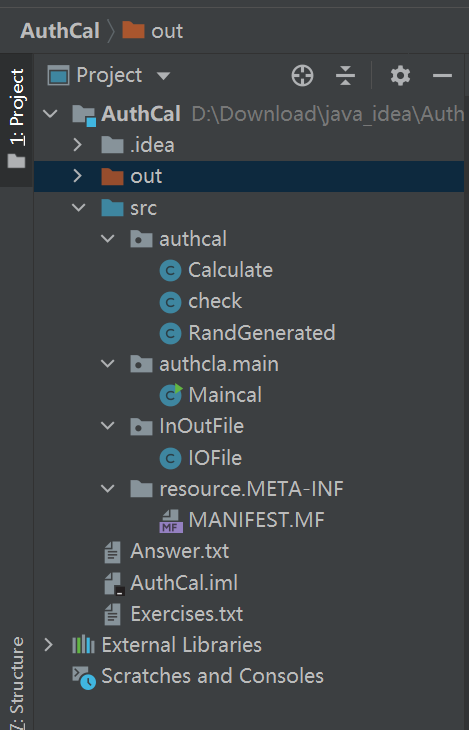
(2)程序实现类
- 主类
Maincal:传入参数,控制生成题目的数量以及控制题目中数字的范围。 - 文件读写类
IOFile:创建文件,通过调用式子生成类生成需要的题目,并将题目及答案分别写进文件中 - 式子生成类
RandGenerated:随机生成数学表达式,数字包括整数、分数,当出现e1-e2的形式时,e1>e2,出现e1/e2时,结果会化为最简分数或者带分数 - 查重类
Check:判断有没有两条相同的式子,如果经过有限次交换可得到相同的式子,则重新生成 - 计算类
Calculate:通过逆波兰表达式将中缀表达式化为后缀表达式,从而得到数学表达式的结果
(3)项目流程
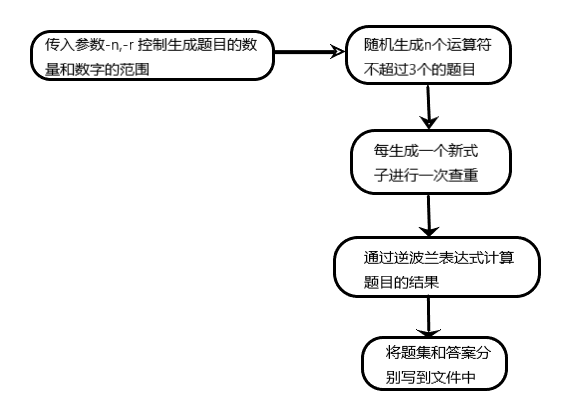
关键函数的实现与分析
实现四则运算的一个关键部分是计算表达式的结果,这里通过逆波兰表达式将中缀表达式转化成后缀表达式来实现。
参考: 详解逆波兰式与表达式求值
对于计算一个算式 如 : 3*(5+6)-2
这种算式叫做中缀表达式, 人们看着会比较方便, 如果用计算机直接计算会很麻烦,所以要把中缀表达式变为计算机易于理解的后缀表达式来计算,后缀表达式又叫逆波兰表达式, 把运算量写在前面, 把运算符写在后面, 并且可以去掉括号。
如 a+b 变为 a b +
a*(b+c) 可以变为 a b c + *
将普通算式转化为逆波兰表达式的步骤如下:
-
从左到右扫描算式, 如果是数字, 计算数字的值后直接输出。
-
如果是左括号, 直接加入栈。
-
如果是右括号,查询栈顶是否为左括号, 如果是, 把左括号出栈,如果不是,输出栈顶的符号, 出栈, 继续第三步, 直到找到左括号。
-
如果是 +, -, *, /, 运算符,比较当前运算符和栈顶运算符的优先级,如果该运算符的优先级大于栈顶运算符的优先级或者栈为空或者栈顶符号为括号, 把该运算符入栈,否则, 也就是小于等于的情况, 输出栈顶的符号, 出栈。
在代码实现的过程中,我们对逆波兰表达式进行了一个变换,即采用String数组来存储: 操作数1 操作数2 操作符 计算结果 这样的一个形式,而不是原始的逆波兰表达式的:操作数 操作数 操作符 操作数/操作符....这样的形式,这样方便于最后的计算结果
在将表达式入栈的过程中,还使用到了hashmap来存储运算符的优先级,用于比较栈顶元素及当前运算符的优先级。
部分代码展示
public class Calculate {
/**
* 检查式子结果、生成逆波兰表达式
* @param formula 为 式子
* @return reversePolishNotation 为 当前式子 的 (改良)后缀表达式 && 结果 && 字符串形式 的 数组
*/
public String[] checkout(String formula,int length){
Stack<String> stackNumber = new Stack<>(); //操作数
Stack<String> stackOperator = new Stack<>(); //操作符
String[] reversePolishNotation = new String[length];//逆波兰表达式
// 哈希表 存放运算符优先级
HashMap<String, Integer> hashmap = new HashMap<>();
hashmap.put("(", 0);
hashmap.put("+", 1);
hashmap.put("-", 1);
hashmap.put("×", 2);
hashmap.put("÷", 2);
for (int i=0,j=0; i < formula.length();) {
StringBuilder digit = new StringBuilder();
char c = formula.charAt(i);
while (Character.isDigit(c)||c=='/'||c=='\'') {
digit.append(c);
i++;
c = formula.charAt(i);
}
if (digit.length() == 0){
switch (c) {
case '(': {
stackOperator.push(String.valueOf(c));
break;
}
case ')': {
//将 stackOperator 栈顶元素取到 operator
String operator = stackOperator.pop();
//当前符号栈里面还有 + - × ÷时,取 操作数 并 运算
while (!stackOperator.isEmpty() && !operator.equals("(")) {
//取操作数a,b
String a = stackNumber.pop();
String b = stackNumber.pop();
//后缀表达式变形
reversePolishNotation[j++] = a;
reversePolishNotation[j++] = b;
reversePolishNotation[j++] = operator;
String ansString = calculate(b, a, operator);
if(ansString == null)
return null;
//将结果压入栈
stackNumber.push(ansString);
//符号指向下一个计算符号
operator = stackOperator.pop();
}
break;
}
case '=': {
String operator;
//当前符号栈里面还有 + - × ÷时,即还没有算完,取 操作数 并 运算
while (!stackOperator.isEmpty()) {
operator = stackOperator.pop();
String a = stackNumber.pop();
String b = stackNumber.pop();
reversePolishNotation[j++] = a;
reversePolishNotation[j++] = b;
reversePolishNotation[j++] = operator;
String ansString = calculate(b, a, operator);
if(ansString == null)
return null;
stackNumber.push(ansString);
}
break;
}
default: {
String operator;
while (!stackOperator.isEmpty()) {
operator = stackOperator.pop();
if (hashmap.get(operator) >= hashmap.get(String.valueOf(c))) { //比较优先级
String a = stackNumber.pop();
String b = stackNumber.pop();
reversePolishNotation[j++] = a;
reversePolishNotation[j++] = b;
reversePolishNotation[j++] = operator;
String ansString =calculate(b, a, operator);
if(ansString == null)
return null;
stackNumber.push(ansString);
}
else {
stackOperator.push(operator);
break;
}
}
stackOperator.push(String.valueOf(c)); //将符号压入符号栈
break;
}
}
}
//处理数字,直接压栈
else {
stackNumber.push(digit.toString());
continue; //结束本次循环,回到for语句进行下一次循环,即不执行i++(因为此时i已经指向符号了)
}
i++;
}
//获取 栈顶数字 即 等式的最终答案
reversePolishNotation[length-3] = "=";
reversePolishNotation[length-2] = stackNumber.peek();
reversePolishNotation[length-1] = formula;
return reversePolishNotation;
}
}
3、模块接口性能部分的性能改进
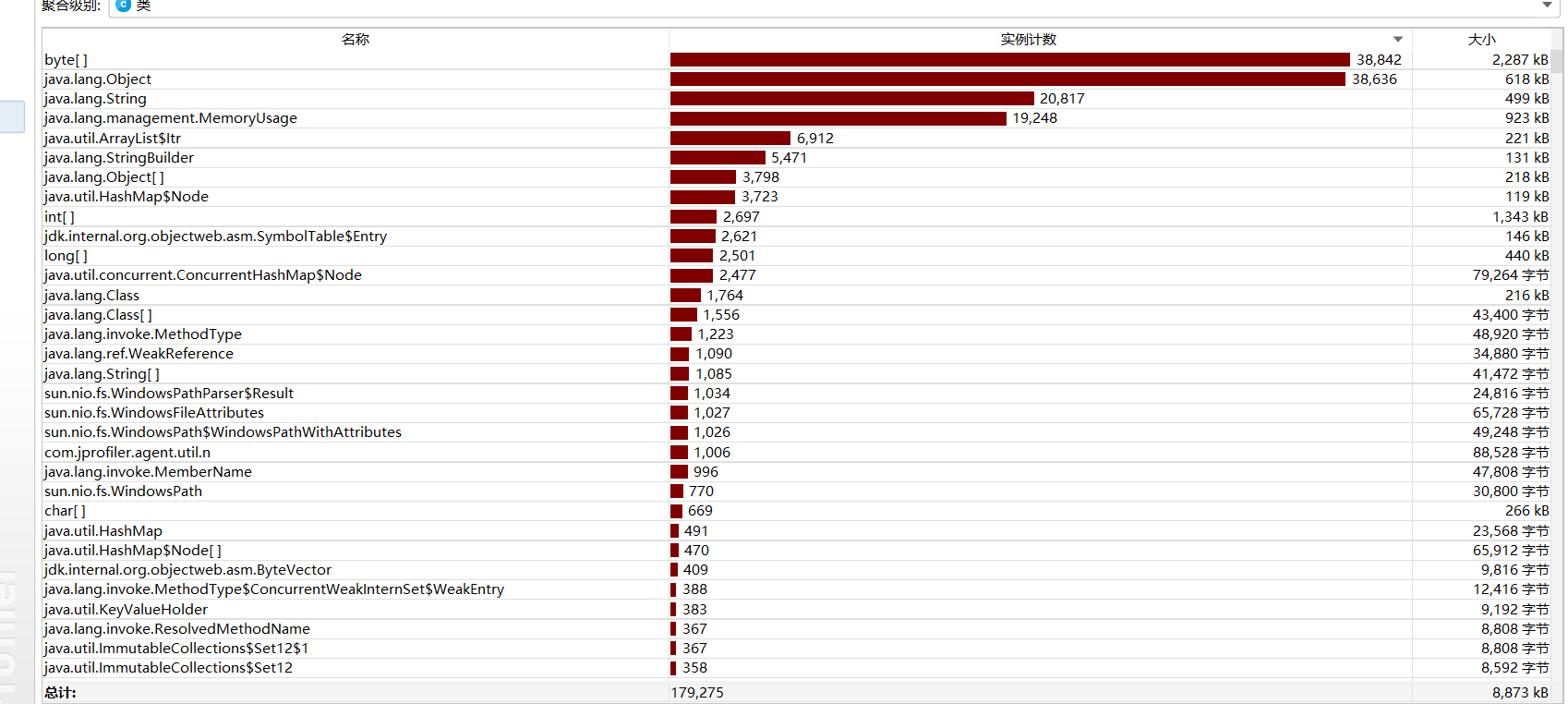
可以看出,最主要的消耗还是文件读写类,选择逆波兰表达式可以有效改善性能问题
3、运行结果
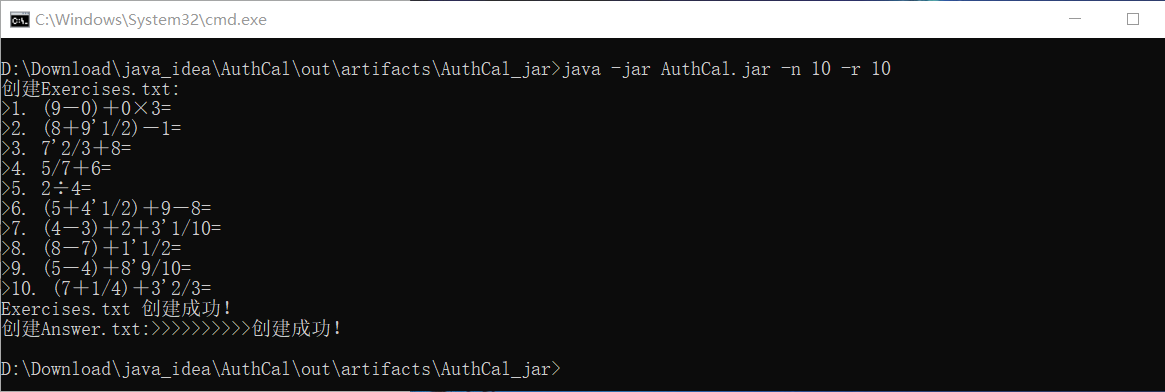


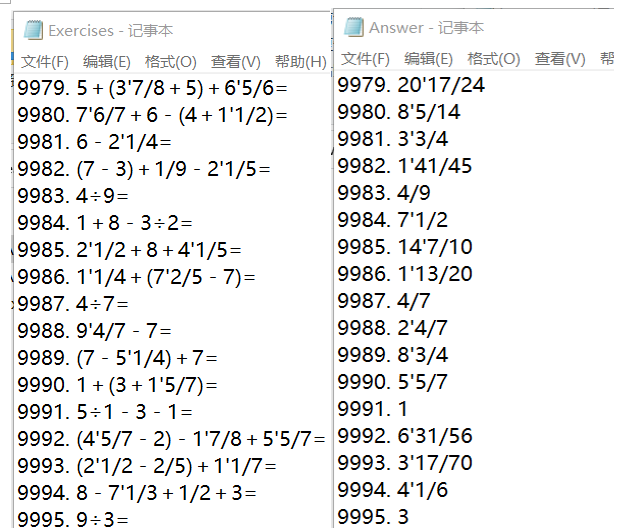
3.项目总结
周凤秀:这是第一次尝试跟别人合作写项目,在交流的过程中,能感觉到自己思路的局限性,因为不同的人对于同一个问题的切入点 不一样,解决思路也不一样,所以写代码的时候多交流还是很有帮助的。
杨芳:通过这次结对项目,我发现两个人一起完成项目比一个人独自干要有趣且更快更高效,而且自己无法发现的问题和漏洞,队友可以给你指出来。我们先互相理出一个思路,再分工完成编程,总的来说,相互沟通的比较好。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号