NLP面试常见的知识点

为什么归一化？

1 处理不同量纲的数据，将其缩放到相同的数据区间和范围。
2 加快计算素的，提高计算精度

归一化的方法？

1 极差变换法（最大最小值变换）

\[y_{i} = \frac{x_{i}-min(x)}{max(x)-min(x)} \]

缺点：归一化过程中容易受到极端值的影响

2 0均值归一化

\[y_{i} = \frac{x_{i}-mean(x)}{\sigma(x)} \]

哪些算法模型需要归一化，哪些不需要归一化？

一般来说，树结构的算法不需要归一化，而寻找最-优解问题的算法则需要数据归一化。
不需要

• 决策树（数值缩放不影响分裂点的位置，对树结构不造成影响）
• 随机森林（树与树之间是独立的，不需要归一化）
• XGbboost
• 朴素贝叶斯：不关系具体取值，只关心分布

需要：

• 线性回归、逻辑回归、SVM
• KNN、K-means
• Adaboost 和 GBDT （GBDT是在上一颗树的基础上通过梯度下降求最优化，归一化收敛更快）

什么样的模型对缺失值敏感？

1 树模型对缺失值的敏感度低，大部分可以在数据缺失的情况中使用
2 涉及到距离变量（如计算两个点之间的距离）如KNN和SVM，缺失数据就变得比较重要，因为涉及到距离，缺失值处理不当就会导致效果很差。
3 线性模型的损失函数往往涉及距离计算，计算预测值与真实值的差别，容易对缺失值敏感。
4 神经网络的鲁棒性强，对缺失数据不敏感
5 贝叶斯模型对于缺失数据也比较稳定。

欠拟合和过拟合的原因及解决方案 ？

• 欠拟合出现的原因：
  1 模型复杂度过低
  2 特征量太少

• 解决办法：
  1 增加新特征
  2 减少正则化参数
  3 模型复杂化（例如在回归模型中增加高次项，神经网络中增加模型层数和隐藏层单元数）

• 过拟合出现的原因：
  1 样本选择有误（样本太少，标签错误等）选择的样本不足以代表整个整个规则
  2 样本噪音过大
  3 参数太多，模型复杂度高

• 解决方法：
  1 正则化
  2 数据扩充（获取更多的数据或者通过一定的规则产生新的数据）
  3 Dropout
  4 Early Stop

类别不平衡问题怎么解决？

什么是类别不平衡问题：值分类任务中，不同类别的训练样例数目差别很大的情况
解决类别不平衡问题的方法：
1 欠采样：对多数类样本进行欠采样
2 过采样：对少数类样本过采样
3 扩大数据集
4 阈值移动：基于原始数据集进行学习，在预测时，将缩放的公式嵌入到决策过程中
5 惩罚算法：增加少数类分错的成本

欠采样：
优：减少样本数据量，改善了运行时间和存储
缺：1 可能丢掉有用的信息，2 通过随机欠采样的样本可能是有偏差的样本

过采样：
优：不会有信息丢失
缺：复制了少数类样本，增加了过拟合的可能性

为什么不用one-hot向量？

1 one-hot向量无法表达不同词之间的相似度，任何一对one-hot向量的余弦距离为零。
2 随着词典的增大，其向量维度也会一直不断变大。
word2vec可以较好的表达出不同此之间的相似和类比关系

word2vec的结构

CBOW模型的计算流程

skip-gram也类似

word2vec的两种训练技巧

两个问题导致word2vec计算量大
（1）词表维度大
（2）softmax计算量大
第一个解决方法：层次softmax
把N个多分类问题变成logn个二分类问题，可以将softmax转换成sigmoid函数，并且还可以利用\(\sigma(x)^{'} = \sigma(x)*(1-\sigma(x))\)
第二个解决方法 高频词抽样+负采样
1 将常见的单词组合或者词组作为单个“word”来处理
2 对高频词单词进行抽样来减少训练样本个数
3 对优化目标采用“negative sampling”方法，这样每个训练样本的训练只会更新一小部分的模型权重，从而降低计算负担

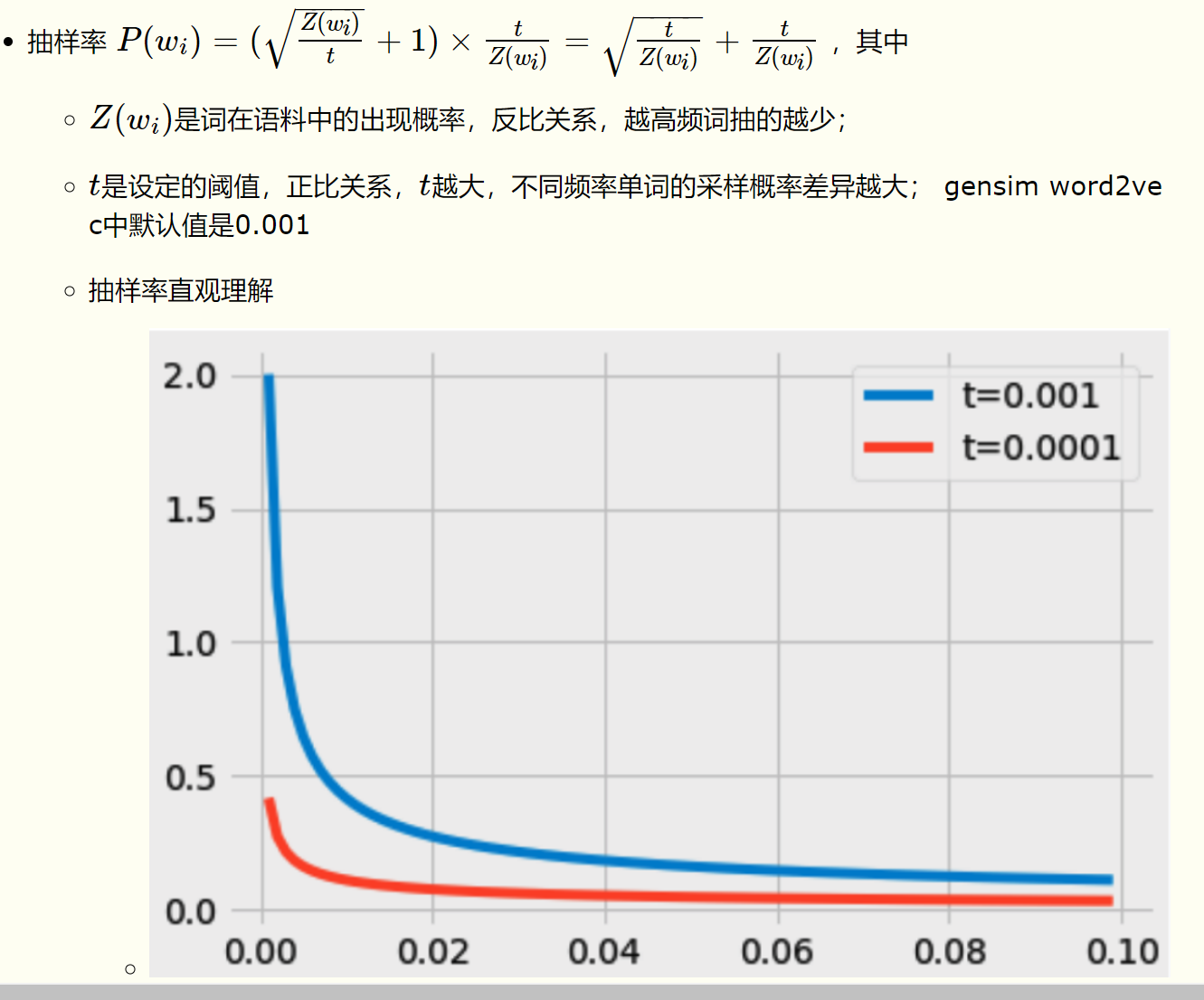
• 高频词抽样
  主要思想是少训练没有区分度的高频term；对于我们在训练原始文本中遇到的每一个单词，它们都有一定概率被我们从文本中删掉，而这个被删除的概率与单词的频率有关。词频越高（stopword），抽样越少；
  
• 负采样
  

常见的损失函数及其优缺点

• sigmoid

\[f(x) = \frac{1}{1+exp(-x)} \]

特点:能够将输入的连续值变换为0和1 之间的输出
缺点：
1 容易梯度消失（因为导数的最大值为0.25，即经过一次sigmoid之后梯度就减少4分之3，当层数很多时，梯度就容易变为0）
补充： 解决梯度消失和梯度爆炸的方法 （梯度爆炸：梯度截断，添加正则化--如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生；梯度消失：改激活函数，batchnorm，残差结构，将RNN换成LSTM）
2 解析式含有幂运算，比较耗时
3 输出数据不是零均值

• tanh

\[tanh(x) = \frac{exp(x)-exp(-x)}{exp(x)+exp(-x)} \]

特点：和sigmoid差不多，值域为【-1，1】，解决了sigmoid不是零均值的问题
缺点：梯度消失和幂运算的问题仍然存在
\(tanh(x/2) = 2*\sigmoid(x) - 1\)

• relu

\[relu(x) = max(0,x) \]

优点：
解决了梯度消失问题
计算速度快，只需要判断输入是否为0
收敛速度远快于sigmoid和tanh
缺点：
输出不是0均值
容易出现神经元坏死，即参数永远无法更新（可能产生这种现象的两个原因:1参数初始化 2 学习率太大）
原点不可导（随意选择一个导数进行替代，默认为0）

• leaky relu

\[f(x) = max(\alpha * x,x) \alpha = 0.01 \]

缓解了relu中神经元坏死的现象

• Elu

\[f(x) =\left\{ \begin{matrix} x ,x>0 \\ \alpha*(exp(x) - 1) \end{matrix} \right. \]

优
不会出现relu中的神经元坏死现象
输出的数值是零均值的
缺：
含有幂运算，计算量稍大

• gelu

\[f(x) = 0.5x(1+tanh([\sqrt{\frac{2}{\pi}}(x+0.044715x^3)]) \]

bert和transformer中使用的激活函数（高斯误差线性单元）

深度学习中batch size的大小对训练过程的影响是什么样的？

不考虑bn的情况下，batch size的大小决定了深度学习训练过程中的完成每个epoch所需的时间和每次迭代(iteration)之间梯度的平滑程度。batch size只能说影响完成每个epoch所需要的时间，决定也算不上吧。根本原因还是CPU，GPU算力吧。瓶颈如果在CPU，例如随机数据增强，batch size越大有时候计算的越慢。

对于一个大小为N的训练集，如果每个epoch中mini-batch的采样方法采用最常规的N个样本每个都采样一次，设mini-batch大小为b，那么每个epoch所需的迭代次数(正向+反向)为 , 因此完成每个epoch所需的时间大致也随着迭代次数的增加而增加。

由于目前主流深度学习框架处理mini-batch的反向传播时，默认都是先将每个mini-batch中每个instance得到的loss平均化之后再反求梯度，也就是说每次反向传播的梯度是对mini-batch中每个instance的梯度平均之后的结果，所以b的大小决定了相邻迭代之间的梯度平滑程度，b太小，相邻mini-batch间的差异相对过大，那么相邻两次迭代的梯度震荡情况会比较严重，不利于收敛；b越大，相邻mini-batch间的差异相对越小，虽然梯度震荡情况会比较小，一定程度上利于模型收敛，但如果b极端大，相邻mini-batch间的差异过小，相邻两个mini-batch的梯度没有区别了，整个训练过程就是沿着一个方向蹭蹭蹭往下走，很容易陷入到局部最小值出不来。

总结下来：batch size过小，花费时间多，同时梯度震荡严重，不利于收敛；batch size过大，不同batch的梯度方向没有任何变化，容易陷入局部极小值。

讲讲正则化为什么能降低过拟合程度，并且说明下下L1正则化和L2正则化。

正则化之所以能够降低过拟合的原因在于，正则化是结构风险最小化的一种策略实现。

给loss function加上正则化项，能使得新得到的优化目标函数h = f+normal，需要在f和normal中做一个权衡（trade-off），如果还像原来只优化f的情况下，那可能得到一组解比较复杂，使得正则项normal比较大，那么h就不是最优的，因此可以看出加正则项能让解更加简单，符合奥卡姆剃刀理论，同时也比较符合在偏差和方差（方差表示模型的复杂度）分析中，通过降低模型复杂度，得到更小的泛化误差，降低过拟合程度。

L1正则化和L2正则化：

L1正则化就是在loss function后边所加正则项为L1范数，加上L1范数容易得到稀疏解（0比较多）。L2正则化就是loss function后边所加正则项为L2范数的平方，加上L2正则相比于L1正则来说，得到的解比较平滑（不是稀疏），但是同样能够保证解中接近于0（但不是等于0，所以相对平滑）的维度比较多，降低模型的复杂度。

什么是优化器？

一言以蔽之，优化器就是在深度学习反向传播过程中，指引损失函数（目标函数）的各个参数往正确的方向更新合适的大小，使得更新后的各个参数让损失函数（目标函数）值不断逼近全局最小。

随机森林的随机性体现在哪里？

1 随机抽样：一个样本容量为N的样本，有放回的抽取N次，每次抽取1个，最终形成了N个样本。每个样本被选择的概率为1/n,则n次都没被选到的概率为（1-1/n）^n
由基本不等式lim x->+无穷 （1+1/x）^x = e，所以上式等于1/e = 0.367。即随机抽样后能抽到67%左右的样本。
2 随机选择属性：再所有的属性中随机选择一些作为待分裂的属性，然后更具计算选择最好的分裂属性进行分裂。