快速单目三维人手和身体的运动捕捉
快速单目三维人手和身体的运动捕捉


1. 论文简要
人体动作的本质细微差别往往是通过肢体动作和手势的结合来传达的,但现有的单目动作捕捉方法大多侧重于身体动作捕捉而忽略手的部分,或者只关注手的动作捕捉而不考虑身体动作。在本文中提出了FrankMocap运动捕捉系统,可以估计三维人手和身体运动。
代码地址:https://github.com/facebookresearch/frankmocap
2. 背景介绍
将视频中的人类动作数字化的技术在各种应用领域具有巨大的潜力,包括人机交互、社会人工智能和机器人技术。人手和身体姿态对于理解这些场景同等重要,因为人手的高自由度,并且相对于人体形态很小,因此使用专业的动作捕捉系统,也很难捕捉人手的动作。目前主流的方法是构建双手和人体的三维参数模型,然而这些方法依赖于对参数模型的拟合,速度慢达不到实时的应用标准。
本论文提出了一种快速并且准确地估计三维人手和人体姿态的方法,主要的思路:首先基于深度神经网络设计人手和人体模块,然后从RGB图像中回归出人手和人体的三维姿态,最后将姿态同步到SMPLX模型中进行集成,实现全身三维动作捕捉。
3. 相关研究
3D参数人体姿态模型:SMPL模型对人体的高矮胖瘦和人体动作的姿态进行定义,对人体每个可以活动的关节点进行参数化。总体来说SMPL模型是一个统计模型,可以通过两种类型的统计参数对人体进行描述。
- 形状参数(shape parameters): 一组形状参数有10个维度的数值描述人的形状,每个维度可以解释为人体形状的某个指标,比如高矮胖瘦等(维度的大小可由PCA控制)。
- 姿态参数(pose parameters): 一组姿态参数 \(24\times 3\) 描述人体动作姿态,特别说明一下,这里的3不是三维空间坐标,而是该节点针对其父节点的旋转角度的轴角式表达(axis-angle representation).
单张图像的3D人体姿态估计:许多三维人体姿态估计方法都考虑从单幅图像中预测三维人体关键点位置。由于缺少三维关节角和相应长度,这些方法的输出不能直接用于图形应用。目前大部分三维人体姿态估计方法都是采用3D参数模型以二维观测重建一个三维人体姿态。
单张图像的3D人手姿态估计:之前的三维人手位姿估计是通过深度图回归得到的,但是不能广泛用于RGB的场景下。最近的工作主要有两类方法,一类是通过图片和OpenPose类似网络得到2D关节点作为输入然后回归出MANO模型的参数;另一类方法是自己构建3D人手模型,将图片和得到的2D热图输入图神经网络回归出人手模型的顶点。
人手和人体姿态估计的联合:由于缺乏全身的标注数据,之前的方法都依赖于优化方法。SMPL-X模型表示全身模型,通过对二维关键点的拟合优化了模型参数,并附加了身体姿态先验和碰撞补偿等约束条件。
4. 本文方法
本文目的是从单目图像中估计3D身体(躯干和肢体部分)和3D手(左和右手),产生SMPLX模型的参数作为输出,以表示3D身体和人手的姿态。该方法的一个重要方面是在SMPL-X模型中使用不同的专家模块对身体和手位姿进行估计,同时两个模块产生兼容的输出。框架的概述如图下图:
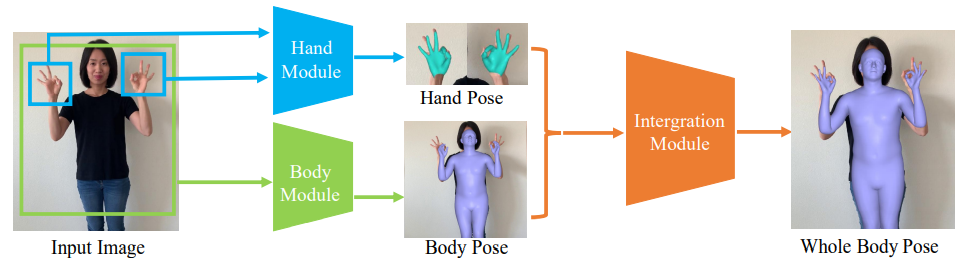
4.1. SMPL-X模型
给定一个单独的图像,本文的方法可以产生SMPL-X模型的形状和姿态参数形式的全身运动捕捉输出。作为SMPL模型的扩展,SMPL-X模型可以表示形状变化,通过低维形状和位姿参数的组合,实现了与姿态相关的人体变形。SMPL模型只关注身体部位,SMPL-X与SMPL模型的一个关键区别在于,SMPL-X还可以通过添加附加组件来表达手指动作和面部表情。
首先用 \(W\) 表示SMPL-X模型:
其中 \(W\) 包含整个身体的全局方向参数 \(\phi_{w} \in \mathbb{R}^{3}\),人体姿态参数 \(\boldsymbol{\theta}_{w} \in \mathbb{R}^{(21+15+15) \times 3}\),身体和人手交叉的形态参数 \(\boldsymbol{\beta} \in \mathbb{R}^{10}\) ,将 \(\boldsymbol \theta_{w}\) 可以分成人体姿态参数 \(\boldsymbol{\theta}_{w}^{b} \in \mathbb{R}^{21 \times 3}\) ,左手姿态参数 \(\boldsymbol{\theta}_{w}^{l h} \in \mathbb{R}^{15 \times 3}\) ,右手姿态参数 \(\boldsymbol{\theta}_{w}^{r h} \in \mathbb{R}^{15 \times 3}\) ,因此 \(\boldsymbol{\theta}_{w}=\left\{\boldsymbol{\theta}_{w}^{b}, \boldsymbol{\theta}_{w}^{l h}, \boldsymbol{\theta}_{w}^{r h}\right\}\)。所有位姿参数表示在运动学模型映射中相对于父关节的相对旋转角度。SMPL-X模型的输出是10745个顶点的mesh结构,\(\boldsymbol V_w \in \mathbb R^{10475\times 3}\) ,利用给定顶点的回归函数 \(R\),可以得到整个身体的三维关节位置:\(\boldsymbol{J}_{w}^{3 D}=R_{w}\left(\boldsymbol{V}_{w}\right)\) ,其中 \(\boldsymbol{J}_{w}^{3 D} \in \mathbb{R}^{(22+15+15) \times 3}\) 。
人手模型通过SMPL-X定义:\(\boldsymbol{V}_{h}=H\left(\boldsymbol{\phi}_{h}, \boldsymbol{\theta}_{h}, \boldsymbol{\beta}_{h}\right)\) 其中 \(\boldsymbol{\theta}_{h} \in \mathbb{R}^{3 \times 15}\) 代表人手姿态参数,\(\boldsymbol{\beta}_h\) 人手模型的形状参数。由于人手模型来自SMPL-X,\(\boldsymbol \beta_h\) 和 \(\boldsymbol \beta_w\) 共享相同的参数化空间。\(\phi_{h} \in \mathbb{R}^{3}\) 代表人手mesh的全局方向,使用人手模型作为独立模型,独立于原始SMPL-X模型的 \(W\) 的祖先节点。人手模型 \(H\) 产生带有778个顶点的人手mesh结构,\(\boldsymbol{V}_{h} \in \mathbb{R}^{778 \times 3}\)。 通过裁剪手腕区域周围的顶点,从整个身体网格 \(V_w\) 来定义的人手网格顶点。3D人手关键点回归可以表示为 \(\boldsymbol{J}_{h}^{3 D}=R_{h}\left(\boldsymbol{V}_{h}\right)\) ,其中 \(\boldsymbol{J}_{h}^{3 D}\in \mathbb{R}^{21\times 3}\) , 包含1个手腕,15个指关节,5个指尖。
该方法的主要优点是三维人手模型的位姿参数、mesh顶点和三维关节点,与全身参数直接兼容,这使人手能够有效地集成全身的模块中。
4.2. 3D人手姿态估计
人手模块结构:人手模型 \(M_{H}\) 由端对端的神经网络构建回归出人手姿态参数,人手模块 \(M_H\) 定义为:
其中 \(I_H\) 表示手部区域的RGB图片,\(c_h=(t_h,s_h)\) 是弱透视相机参数,能够将3D人手模型投影到输入图片上。 其中 \(t_h\in \mathbb{R^2}\) 为图像平面的2D平移,\(s_h \in \mathbb{R}\) 为放缩因子。因此3D人手关键点 \(J^{3D}_{h,i}\) 能正交投影成2D关键点:
人手模型 \(M_H\) 的架构由编码器和解码器结构组成,其中编码器输出来自输入图像的编码特征,以及解码器由特征回归手部位姿参数。编码网络由ResNet-50构成,解码网络由全连接层构成。

训练方法:采用三种不同的标签损失函数:(1) 3D姿态标注(以角度轴表示),(2) 3D关键点标注(关节标注),(3) 2D关键点标注。标签损失分别为 \(L_{\theta}\) ,\(L_{3D}\) ,\(L_{2D}\) ,具体损失函数定义如下:
其中 \(\hat{\theta}_h\) ,\(\hat{J}^{3D}_{h}\), \(\hat{J}^{2D}_h\) 分别为角度轴姿态参数,3D关键点,2D关键点。2D关键点损失对于估计相机投影参数很重要,没有使用3D人手数据集中的形状参数是因为有些数据集采用MANO模型定义与SMPL-X不兼容, 因此采用形状参数的正则损失 \(L_{reg}\) 定义:
用于训练人手模块的总损失 \(L\) 定义如下:
数据集预处理:三维人手姿态数据集通常是在多台不同视角的同步相机平台下拍摄的,用这样的数据集进行训练容易产生过拟合。为解决这一问题可以尽可能多的采用不同数据集来提高模型的泛化性,这种方法会存在不同数据集标签信息不同的问题。(一般通过重新调整3D关键点的顺序)
训练数据增强:在训练期间数据扩充是使模型具有更好泛化能力的常见做法,常见的做法包括随机比例,随机平移,颜色抖动和随机旋转。在自然环境下的视频常常会存在严重的运动模糊,为了提高模型的健壮性,在数据增强过程中加入了运动模型增强,具体做法是生成运动模糊内核,然后用2D滤波器在图片上添加模糊。

4.3. 3D人体姿态估计
人体模块 \(M_B\) 产生躯干和肢体参数:\([\phi_b,\theta_b,\beta_b,c_b]=M_B(I_b)\) ,\(I_b\) 表示图片输入,\(\phi \in \mathbb R^3\) 表示整体身体方向,\(\theta_b \in \mathbb{R}^{21\times 3}\) 表示人体姿态参数(没有人手关键点),\(\beta_b\in \mathbb{R}^{10}\) 表示形状参数。\(\beta_b\) 与 \(\beta_w\) 共享相同的参数空间。
4.4. 整合全身
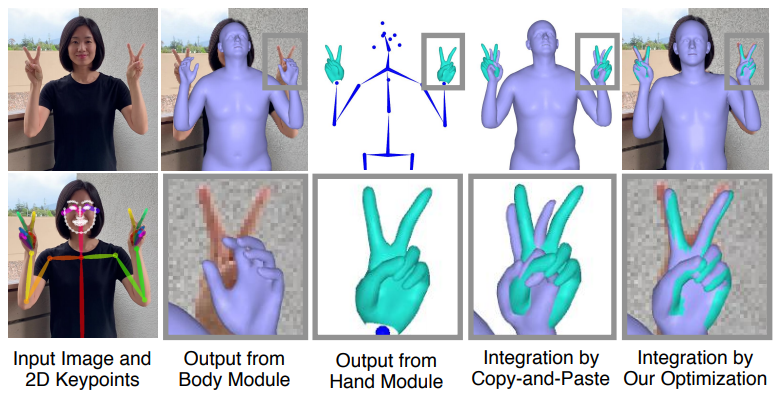
集成模块将3D人体和人手模块的输出统一表示为SMPL-X模型的一种形式。对于整合有两种策略:(1)简单的复制粘贴模式;(2)采用优化框架,包括额外的2D关键点。
复制粘贴模式:由于人手和人体模块的输出与SMPL-X模型兼容,它们可以很容易地组合。一个简单的策略就是从人手和人体各模块的输出中传递相应的关节角度参数。但是,手腕部分需要额外的处理,因为从身体和人手模块获得两个不同的输出。手腕关键点的姿态参数为 \(\theta^{wrist}\) , \(\boldsymbol{\theta}_{b}=\tilde{\boldsymbol{\theta}}_{b} \cup\left\{\boldsymbol{\theta}_{b}^{\mathrm{rwrist}}, \boldsymbol{\theta}_{b}^{\mathrm{lwrist}}\right\}\) , 其中 \(\tilde{\boldsymbol{\theta}}_{b}\) 除了手腕包含所有人体姿态参数。因此整个人体和人手模块以复制粘贴方式整合为:
其中\(\Gamma_{l}\) , \(\Gamma_{r}\) 函数表示将从人手模块得到的全局手腕方向 \(\phi_h\) 转化为局部手腕姿态参数。 这种方式不需要额外的计算量适合实时系统。
优化方式:作为另一种集成方法,建立了一个优化框架来拟合全身模型参数。该策略特别有助于减少复制-粘贴策略手腕部位周围的伪影,也可以利用二维关键点估计输出来提高二维定位质量。优化框架的损失函数为:
其中 \(\mathcal{F}^{2 d}\) 为二维重投影损失项,\(\mathcal{F}^{p r i}\) 作用是保持3D姿态参数和形状参数在合适的空间。
5. 实验论证
5.1. 实验细节
目标框:采用OpenPose获取目标框,
人手模块:ResNet-50
人体模块:SPIN、SMPL
5.2. 数据集
人手数据集:FreiHAND、HO-3D、MTC、STB、RHD、MPII+NZSL
人体数据集:COCO、Human3.6M
5.3. 评估
人手效果的比较:

全身效果的比较:


6. 结论
本文介绍了一种名为FrankMacop的快速运动捕捉系统,我们设计的身体和人手专家模块产生兼容的输出作为全身运动捕捉,并且提出了两种集成策略,快速复制粘贴和优化框架。本文的全身动作捕捉系统在现场演示中,接近实时的速度(9.5 fps),这是比其他方法快几个数量级。
该方法仍然存在一些局限性:(1)如果两只手靠的太近,则手部姿势容易估计错误。(2)需要边框推断出3D的身体和人手。未来的扩展的方向可以处理多人交互的情况,如两个人打招呼时握手。



