手机实时视频去噪(Google Pixel2)
Real-Time Video Denoising On Mobile Phones
Abstract
提出了一种基于移动平台的实时视频去噪算法。基于高斯-拉普拉斯金字塔分解,我们的解决方案的主要贡献是快速对齐和一个新的插值函数,融合有噪声的帧得到去噪的结果。该插值函数对输入帧的局部和全局特性具有自适应能力,对运动对齐误差具有鲁棒性,并且能够高效计算。结果表明,该算法具有相当的质量,离线高质量视频去噪的方法,但是是命令级快。在现代移动平台上,我们的工作用不到20ms的时间处理一个高清帧,并实现公共基准测试的最高分。
关键词:视频去噪,实时处理,移动平台,金字塔分解
1. Introduction
手机摄像由于其便利性已经成为我们日常生活的一部分。手机摄像头用于记录、视频聊天,甚至是直播。然而,移动视频的质量仍然不如专业相机拍摄的视频,尤其是在弱光条件下。移动成像传感器体积小、噪声大,单帧空间去噪方法难以去除时间噪声。尽管视频包括了时间用于有效去噪的信息,高级视频去噪算法对于移动电话来说太慢了:它们中的大多数甚至在台式机上都不是实时的(第2部分)。
本文提出了一种高效的时域去噪方法。首先,我们提出一种新的非线性滤波器来处理空间变化的噪声和运动补偿误差。其次,我们证明了一个优化的onetap时间递归滤波可以达到有竞争力的去噪质量。第三,我们设计的运动估计和过滤块,使他们共享的大部分计算使用一个共同的图像金字塔表示。
我们的算法可以在现代移动平台上实现30+ fps高清分辨率的性能,去噪质量可与最先进的离线方法相媲美。我们将提出的算法集成到Google Pixel 2的图像处理流水线中,该图像处理流水线在公共DxO基准[1]上获得了最高的视频质量评级。
2. Background
视频去噪是一个已经被广泛研究的成熟课题,本文仅对相关工作进行简要回顾。早期的方法扩展了非局部方法[2]、双边滤波[3]或小波去噪[4],但没有明确考虑帧或目标运动。VBM3D[5]和VBM4D[6]通过时序块对齐和分组对BM3D[7]进行扩展,[8]通过运动补偿对3D DWT进行扩展。一些方法利用密集光流[9,10]进一步改进其结果。
注意,这些方法都不是为实时移动应用程序设计的。即使在桌面,大多数其他技术不能实现实时性能在CIF分辨率(更不用说高清),除非使用强大的GPU。更有效的方法是每帧使用一个对齐的块[11,12,13]。尽管如此,他们需要更多的帧来收集足够的块,并且对于移动视频录制来说仍然太慢。
3. Real-Time Video Denoising
我们的算法有两个主要阶段:计算两个连续帧之间的位移映射的对齐阶段和合并阶段,合并输入帧和前一帧的输出。合并的结果用作下一帧的合并阶段的输入之一。注意,我们的算法不执行空间过滤以节省计算时间,尽管金字塔框架隐含地使其成为一种时空方法。通过适当的对齐,即使是纯递归时间滤波也可以收敛到一个非常低噪声的结果[14]。
流程图如图1所示。将 \(t\) 时刻的帧分解为高斯和拉普拉斯金字塔。高斯金字塔用于对齐(第3.1节),而拉普拉斯金字塔用于合并(第3.2节)。合并后的金字塔被折叠以创建最终的输出。我们使用CPU/GPU实现该算法,并在移动平台上对真实噪声进行建模(第3.3节)。
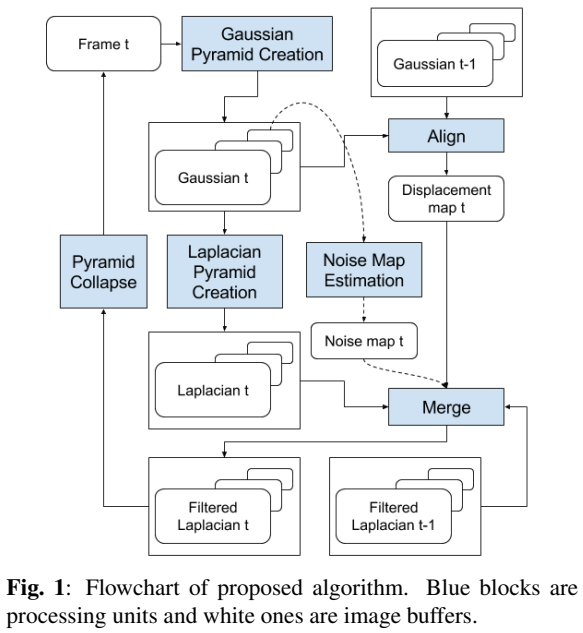
在以下章节中,\(\mathcal{G}^{g}\)表示高斯金字塔级 \(g∈[0,…N_G)\), \(\mathcal{L}^l\)表示拉普拉斯金字塔级\(l\in[0,…, N_G]\) ,和 \(N_G\)和\(N_L\)表示金字塔的高度,和给定金字塔层内的像素位置由 \(p = (x, y)\) 给出,每个拉普拉斯金字塔层的噪声方差图用 \(n^l(p)\)表示。
3.1 Alignment
我们使用分层方法来计算具有大搜索范围的位移图 \(A(p)\)。我们的算法是基于优化后的快速光流方法的[15]。我们还在每个 \(\mathcal{G}^g\)上执行迭代反Lucas-Kanade搜索,但是将运动矢量计算限制在每个维度上步长为16像素的粗网格的顶点上。
在我们的实验中,我们发现在更粗的金字塔层的整数精度的运动矢量足够精确来初始化运动矢量搜索到下一个更细的层。因此,除了最后一层外,我们可以去除所有不必要的插值来计算亚像素对齐误差。最后,为了增加运动搜索范围,减少迭代次数,我们使用最粗层的水平和垂直的一维投影,通过互相关来估计全局运动。我们的优化方法比[15]中的参考方法快4倍。
3.2 Merging
在合并阶段,我们将当前的拉普拉斯金字塔与前一帧的拉普拉斯金字塔合并。我们提出的算法的基础是我们执行IIR预处理(递归滤波器),这意味着我们使用之前滤波后的结果,而不是未处理的前一帧。IIR公式具有较强的去噪性能,但存在潜在的伪影传播缺陷。我们设计插值函数让未对齐错误有更强的鲁棒性,即使在如重影、不存在的特征或过度模糊等错误的情况下也不会引入。
我们首先使用位移图来形成对齐的金字塔 \(L^l_a\),使用前面的金字塔 \(L^l_p\):
其中 \(A^l\) 是 \(A\)在 \(l\) 级缩放版本。
最终的金字塔层 \(L^l_r\) 作为当前层 \(L^l_c\) 和 \(L^l_a\) 的插值:
\(\mathcal{I}_c\) 和 \(\mathcal{I}_p\) 的插值函数适应于像素位置、值和噪声级别。
为了更好地解释插值函数是如何设计的,让我们用 \(\mathcal{L}_{\Delta}^{l}(\mathbf{p})=\mathcal{L}_{c}^{l}(\mathbf{p})-\mathcal{L}_{a}^{l}(\mathbf{p})\) 表示像素值的区别。通过重新整理公式2,我们得到:
其中 \(w^l_c\)为 \(\mathcal{I}_c\) 的最小值,\(w^l_p\) 为 \(\mathcal{I}_p\) 的最大值,\(\mathcal{I}\)为插值因子,决定了当前像素和上一个像素的最终权重。我们将在下面详细解释这些值。
3.2.1 Interpolation bounds \(w^l_c\) and \(w^l_p\)
我们算法中的去噪强度限制定义为 \(w^l_c\) 和 \(w^l_p\)。如果我们设定 \(w_{c}^{l} \leq w_{p}^{l}\),我们可以通过强调之前滤波的成分来获得更强的去噪能力。请注意,因为它们是金字塔级的函数,我们可以选择在某些频段执行更强的去噪,在这些频段,我们更有信心会有更少的由于未对齐错误的伪影。
由于平均,高频特征,如纹理和边缘,有时会得到平滑,即使对齐是几个像素。为了弥补这个问题,我们对插值权值做了一个关键的修改:
用一个因子有效地提高加权平均数略高于1,则可以恢复高频特征保留去噪强度。
在实际应用中,我们对 \(w^l_c\) 和 \(w^l_p\) 进行了自适应调整。对于光线充足的场景,我们可以保留足够的细节而不增强更高的频率,而对于光线昏暗的场景,过度锐化就不那么明显,我们可以安全地提高更高频率的振幅。
3.2.2 Interpolation factor \(\mathcal{I}\)
设计 \(\mathcal{I}\) 是我们算法的关键。该方法考虑了多种时空效应,以最小的伪影达到较好的去噪效果。这是通过考虑预期噪声的数量和两个金字塔值之间的实际差异来实现的。我们还考虑了补丁式对齐错误——对于在前一帧中没有很好的匹配补丁的情况,我们需要更保守一些,以便不向当前帧引入任何伪影。
\(\mathcal{I}\) 的值总是在[0,1]的范围内。从式3中可以看出,\(\mathcal{I}\) 越高,去噪强度越低,前一帧的贡献越小。我们计算两个插值因子候选并选择较大的一个: \(\mathcal{I}=\max \left(\mathcal{I}_{e}, \mathcal{I}_{\Delta}\right)\) ,其中 \(\mathcal{I}_e\) 基于对齐误差,\(\mathcal{I}_{\Delta}\) 基于像素区别。
在精度较好的区域,\(\mathcal{I}_∆\) 优于 \(\mathcal{I}_e\)。对于这样的像素,我们可以自信地在当前金字塔和以前的金字塔之间进行插值。然而,在对齐误差较大的领域,\(\mathcal{I}_e\) 将占主导地位:
其中 \(A^l_e(p)\) 为对齐阶段的块匹配误差。调谐参数 \(C_e\) 设置了可接受的运动对准误差的限度。\(\mathcal{I}_e\) 还关闭了由于遮挡、物体进出帧等引起的粗对准误差区域的去噪。
对于\(\mathcal{I}_∆\),一个流行的选择是众所周知的维纳滤波器:
该方法已在多帧傅里叶和小波去噪中得到应用[13,16],在对准精度较高的情况下取得了较好的效果。然而,由于场景的动态性较高和视频录制的计算预算有限,通常情况下对齐置信度较低,而且由于对对齐误差的预测,我们不得不更加保守。因此,我们提出了一种新的插值器,它也依赖于噪声方差和像素值之间的差异,但有一个'sigmoid'形代替:
其中m为中点(即插值因子为0.5 当 \(|L^l_∆((p)| = m(p))\) 时,\(C_{middle}\) 为定义边界弯曲(中间)点和 \(C^l_{noise}\) 是不同金字塔等级噪声的缩放常数。
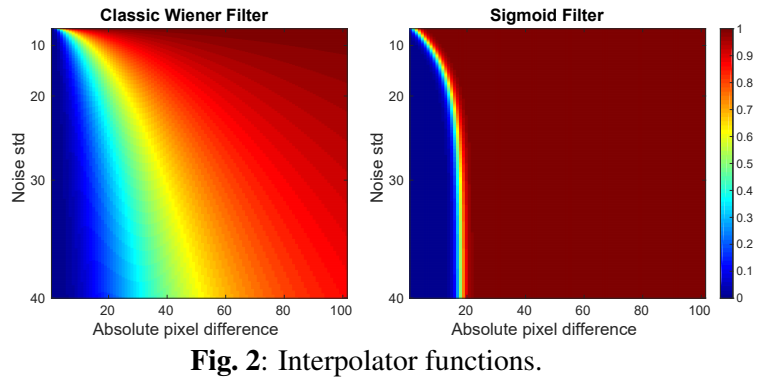
不同噪声水平下 \(\mathcal{I}_{Wiener}\) 和 \(\mathcal{I}_{∆}\) 值及绝对像素差见图2。即使有低噪声水平和高像素差异, \(\mathcal{I}_{Wiener}\) 仍然允许前一个像素对结果做出显著贡献,并导致重影或过度平滑的伪影。

另一方面, \(\mathcal{I}_{∆}\) 有一个急剧的相变。它通过允许插值因子在比 \(\mathcal{I}_{Wiener}\) 更大的值范围内接近0,从而在更高的噪声水平上应用更强的去噪。然而,即使对于非常高的噪声水平,较大的像素差异也主要是由于错误的比对而不是噪声造成的,并且 \(\mathcal{I}_{∆}\) 快速地阻止了来自前一帧的贡献,以避免伪影。图3清晰地显示了提出的\(\mathcal{I}_{∆}\)相对于 \(\mathcal{I}_{Wiener}\) 抑制了伪影,同时在帧的其余部分保持了相同的去噪水平。
当所有的拉普拉斯金字塔层 \({\mathcal{L}^l_r}\) 都去噪之后,我们只需将它们折叠到输出帧中,并将它们存储为下一帧的\({\mathcal{L}^l_p}\)。
3.3 Implementation Details
我们使用CPU/GPU协同处理来实现我们的算法,并在桌面和使用高通骁龙835的谷歌Pixel 2上进行测试。我们在GPU上实现了用于金字塔创建和合并的OpenGLES 着色器,并使用Halide[17]在CPU上实现了对齐和噪声估计。虽然只有CPU的实现仍然可以实现实时吞吐量,但我们的联合CPU/GPU解决方案大大降低了功耗(- 66%)。我们发现现有的空间去噪器对于色度信道是足够有效的,并且只能在luma信道上实现我们的算法。
3.3.1 Noise Estimation
实际噪声特性随传感器和场景属性[18]的不同而不同,正确的噪声建模是降噪[13]的关键。我们通过在每一层的每一个像素提供噪声映射 \({n^l}(p)\) 来对噪声方差进行建模。
在我们的目标平台中,我们使用控制照明和相机设置来校准传感器噪声,并确定图像处理阶段(镜头阴影校正、白平衡、颜色空间转换、色调映射、伽玛校正等)如何转换图像和噪声方差。在捕获时,利用相机设置的辅助信息,将最粗的 \(\mathcal{G}^g\)层反变换回原始的传感器域,并对传感器噪声进行变换,得到\({n^l}(p)\)。
4. Results
将我们的方法与最先进的方法相比较是另一个挑战。我们开发了一个应用于移动商业产品的算法,由于非常严格的计算、功率和内存预算,因此其性能与学术解决方案相比可能会有些不足。另一方面,其他商业解决方案只能以最终的系统形式提供给我们,即我们不能通过向各种算法提供完全相同的输入并对结果进行评估来执行标准测试。因此,我们提供了各种设置:实验室测试、真实世界的评估以及商业基准协议。

在实验室实验中,我们在一个包含彩色棋盘静态场景的三脚架上录制了一个短视频(74帧,1080p分辨率),并使用所有帧的时间平均值作为ground truth。除了我们自己的算法,我们还对这个视频应用了三个有代表性的时域去噪算法:VBM3D [5], 3DWF[11,12],以及HDR+[13]。在表1中,我们列出了运行时间以及图4中突出显示的平坦区域的平均PSNR和时间方差。在经过评估的算法中,VBM3D获得了最好的质量,但是使用强大的桌面CPU (HP z840工作站中的Intel Xeon E5)处理一帧需要几秒钟的时间。该方法在单线程Google Pixel 2 (Qualcomm Snapdragon 835)上实现了数量级的速度提升和可持续的实时性能。同时,我们的方法在峰值信噪比和时间方差方面都取得了很好的竞争结果。

图5显示了由Pixel 2记录的低光视频的真实世界样本。请注意,这些比普通的实验室测试更具挑战性:手机是手持的,没有三脚架,场景可以包括移动的物体,照明条件可能会有所不同。该方法可以在不影响细节的情况下,大大降低这些情况下的噪声。
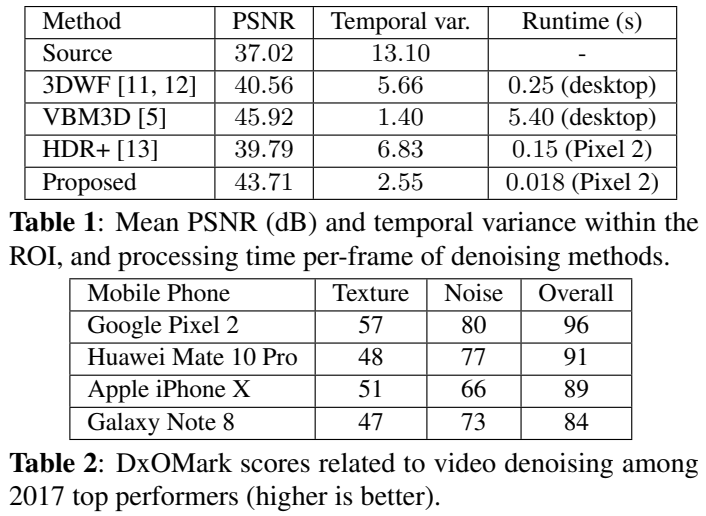
最后,我们在表2中列出了公共DxO基准测试结果。DxO实验室在不同的场景(图表、自然物体、自拍、团体拍摄……)和不同的照明条件(步行、平移、户外、室内、非常低的光照条件、高动态范围……)下进行实验室和现场测试,并将几种主观和客观指标结合在一起,形成一份报告[19,1]。它是最流行的手机相机质量评估基准。我们可以看到Pixel 2获得了最高的视频噪声评分,并且比其他手机保存了更多的纹理,这些手机都有自己专有的空间和时间去噪解决方案。整体视频评分在2017年所有高端智能手机中是最高的。
5. Reference
[1] “DxOMark mobile test protocol and scores,” www.dxomark.com/ dxomark-mobile-testing-protocol-scores/, Accessed: 2018-01-18.
[2] M. Mahmoudi and G. Sapiro, “Fast image and video denoising via nonlocal means of similar neighborhoods,” IEEE Signal Processing Letters, vol. 12, no. 12, pp. 839–842, 2005.
[3] E. P. Bennett and L. McMillan, “Video enhancement using per-pixel virtual exposures,” in ACM TOG, 2005, vol. 24, pp. 845–852.
[4] H. Malm, M. Oskarsson, E. Warrant, P. Clarberg, J. Hasselgren, and C. Lejdfors, “Adaptive enhancement and noise reduction in very low light-level video,” in ICCV, 2007.
[5] K. Dabov, A. Foi, and K. Egiazarian, “Video denoising by sparse 3d transform-domain collaborative filtering,” in 2007 15th European Signal Processing Conference, 2007, pp. 145–149.
[6] M. Maggioni, G. Boracchi, A. Foi, and K. Egiazarian, “Video denoising, deblocking, and enhancement through separable 4-D nonlocal spatiotemporal transforms,” IEEE TIP, vol. 21, no. 9, pp. 3952–3966, 2012. [7] K. Dabov, A. Foi, V. Katkovnik, and K. Egiazarian, “Image denoising by sparse 3-D transform-domain collaborative filtering,” IEEE TIP, vol. 16, no. 8, pp. 2080– 2095, 2007.
[8] S. Yu, M. O. Ahmad, and M. Swamy, “Video denoising using motion compensated 3-D wavelet transform with integrated recursive temporal filtering,” IEEE TCSVT, vol. 20, no. 6, pp. 780–791, 2010.
[9] C. Liu and W. T. Freeman, “A high-quality video denoising algorithm based on reliable motion estimation,” in ECCV, 2010, pp. 706–719.
[10] A. Buades, J. L. Lisani, and M. Miladinovic, “Patchbased video denoising with optical flow estimation,” IEEE TIP, vol. 25, no. 6, pp. 2573–2586, 2016.
[11] A. Kokaram, “3D Wiener filtering for noise suppression in motion picture sequences using overlapped processing,” in Signal Processing V, Theories and Applications, 1994, pp. 1780–1783.
[12] A. Kokaram, D. Kelly, H. Denman, and A. Crawford, “Measuring noise correlation for improved video denoising,” in ICIP, 2012, pp. 1201–1204.
[13] S. W. Hasinoff, D. Sharlet, R. Geiss, A. Adams, J. T. Barron, F. Kainz, J. Chen, and M. Levoy, “Burst photography for high dynamic range and low-light imaging on mobile cameras,” ACM TOG, vol. 35, pp. 192:1– 192:12, 2016.
[14] T. Hachisuka, S. Ogaki, and H. W. Jensen, “Progressive photon mapping,” ACM TOG, vol. 27, no. 5, pp. 130:1– 130:8, 2008.
[15] T. Kroeger, R. Timofte, D. Dai, and L. Van Gool, “Fast optical flow using dense inverse search,” in ECCV, 2016, pp. 471–488.
[16] V. Zlokolica, A. Pizurica, and W. Philips, “Waveletdomain video denoising based on reliability measures,” IEEE TCSVT, vol. 16, no. 8, pp. 993–1007, 2006.
[17] J. Ragan-Kelley, A. Adams, S. Paris, M. Levoy, S. Amarasinghe, and F. Durand, “Decoupling algorithms from schedules for easy optimization of image processing pipelines,” ACM TOG, vol. 31, no. 4, pp. 32:1–32:12, 2012.
[18] C. Liu, R. Szeliski, S. B. Kang, C. L. Zitnick, and W. T. Freeman, “Automatic estimation and removal of noise from a single image,” IEEE TPAMI, vol. 30, no. 2, pp. 299–314, 2008.
[19] F. Cao, F. Guichard, and H. Hornung, “Dead leaves model for measuring texture quality on a digital camera,” in Digital Photography, 2010, p. 75370.



