基于空间熵的全局和局部图像对比度增强

目录

• 摘要
• 1. 介绍
• 2. 相关工作
• 3. 空间熵的对比度增强
  • A. 灰度全局对比度增强
  • B. 灰度全局和局部的对比度增强
  • C. 颜色恢复
• 4. 实验结果
  • A. 数据集，算法和定量检测
  • B. 定性评估
  • C. 对比度增量的定量检测
  • D. 定量评定
  • E. 对比度增强对目标识别的影响
  • F. SECEDCT对比度增强的程度
  • G. 计算时间
• 5. 结论
• 参考文献

Spatial Entropy-Based Global and Local Image Contrast Enhancement

github地址：https://github.com/xiezhongzhao/Contrast_Enhancement
安卓版本代码地址：https://github.com/xiezhongzhao/ImageEnhancementAndroid

摘要

该文章提出了一种利用像素空间信息增强输入图像对比度的方法。该算法是一种利用像素灰度空间分布计算像素空间熵的新方法。与传统方法不同的是，该算法考虑的是图像灰度空间位置的分布，而不是灰度分布或从图像灰度计算出的联合统计量。 对于每个灰度级，使用具有相同灰度级的所有像素的空间位置直方图计算相应的空间分布。通过计算图像灰度空间分布的熵值，得到一个分布函数，再将其映射成均匀分布函数，实现最终的对比度增强。 该方法在低对比度图像的情况下实现了对比度的改善; 并且如果图像的对比度足够高，它不会改变图像。因此，它总是在不失真的情况下产生令人愉悦的视觉效果。该方法与变换域系数加权相结合，实现了局部和全局对比度增强。局部对比度增强的程度是可以控制的。进行了若干对比增强效果的实验。实验结果表明，与现有的几种增强算法相比，本文提出的算法能产生更好的增强图像。

关键词：对比度增强，空间熵，图像质量增强，离散余弦变换。

1. 介绍

对比度增强是用来增加一个低动态范围的图像的对比度或显示图像细节，否则将被隐藏的[1]。由于灰度差异，增强后的图像在质量上看起来比原来的图像要好。对象和背景之间的对比度增加。它通常被用作大多数图像处理/计算机视觉算法的预处理。

一般来说，设计一种无视觉伪影的对比度增强方法是比较困难的。考虑到这一点，我们提出了一种全局的、计算效率高的空间对比度增强方法，该方法使用图像的灰度空间位置进行增强，而不是直接使用灰度或它们的共现。 一张图片的灰度空间位置分布的互信息用于获得一个函数，该函数进一步映射到均匀分布以实现对比度增强。 提出的全局对比度增强算法命名为“基于空间熵的对比度增强(SECE)”。 SECE在没有任何参数选择的情况下产生自然的全局对比度增强效果。 此外，与原始直方图相比，该算法没有改变处理后的直方图的信息结构。因此，考虑到原始图像在没有明显失真的情况下有对比度改进的余地，它会产生自然的增强效果。 据我们所知，这是第一次提出这种新的空间熵定义并用于对比度增强。为了同时实现全局和局部的对比度增强，先对SECE全局增强的图像的变换域(2D离散余弦变换形式(2D-dct))系数进行加权，然后进行逆变换(逆2D-DCT)以获得全局和局部增强对比度的输出图像。 该方法能够在不需要任何视觉伪影的情况下同时执行全局和局部对比度增强。这个算法被命名为“基于空间熵的DCT(SECEDCT)对比度增强”。SECEDCT是SECE的一般化形式，可以控制局部对比度增强的程度。因此，零水平的局部对比度增强将SECEDCT转换为SECE。

论文组织如下。第二部分为相关工作的文献综述。第三部分给出了空间熵的一个新的定义，并介绍了提出的对比度增强算法。第四节用最先进的对比度增强算法对所提出的算法进行了定性和定量的比较。第五部分是本文的结论。

2. 相关工作

对比增强算法可根据应用于[2]的数据域分为两大类: 1）变换域算法；2）图像域算法。变换域算法将输入图像分解成不同的子带，从而在全局或局部修改图像数据[3]-[8]所需频率分量的大小。 这些算法通过转换适当的子带和在适当的尺度上实现同时的全局和局部对比度增强。该算法计算复杂，为了避免图像退化，需要对相关参数进行适当的设置。例如，中心环绕Retinex[3]算法是为了实现图像的亮度和颜色恒常性而开发的，其中恒常性是指对颜色和亮度的感知不受空间颜色和光照的影响。 增强后的图像具有不依赖于场景光照空间分布的压缩动态范围和颜色的优点。增强后的图像具有不依赖于场景光照空间分布的压缩动态范围和颜色的优点。 然而，增强后的图像可能会包含“光晕”现象，特别是沿着大型均匀区域之间的边界。“变灰”也会发生，导致场景的图像趋于中灰色。 在[4]-[6]中，提出了三种不同的变换域(离散余弦变换)对比度增强算法: a)对数变换his-togram matching (LTHM)， b)对数变换直方图移位(LTHS)， c)对数变换直方图整形使用高斯分布(LTHSG)。 一般情况下，变换域系数是根据变换域系数分布到目标分布的映射进行修正，然后进行反变换(反离散余弦变换)得到对比度增强图像。 在LTHM中，目标分布是通过直方图均衡化的输入图像的变换域系数分布得到的。输入图像的变换域系数分布的移位形式作为目标分布LTHSG的目标分布采用LTHS和一个均值和标准差的高斯分布。 后一种算法需要选择直方图移位参数和高斯分布的均值和标准差，这对计算有很大的要求。同时，LTHM是一个自由参数，其结果与其他[6]是可比较的。LTHM的目的是模拟直方图均衡化的能力，而不受动态范围过度扩展的副作用。 这种方法有一个明显的优点，就是非常快，没有内置的递归，这使得它成为一种简单快速的基于变换直方图的图像增强解决方案。 但是，由于在变换域使用全局直方图均衡化的图像的直方图作为目标直方图，仍然可以观察到全局直方图均衡化所产生的视觉伪影。第二代小波也被用来产生没有“光晕”伪影的增强图像。 在基于边缘避免小波的对比度增强算法(EAW)[8]中，对变换域的小波系数进行了修正，并应用逆变换得到对比度增强图像。该方法通过适当的参数选择，同时实现了全局对比度增强和局部对比度增强。

尽管变换域对比度增强算法在许多问题领域都显示出良好的效果，但由于其计算性、内存和适当的参数设置要求，图像域对比度增强算法得到了广泛的应用。 增强图像对比度的传统方法是根据特定的目标直方图来处理单个像素的灰度级。目前应用最广泛的图像域对比度增强算法global histogram equaliza- b0 (GHE)[1]采用输入图像直方图的累积分布函数(CDF)与均匀分布的CDF匹配得到的输入-输出映射。 GHE虽然利用了图像的可用动态范围，但如果直方图中有较大的峰值，则会过度增强图像，导致图像变得粗糙和 增强图像的噪声外观。 为了解决上述问题，人们开发了局部直方图均衡化(LHE)算法，如[9]。这些算法使用一个小窗口，在每个图像像素上依次滑动，并且使窗口当前位置内像素的直方图相等。除了计算方面的问题，LHE有时会过度增强图像的某些部分和任何噪声，并可能产生不希望的棋盘效果。人类视觉系统(HVS)也被用来缓解脑缺血再灌注的arti- facts和改善感知的对比度[10]-[12]。将图像分割成三个区域将基于hvt的阈值化和图像均衡化应用于每一段。经过处理的区域与一个加权相结合，以创建最终的增强图像。 该算法的阈值和合并阶段取决于几个阈值，这些阈值必须由视觉观察者和/或输出图像相对于参数的对比度度量的局部最小值仔细选择。这些参数都是实值，选取它们的计算量很大，使得该算法难以应用。

GHE的计算效率促使研究人员创造方法来减轻其伪影。针对改进后的GHE[13] -[15]的几种算法可以获得满意的对比度增强效果。GHE应用直方图规范，通过适当地将图像直方图更改为所需的直方图来获得对比度增强。 他假设目标直方图是均匀分布的。然而，GHE未能提供有效的直方图规范。精确的his- togram specification (EHS)[13]保证了增强后得到的图像直方图几乎完全符合要求。 然而，对于期望的直方图并没有任何明显的选择，大多被认为是单形式的。虽然EHS可以用来获得均匀分布的输出直方图，但这并不能保证输出不受视觉伪影的影响。 在[14]中进行直方图均衡化之前，对原始图像直方图进行加权和阈值化处理。加权和阈值化是通过将原始图像直方图夹在一个上阈值和一个下阈值处，并使用带索引的归一化幂律函数转换这些阈值之间的所有值来完成的。 我们将该算法称为加权阈值直方图均衡化。WTHE通过精心选择的默认参数设置提供了令人满意的增强。直方图修改框架(HMF)[15]中的对比度增强使计算目标直方图的参数化代价函数最小化。该代价函数由直方图偏离原直方图和均匀直方图的最小的惩罚项和直方图的平滑性组成。此外，边缘信息被嵌入到成本函数中，以对区域边界周围的像素进行加权，从而解决噪声和黑白拉伸[15]问题。不同的参数设置会导致不同的对比度增强。与WTHE相似，加权分布自适应伽马校正(AGCWD)[16]通过加权分布对输入直方图进行修改，并利用伽马校正对图像进行自动增强，但是当输入直方图中出现高峰值时，该算法可能会导致图像亮部的细节丢失。 利用高斯混合模型(GMM)将图像的离散直方图变换为连续分布，利用最终的GMM分量获得输入直方图[17]的子区域。 将非线性映射应用于每个子区域以找到最终的转换。虽然这一过程可能会导致感知对比度的改善，但算法的计算要求很高。

最近，一种利用每个像素的上下文信息来增强输入图像对比度的二维直方图均衡化(2DHE)算法被提出。他为对比度增强开辟了一个不同的方向。该算法通过增加图像中每个像素与相邻像素之间的灰度差来改善图像的对比度。 对于给定的图像，像素与相邻像素之间灰度差的模量是均匀分布的。 GHE是2DHE在上下文信息未被利用时的一个特例。2DHE中需要调整的参数是空间邻域支持的大小，它为给定的增强图像动态范围提供上下文信息。之后，进一步改进了二维直方图的思想，实现了上下文和变分对比度增强(CVC)[18]。通过最小化与二维输入直方图差异的Frobenius范数的参数化和，得到平滑的二维目标直方图二维均匀分布直方图。 对比度增强是通过将二维输入直方图的对角元素映射到二维目标直方图的对角元素来实现的。虽然与参数相关的结果是令人满意的，但是该方法在创建a时需要大量的计算二维直方图。该方法进一步改进，以牺牲较高的计算成本[19]为代价，使考虑图像不同因素的复杂目标函数最小化。

一般来说，基于二维直方图的[2]、[18]、[19]方法产生的输出结果比仅使用一维直方图的方法产生的视觉失真更小。然而，创建一个二维的直方图是需要计算的，这种需求随着周围[18]大小的增加呈指数增长。此外，上述方法都是在不考虑图像对比度的情况下进行对比度增强的。这可能导致退化的对比度情况下，图像有高的对比度。此外，大多数图像处理/计算机视觉算法通常使用对比度增强方法作为预处理步骤，因此该算法应该能够在其默认参数下提供令人满意的结果。 虽然精心选择的参数有助于产生满意的结果，为上述增强算法，这些参数可能必须适应图像的图像。

3. 空间熵的对比度增强

A. 灰度全局对比度增强

1）问题定义：假定一张输入图像为 \(X=\{x(i, j) | 0 \leq i \leq H-1,0 \leq j \leq W-1\}\)，图片大小为 \(H\times W\)，其中\(x(i,j)\in[0,\mathbb{Z}^{+}]\)，假定\(X\)有动态范围\([x_d,x_u]\)，像素值\(x(i,j)\in[x_d,x_u]\)。 基于空间熵的对比度增强(SECE)算法的目标是生成看起来自然的增强图像 \(Y=\{y(i,j)|0\leq i \leq H-1,0 \leq j \leq W-1\}\) 。 \(Y\)的动态范围可以拉伸或压缩到区间内\([y_d,y_u]\)，其中 \(y(i,j)\in [y_d,y_u]\)，\(y_d<y_u\)和\(\{y_d,y_u\}\in[0,\mathbb{Z}^+]\)。 在这项工作中，增强图像利用了整个动态范围 ：例如对于8位图像\(y_d=0\)，\(y_u=2^8-1=255\)。

2） 灰度图像的空间直方图 ：将 \(\mathcal{X}=\left\{x_{1}, x_{2}, \ldots, x_{K}\right\}\) 作为图像 \(X\) 存在的 \(K\) 个灰度级的集合，其中 \(x_1<x_2<...<x_k\)， 计算 \(X\) 的空间网格上灰度级 \(x_k\) 的二维空间直方图为:

\[h_k=\{h_k(m,n)|1\leq m \leq M, 1\leq n\leq N\}\space (1) \]

其中 \(m,n\in \mathbb{Z}^+\)，\(h_k(m,n)\in[0,\mathbb{Z}^+]\) 是在空间网格中定位在图像区域 \([(m-1)\frac{H}{M},m\frac{H}{M}]]\times [(n-1)\frac{W}{N},n\frac{W}{N}]\) 灰度 \(x_k\) 出现的次数。二维直方图上的网格总数为 \(MN\) ，利用不同灰度级的个数 \(K\) 和比率 \(r=\frac{M}{N}=\frac{H}{W}\):

\[N=\left\lfloor (\frac{K}{r})^{1/2} \right\rfloor, M=\left\lfloor(K r)^{1 / 2}\right\rfloor \space (2) \]

其中符号 \(\left\lfloor . \right\rfloor\) 表示取最近的整数，在形成灰度 \(x_k\) 的二维空间直方图 \(h_{k}\) 时，在空间网格上保护原始图像的长宽比。这样在形成二维空间直方图时，可以保护像素的空间特征。

3) 空间熵与分布函数: 根据二维空间直方图 \(h_{k}\)，计算灰度级 \(x_{k}\) 的熵测度 \(s_{k}\) :

\[S_k=-\sum_{m=1}^{M}\sum_{n=1}^{N}h_k(m,n)log_2(h_k(m,n)) \space (3) \]

公式3可以用来计算离散函数 \(f_k\) :

\[f_{k}=S_{k} / \sum_{l=1, l \neq k}^{K} S_{l} \space (4) \]

离散函数 \(f_{k}\) 衡量的是灰度 \(x_{k}\) 相对于其余的灰度级 \(x_l, l\neq k, l=1,...,K\) 的相对重要性， 对离散函数 \(f_k\) 进一步归一化:

\[f_{k} \leftarrow f_{k} / \sum_{l=1}^{K} f_{l} \space (5) \]

累积分布函数 \(F (k)\) 定义如下:

\[F_{k}=\sum_{l=1}^{k}f_l \space (6) \]

4) 映射函数: 利用累积分布函数 \(F_k\)，将 \(x_k\) 映射到 \(y_k\):

\[y_{k}=\left \lfloor F_{k}(y_u-y_d)+y_d \right \rfloor \space (7) \]

B. 灰度全局和局部的对比度增强

SECE是为全局对比度增强而设计的，因此一个单一的传递函数应用于整个图像。该算法对输出图像进行对比度增强，且不产生明显的失真。为了实现全局和局部对比度增强，我们开发了一种自动算法(SECEDCT)，该算法同时使用SECE全局对比度增强算法和2D-DCT局部对比度增强算法。SECEDCT算法流程如图2所示。该算法由以下步骤组成，具体如下: 使用SECE进行全局对比度增强、二维离散余弦变换(2D-DCT)，变换域系数加权，以及二维离散余弦变换反变换。

SECEDCT在2D-DCT的变换域中进行操作。该算法首先使用SECE进行全局对比度增强，然后进行2D-DCT变换[1]。图片 \(X=\{x(i, j) | 0 \leq i \leq H-1,0 \leq j \leq W-1\}\) 的二维离散余弦变换产生的相同大小的变换图片\(D=\{d(k,l)|0 \leq k \leq H-1, 0 \leq l \leq W-1\}\) :

\[\begin{aligned} d(k, l)=& c_{k} c_{l} \sum_{i=0}^{H-1} \sum_{j=0}^{W-1} x(i, j) \cos \left(\frac{\pi(2 i+1) k}{2 H}\right) \\ & \times \cos \left(\frac{\pi(2 j+1) l}{2 W}\right) \end{aligned} \space (8) \]

其中 \(c_k\) 和 \(c_l\) 如下定义：

\[c_{k}=\left\{\begin{array}{l}{\sqrt{\frac{1}{H}}, k=0 ;} \\ {\sqrt{\frac{2}{H}}, 1 \leq k \leq H-1}\end{array}, \quad c_{l}=\left\{\begin{array}{l}{\sqrt{\frac{1}{W}}, l=0} \\ {\sqrt{\frac{2}{W}}, 1 \leq l \leq W-1}\end{array}\right.\right. \space (9) \]

指标 \(k\) 和 \(l\) 的高值代表高频率分量，反之亦然。为了增加局部对比度，需要增加更高的频率变换系数。从而对变换域系数 \(d (k,l)\) 进行修正:

\[\hat{d}(k,l)=w(k,l)d(k,l) \space (10) \]

其中 \(w(k,l)\in \mathbb{R}\)为加权系数，加权系数为更高的频率分配更高的系数，反之亦然，定义如下:

\[w(k, l)=\left(1+\frac{\alpha-1}{H-1} k\right)\left(1+\frac{\alpha-1}{W-1} l\right) \space (11) \]

在 \(\alpha >= 1.0\) 代表增强。\(\alpha\) 的值越高，局部增强程度也就越高。然而，$\alpha $ 值越高也导致像素饱和。因此一个自动选择 $ \alpha $ 是很重要的。在该算法中，$ \alpha $ 根据公式（5）熵估计计算如下：

\[\alpha=\left(\sum_{k=1}^{K} f_{k} \log _{2}\left(f_{k}\right)\right)^{\gamma} \space (12) \]

其中 \(\gamma \in[0,1]\) 决定局部对比度增强的程度 ，例如当 \(\gamma=0\) 时，只有全局增强没有局部增强， 因此输出将与SECE的输出完全相同。 为最大化局部增强,可以选择 \(\gamma = 1\)。值得注意的是 \(w(0,0) = 1\)，这保证了图像的平均值不会发生显著变化。\(\gamma = 0.5\) 的默认值是用于这项工作除非另有说明。

将变换域系数按公式式(10)加权后，应用2D-DCT反变换[1]得到全局增强图像和局部增强图像 \(Y=\{y(i,j)|0\leq i \leq H-1,0 \leq j \leq W-1\}\) :

\[\begin{aligned} y(i, j)=& \sum_{k=0}^{H-1} \sum_{l=0}^{W-1} c_{k} c_{l} \hat{d}(k, l) \cos \left(\frac{\pi(2 i+1) k}{2 H}\right) \\ & \times \cos \left(\frac{\pi(2 j+1) l}{2 W}\right) \end{aligned} \space (13) \]

SECEDCT是SECE的广义版本，当 \(\alpha= 1\), 以及 \(\gamma= 0\) 被选中时, \(w (k, l)\) 对于所有 \((k,l)\) 成为 1 和变换域系数保持不变。因此，SECEDCT将生成与输入图像相同的输出图像，而输入图像只不过是经过SECE算法增强的图像。换句话说，\(\gamma= 0\) 意味着只有全局增强但没有局部增强。

图1是一个灰度图像的例子，由GHE和所提出的方法以及相应的直方图产生的增强，如图1所示。从图像中可以看出，GHE对输入图像进行了过度增强，同时SECE对输出图像进行了自然增强。相应的直方图显示，SECE生成的输出直方图保留了输入直方图的形状，输出直方图延伸在整个动态范围内。 因此，它适合于自然地寻找对比度增强，只要输入没有失真。很明显，SECEDCT既能产生全局增强，也能产生局部增强。SECEDCT提供的关于SECE的局部增强图是清晰的。 而且， SECEDCT的直方图显示，它创建了一个可以占据整个动态范围的增强图像。

C. 颜色恢复

将对比度增强扩展到彩色图像的一种方法是只将算法应用于彩色图像的亮度分量（V），并保留彩色分量。选取HSV颜色空间[1]，彩色图像增强实例如图1所示。

4. 实验结果

A. 数据集，算法和定量检测

1）数据集和算法：我们使用来自几个数据集的标准自然测试图像。伯克利500图像数据集（The Berkeley 500 image dataset）[20]是用来定性定量的评估和比较SECE和SECEDCT，与我们的执行GHE, EHS [13]， WTHE [14]，LTHM [4] - [6]，LTHS [4] - [6]， HMF [15]， CVC [18]， 2DHE [2]， AGCWD[16]。 对伯克利数据集[20]的500幅自然图像进行了定量测量的显著性检验。HMF的参数是通过最大化给定输入图像在视觉质量和定量测量方面的性能来设置的。对于EHS、CVC和2DHE，我们使用算法的默认参数设置。

对从“柯达时刻（Kodak Moment of the Day）”相册[21]-[24]和CSIQ图像数据库[25]采集的图像进行了视觉评估测试，该数据库提供了不同类型失真的自然图像。由于这项工作的范围是对比度增强，带有全局对比度衰减的图像被选择并用于定性评估。

2）量化方式： 评估图像增强是不容易的，因为它很难量化 一个改善感知的图像。然而，人们期望增强后的图像的对比度增加，同时其相对于原始图像的视觉感知不失真。因此，我们测量输入和增强图像的对比度，并期望增强图像的对比度增加。同时，对原始图像和增强图像之间的视觉失真进行了测量，期望失真较小。

图像的对比度可以用熵增强的期望度量[6]，[12]来测量。然而，我们观察到\(EMEE\)对噪声高度敏感，可能产生不正确的测量结果，与感知的对比度不匹配。因此，我们稍微修改了\(EMEE\)，并提出了梯度\(EMEG\)增强的期望方法。 将输入图像分成 \(k_1k_2\) 重叠子块 \(X_{i,j}\)，大小为 \(w1\times w2\)。 \(EMEG\)计算为 :

\[E M E G(\mathbf{X})=\frac{1}{k_{1} k_{2}} \sum_{i=1}^{k_{1}} \sum_{j=1}^{k_{2}} \frac{1}{\beta} \max \left(\frac{\mathbf{X}_{i, j}^{d x, h}}{\mathbf{X}_{i, j}^{d x, l}+\epsilon}, \frac{\mathbf{X}_{i, j}^{d y, h}}{\mathbf{X}_{i, j}^{d y, l}+\epsilon}\right) \space (14) \]

其中 \(EMEG(X)\in[0,1]\)，\(\text{max}(.)\) 是选取最大值函数，\(X_{i,j}^{d_{x,h}}\) 和\(X_{i,j}^{d_{x,l}}\) 分别是在块\(X_{i,j}\)的 \(x\) 方向的绝对值梯度的最大值和最小值。\(X_{i,j}^{d_{y,h}}\) 和\(X_{i,j}^{d_{y,l}}\) 分别是在块\(X_{i,j}\)的 \(y\) 方向的绝对值梯度的最大值和最小值。\(\beta\) 是权重系数，\(\epsilon\) 是常量防止分母为0。不同的区块大小 (即\(w1 \times w2\)) 得到不同的 \(EMEG\) 值，我们使用 \(w1 \times w2 = 8 \times 8\)。高对比度子块的\(EMEG\) 值较高，而同质性子块的 \(EMEG\) 值应接近于零。值得注意的是，\(EMEG\) 对噪音非常敏感。例如，如果该算法生成的输出图像在图像的均匀区域上引入了噪声，那么虽然输出图像看起来不自然，但其对应的 \(EMEG\) 值会很高。然而，对于对比度增强算法来说，它的期望至少是 \(EMEG (Y) > EMEG (X)\)。

利用梯度幅度相似度偏差(\(GMSD\))度量[26]来测量原始图像和增强图像的感知相似度。 \(GMSD\)是一种全参考的图像质量评价方法，利用像素方向的梯度幅值相似度来捕获图像局部质量，计算总体梯度幅值相似度图的标准差作为最终的图像质量指标。\(GMSD\)是一种简单而有效的方法，它优于目前最先进的全参考图像质量评估方法[26]。\(GMSD\)值越低，原始图像与增强图像之间的失真越小。理想情况下，\(GMSD\)值在原始(\(X\))和增强之间 (\(Y\)) 期望 \(GMSD (X,Y)≈0\)。

B. 定性评估

首先，对灰度图像进行定性评价。第一个测试图像是 \(Order \space in \space Chaos\) [21]中的有序，不同算法的对比度增强结果如图3所示。 这张照片显示的是在中部的格伦沃斯山谷，马匹正通过一条小溪集合海岸，新南威尔士州，澳大利亚[21]。输入图像具有足够高的对比度，并且输入图像的灰度级覆盖了整个动态范围。 因此，对比度增强幅度不大。人们期望，在这种情况下，对比度增强算法应该能够提供最小的变化量的输入，因为感知的对比度足够高。 从结果可以看出，几乎所有的算法都实现了这一点。然而，人们也可以注意到，有一个轻微的过度增强的图像的结果AGCWD和轻微的欠增强是由GHE和EHS引起的。由于GHE有轻微的欠增强，LTHM也有轻微的欠增强。主要是由输入直方图在灰度级“0”处的峰值引起的，该峰值使GHE的输出直方图向右移动，从而产生峰值出现在AGCWD直方图的最右侧。同时，其他算法的输出直方图也有轻微的偏移，在SECE和SECEDCT的输出图像上偏移最小。

第二个测试图像是饿鹅图像[22]，不同算法的对比增强结果如图4所示。 从输入图像的直方图中可以看出，图像的灰度是在中距离处积累的，图像具有对比度改进的余地。GHE和EHS算法实现对比度增强，然而，这伴随着输出图像上较暗外观的视觉假象。 这主要是由于输入图像的直方图主要集中在动态范围的中间值附近，而向中间值的较低方向发展的趋势较大，从而导致图像的某些区域的暗化和过度增强。这是GHE和EHS的一般行为。的直方图加权缓解了的过增强效果从WTHE的结果中可以看出GHE和EHS，HMF, CVC和2DHE。这四种算法提高了输入图像的对比度，几乎与输出图像及其相应的直方图的对比度相同。 虽然与WTHE AGCWD提供了类似的结果,羟甲基糠醛,CVC和2她,不能在使用的整个动态范围,因为原因,用于输入的加权函数直方图极限输出的动态范围图像输入图像的灰度值的最大值,也就是236这个特殊的形象。

由于这个原因，它的对比度增强不够强WTHE, HMF, CVC和2DHE。LTHM降低了由GHE引起的视觉变形水平，增加了局部对比度。然而，由于河引起的严重变形，LTHM也会在一些地区产生具有明显的暗化效果。 LTHS产生稍好一些的结果，因为它将整个变换系数向右平移，这将导致在局部对比度增强的基础上，平均强度的改善。同时，SECE提供了对比度增强，利用整个动态范围，没有任何视觉干扰。 输入直方图的形状在输出直方图中得到体现，这意味着输出图像相对于输入图像具有最小程度的失真。SECEDCT在提供更高的局部对比度增强和全局对比度增强方面进一步提高了SECE算法的性能。此外，SECEDCT利用了整个动态范围，从而获得了更高的对比度。SECE和SECEDCT在输出图像上都提供了没有任何视觉干扰的结果。

第三幅白色Ibis Flip[23]图像如图5所示，并结合不同算法的对比度增强结果。图中，一只白色的朱鹭沿着耶苏普湖的海岸线，用嘴叼着一只小龙虾。从输入图像的直方图可以看出，图像主要由高灰度组成。大多数像素值是在灰度级240附近累积的。 与饥饿的鹅图像一样，这也是全局对比度增强方法的一个难点。从图中可以看出，GHE和EHS的视觉表现最差，HMF和WTHE紧随其后。该算法对输入图像直方图进行加权和阈值化处理，提高了图像质量。然而，仍然可以观察到轻微的变黑效果。 由于CVC和2DHE使用的是加权的灰阶共现，它们能够产生令人满意的结果。LTHM能够减轻GHE的视觉伪影，并且LTHM也能够产生令人满意的结果。这两种算法都能对图像进行全局和局部对比度增强。SECE能够在没有视觉伪影的情况下产生对比度增强的图像。 从SECE输出图像的直方图可以看出，SECE能够将灰度分布在动态范围内，而输入图像的直方图形状并没有明显的变化。SECEDCT也能产生输出，没有明显的视觉伪影，但改善了局部对比度。

图片Portret Krowy[24]是来自波兰的风景，如图6所示。从输入图像的直方图可以看出，大部分的灰度分布是相当均匀的。 算法实现对比度增强而不需要显著的视觉伪影。 这些结果与以往的结果表明，这主要是由于当输入图像的灰度分布相当均匀时，算法的过程变为线性过程，使得输入图像的灰度与处理后的输出图像之间产生一一对应。 一对一的映射有助于在没有重要的可视化工件的情况下生成输出。然而，这并不是SECE和SECEDCT算法在没有明显视觉干扰的情况下产生输出的必要条件。对于输入图像上不同类型的灰度分布，它们通常产生的输出图像没有明显的视觉伪影。

图7所示的波士顿[25]彩色图像的全局对比度衰减级别为“level 1”的结果表明，所有算法都实现了对输入图像的对比度增强。 然而，我们可以看到他和EHS结果的变暗效应。同时，简单地对输入直方图进行加权的算法产生的输出除了AGCWD之外没有任何视觉扭曲。AGCWD不能简单地使用整个动态范围，因为映射函数将输出灰度的最大值映射为输入灰度的最大值233。 CVC和2DHE能够通过增强的输出图像产生令人满意的输出图像。这主要是由于像素的灰度共生点均匀分布在输入图像上。变换域meth- ods LTHM和LTHS在输入图像的对比度水平上提供了显著的改进。 与此同时, SECE 生成的输出图像没有任何明显的视觉失真，其直方图与输入直方图形状的相似性最大。SECEDCT进一步提高了局部对比度。

进一步的“级别2”和“级别3”的全局对比度衰减级别的图像分别显示在图8和图9[25]中。 从图中可以看出，所有的算法都实现了对比度增强。然而，在低对比度图像上，AGCWD的对比度增强水平始终低于其他算法。 这是由于在映射函数中使用了裁剪值。同时，在不考虑图像灰度分布类型的情况下，利用SECE算法实现全局对比度增强。 这表明使用空间位置而不是直接的灰度级可以实现无伪影的对比度增强。此外，SECEDCT还实现了与SECE类似的无伪影增强，进一步提高了局部对比度。

C. 对比度增量的定量检测

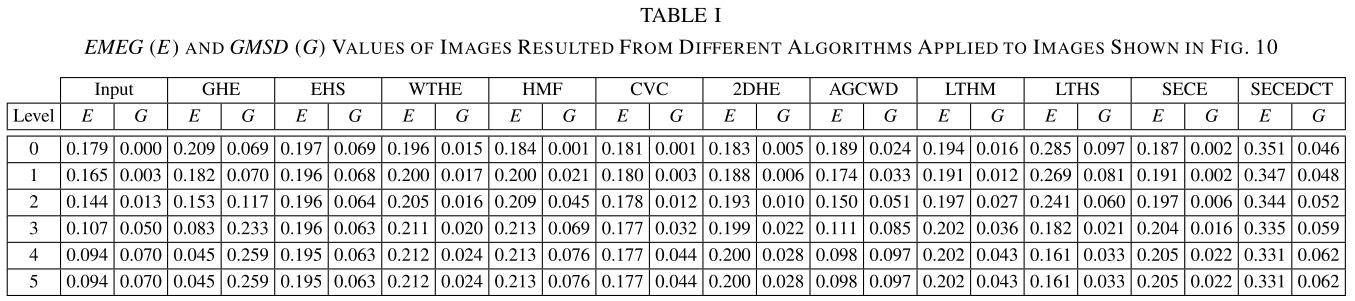
在本节中，我们使用了来自 \(CSIQ\) 图像数据库[25]的全局对比度衰减程度不同的图像，来评估不同算法在视觉失真能力最小的情况下对比度的改善情况 。对于每个算法的结果，测量相应的 \(EMEG\) 和 \(GMSD\) 值，定量评估对比度增强和图像失真的程度。测试的结果和相应的测量在图10和表1中， \(GMSD\) 值在无失真的原始图像(“0级”)和经过处理或全局对比度衰减的图像之间进行测量。

在“3级”之后，由于全局对比度降低而出现明显的失真。在此之前，所有的算法都能够在没有明显视觉扭曲的情况下改善对比度。这也可以从测量的水平上看出 \(GMSD\)。然而，对比增强对 \(AGCWD\) 的结果影响最小。在“3级”之后，\(GHE\) 产生的结果是不能接受的。只对 \(SECE\) 和在 \(SECEDCT\) 中，原始图像和增强图像的对比度改善和失真水平在不同程度的衰减后几乎保持不变。这表明，这两种算法能够对具有不同对比度衰减程度的图像进行相似程度的对比度增强。

D. 定量评定

为了评估对比度增强算法对广泛范围图像的性能，将其应用于500张伯克利图像数据集[20]的作为测试图像。 在原始图像和增强图像之间计算 \(EMEG\) 和 \(GMSD\) 测量值，以创建测量值集合。 该集合计算使用所有增强图像 \(\{Y_i\}_{∀}\) 和相对应的原始图像 \(\{X_i\}_{∀}\) 统计决定对比度增强算法是否符合期望的测量指标。 每个准则提出两个假设: 原假设\(H0\) 和替代假设 \(H1\) 。非参数双样本Kolmogorov-Smirnov检验(KS-test)[27]用于拒绝其中一个假设。KS-test试图通过分配一个 \(p\) 值来量化两个数据集之间的逻辑关系\((=，>，<)\)，它的优点是不需要对数据的分布做任何假设。 \(p\) 值表示得到测试统计量的概率至少与零假设[27]下观察到的概率一样极端。 因此，\(p\) 值越高，零假设越强。\(p\) 值与\(%95\) 的显著性水平一起使用时，如果 \(p< 0.05\), \(H_0\) 被拒绝，取而代之的是 \(H1\)。

为了检验算法相对于其他算法的相对对比度改进，我们使用双样本KS-test来检验以下假设:

\[H 0 : A \space produces \space higher \space contrast \space wrt\space B; \\ H 1 : A \space does \space not \space produce \space higher \space contrast \space wrt \space B, \space (15) \]

其中，原假设H 0提出算法A产生的对比度比算法B高， \(\{EMEG(Y_i^{A})>EMEG(Y_i^{B})\}_{∀}\) ，在 \(Y_i^A\) 和 \(Y_i^B\) 分别是由算法 \(A\) 和算法 \(B\) 在输入图像 \(Xi\) 下的输出图像。 得到的 \(p\) 值如表2所示，其中Input指的是没有任何处理的原始图像。

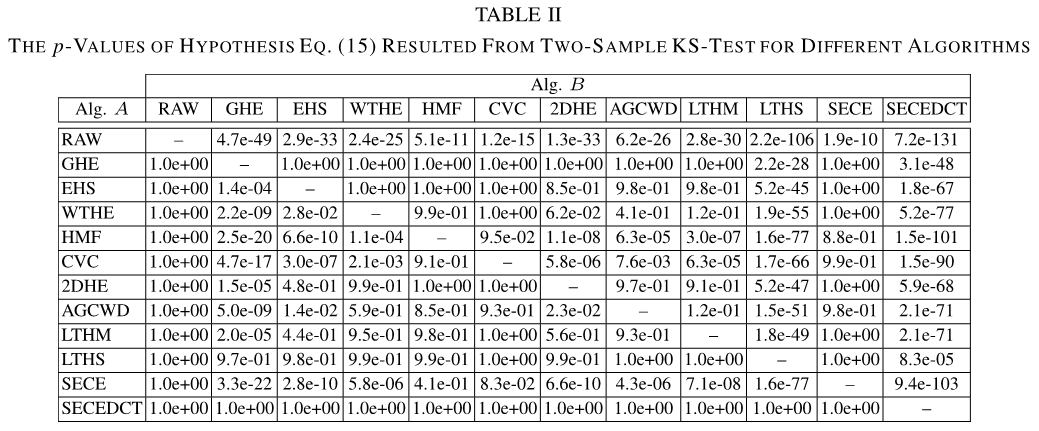
在输入图像有改进余地的情况下，期望对比度增强算法能提高输入图像的对比度。 因此，至少可以预测增强后图像的 \(EMEG\) 要高于原始图像的 \(EMEG\)。式(15)中原假设的结果 \(p\) 值如表2的第一行所示。 根据95%的置信水平，所有的算法都拒绝 \(H0\)，即原始图像的对比度低于不同算法的增强图像的对比度。因此，统计上所有的算法都产生了比原始图像对比度更高的图像。

从表II中还可以清楚地看出，SECEDCT能提供最高的对比度增强，其次是LTHS、GHE、EHS和LTHM。这是转换域算法的预期结果SECEDCT和LTHS可以同时进行全局增强和局部增强。并对其性能进行了分析紧随LTHS之后的是GHE和EHS的性能，这两种方法的运行方式几乎相同，即使结果不相同，但结果相似。 由于LTHM是为了减少GHE的视觉伪影而设计的，所以它的输出对比度比预期的GHE要低。SECEDCT，LTHS，EHS和LTHM在输出图像对比度方面优于其他算法。然而，正如在定性分析中所看到的，这并不总是意味着它们总是提供视觉上令人愉悦的结果。 SECEDCT算法是个例外。加工后的外观观察500幅图像显示，SECEDCT提高了输入图像的对比度，但没有在输出图像上产生明显的视觉伪影，而LTHS，GHE, EHS 和 LTHM并不总是这样。 2DHE遵循SECEDCT，LTHS，GHE，EHS 和 LTHM。其次是HMF、WTHE、CVC、SECE和AGCWD。AGCWD提供最低水平的对比度增强。 AGCWD提供最低水平的对比度增强 。

然而，\(EMEG\) 的高水平并不一定意味着产生的输出图像没有失真。为了检验不同对比度增强方法对图像造成的失真，我们使用原始( \(X\) )和增强( \(Y\) )之间的 \(GMSD\) 值 \(GMSD (X,Y)\) 作为检验统计量，使用双样本KS-test对不同算法进行以下假设检验 :

\[H 0 : A \space produces\space less\space distortion\space wrt\space B; \\ H 1 : A\space does\space not\space produce\space less\space distortion\space wrt\space B, \space (16) \]

在原假设 \(H0\) 中，算法 \(A\) 生成的输出图像的失真比算法 \(B\) 的要小，\(\left\{G M S D\left(\mathbf{X}_{i}, \mathbf{Y}_{i}^{A}\right)<G M S D\left(\mathbf{X}_{i}, \mathbf{Y}_{i}^{B}\right)\right\}_{\vee i}\) ，其中 \(Y_i^A\) 和 \(Y_i^B\) 分别是算法 \(A\) 和算法 \(B\) 的输出图像。 得到的 \(p\) 值如表3所示。有趣的是，SECEDCT提供了与所有算法相比更高的对比度， 与GHE相比，输出图像的失真更小，
EHS, WTHE, 2DHE, AGCW, LTHM, LTHS。同时，最小失真由SECE提供。

表2和表3的结果表明，虽然SECE算法提高了输入图像的对比度，但与其他算法相比，它对输出图像产生的视觉失真最小。

E. 对比度增强对目标识别的影响

对比度增强常被用作基于外观的物体识别的预处理。然而，对比度增强算法的性能会影响目标识别过程。 为验证效果，选取人脸为对象，对CMU PIE数据库[28]对比度增强后的C27正面图像进行人脸识别。人脸识别任务实现如下:对于数据库中的每个受试者，将存储一组训练图像(本例中为25张)。 训练数据库由一组特征向量表示，这些特征向量是用2DPCA计算得到的。每个训练图像被投影到特征向量上，并为每个受试者存储一组投影向量。根据其投影向量与数据库中被试投影向量之间的最小欧氏距离来识别查询面。特征向量的数量决定了人脸识别率。

CMU PIE额面部(C27)数据库[28]包含68名受试者的图像，每个受试者提供49张不同光照和表情条件下的额面部图像。所有图像均为灰度，归一化为64×64像素分辨率。 对于数据库中的每个受试者，使用25张图像进行培训，其余24张图像用于查询(测试)图像。因此，训练样本总数为1700个，测试样本总数为1632个。表4的识别结果表明，SECE增强图像的人脸识别效果最好，其次是SECEDCT增强图像。 这表明SECE保留了图像的整体内容。有趣的是，在大多数应用中，GHE都被用作大多数图像处理/计算机视觉应用的预处理算法。然而，它大大降低了图像的外观，导致性能损失，这通常是被忽视的。

F. SECEDCT对比度增强的程度

SECEDCT是SECE的一个泛化版本，并且SECEDCT与的输出完全相同为 $ \gamma= 0 $ 时被选中。$ \gamma $ 的值的增加也会增加的水平的局部对比度增强方法，反之亦然。尽管可以设置为$ \gamma=0.5 $ 作为默认值，可以进一步通过 \(\gamma\) 的值改变感知局部对比度的水平。

为了证明，定性和定量结果不同的 $ \gamma $ 值图11所示。 结果表明，$ \gamma $ 的值的增加也会增加局部对比度的水平，\(EMEG\) 方法也是如此。局部对比度的增加会导致局部像素统计的变化。这将反映在原始(输入)和处理后的图像之间的\(GMSD\) 值上。 从测量结果可以看出，局部对比度增强程度越高，\(GMSD\) 值越高。然而，还可以注意到，即使在高水平的局部对比度增强方法实现 $ \gamma $ 的值高，视觉效果也没有表现出显著的扭曲。

G. 计算时间

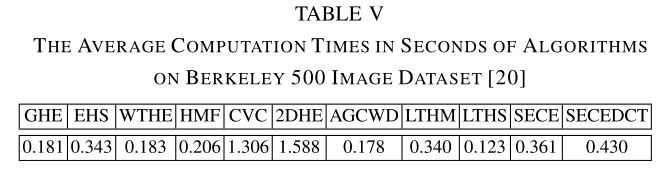
算法的计算时间要求是一个重要的因素。在本节中，我们提供了不同对比度增强算法对Berkeley 500图像数据集[20]的平均处理时间，该数据集由大小为321×481或481×321的图像组成。所有算法在MATLAB R2013a中实现。测试是在一台运行12.0GB RAM和Intel(R) Core(TM) i5-3317U 1.70GHz CPU的64位Windows 7笔记本电脑上进行的。表5结果表明，与其他算法相比，LTHS的计算时间最短。这主要是由于LTHS只计算图像的2D-DCT，移动变换域系数的直方图，然后再取倒数2维变换。该算法能有效地计算二维- dct变换及其反变换，变换域直方图的移位简单易行。

5. 结论

在本文中，我们提出了一种计算效率高的全局对比度增强算法SECE，该算法利用输入图像的灰度空间位置分布来进行非线性数据映射，从而在不同类型的图像上生成自然的增强效果。SECE既可以应用于灰度图像，也可以应用于彩色图像，并且不需要设置参数。根据实验数据分析，该方法在提高图像对比度的同时，对输出图像几乎不产生视觉失真。SECE保留了输入图像的灰度直方图，同时提高了对比度。这主要是因为SECE利用像素的空间位置信息，并据此找到一个非线性的映射。由于保留了输入直方图的形状，这对于一些需要进行预处理的应用(如人脸识别)来说是至关重要的，因此SECE可以应用于这样的需求。实验结果还表明，SECE增强后的人脸识别结果比其他增强算法增强后的结果更好。

为了同时实现全局对比度增强和局部对比度增强而不产生视觉失真，提出了一种变换域算法SECEDCT。SECEDCT扩展了SECE，同时进行全局和局部对比增强。SECEDCT自动更新经过SECE增强的图像的变换域系数。 它是SECE算法的一个广义版本，由一个改变感知局部对比度的参数控制。将此参数设置为0，则SECEDCT变为SECE，在给定范围内增加参数值，可提高图像的局部对比度。

参考文献

[1] R. C. Gonzalez and R. E. Woods, Digital Image Processing, 3rd ed. Upper Saddle River, NJ, USA: Prentice-Hall, 2006.
[2] T. Celik, “Two-dimensional histogram equalization and contrast enhancement,” Pattern Recognit., vol. 45, no. 10, pp. 3810–3824, 2012.
[3] D. J. Jobson, Z.-U. Rahman, and G. A. Woodell, “A multiscale retinex for bridging the gap between color images and the human observation of scenes,” IEEE Trans. Image Process., vol. 6, no. 7, pp. 965–976, Jul. 1997.
[4] B. Silver, S. Agaian, and K. Panetta, “Contrast entropy based image enhancement and logarithmic transform coefficient histogram shifting,” in Proc. IEEE Int. Conf. Acoust., Speech Signal Process., vol. 2. Mar. 2005, pp. 633–636.
[5] B. Silver, S. Agaian, and K. Panetta, “Logarithmic transform coefficient histogram matching with spatial equalization,” Proc. SPIE, vol. 5817, pp. 237–249, May 2005.
[6] S. S. Agaian, B. Silver, and K. A. Panetta, “Transform coefficient histogram-based image enhancement algorithms using contrast entropy,” IEEE Trans. Image Process., vol. 16, no. 3, pp. 741–758, Mar. 2007.
[7] J. Mukherjee and S. K. Mitra, “Enhancement of color images by scaling the DCT coefficients,” IEEE Trans. Image Process., vol. 17, no. 10, pp. 1783–1794, Oct. 2008.
[8] R. Fattal, “Edge-avoiding wavelets and their applications,” ACM Trans. Graph., vol. 28, no. 3, pp. 1–10, 2009.
[9] T. K. Kim, J. K. Paik, and B. S. Kang, “Contrast enhancement system using spatially adaptive histogram equalization with temporal filtering,” IEEE Trans. Consum. Electron., vol. 44, no. 1, pp. 82–87, Feb. 1998.
[10] E. Wharton, K. Panetta, and S. Agaian, “Human visual system-based image enhancement and logarithmic contrast measure,” Proc. SPIE, vol. 6497, 2007.
[11] E. Wharton, K. Panetta, and S. Agaian, “Human visual system based multi-histogram equalization for non-uniform illumination and shoadow correction,” in Proc. IEEE Int. Conf. Acoust., Speech Signal Process., vol. 1. Apr. 2007, pp. 729–732.
[12] K. Panetta, E. Wharton, and S. Agaian, “Human visual system-based image enhancement and logarithmic contrast measure,” IEEE Trans. Syst., Man, Cybern. B, Cybern., vol. 38, no. 1, pp. 174–188, Feb. 2008.
[13] D. Coltuc, P. Bolon, and J.-M. Chassery, “Exact histogram specification,” IEEE Trans. Image Process., vol. 15, no. 5, pp. 1143–1152, May 2006.
[14] Q. Wang and R. K. Ward, “Fast image/video contrast enhancement based on weighted thresholded histogram equalization,” IEEE Trans. Consum. Electron., vol. 53, no. 2, pp. 757–764, May 2007.
[15] T. Arici, S. Dikbas, and Y. Altunbasak, “A histogram modification framework and its application for image contrast enhancement,” IEEE Trans. Image Process., vol. 18, no. 9, pp. 1921–1935, Sep. 2009.
[16] S.-C. Huang, F.-C. Cheng, and Y.-S. Chiu, “Efficient contrast enhancement using adaptive gamma correction with weighting distribution,” IEEE Trans. Image Process., vol. 22, no. 3, pp. 1032–1041, Mar. 2013.
[17] T. Celik and T. Tjahjadi, “Automatic image equalization and contrast enhancement using Gaussian mixture modeling,” IEEE Trans. Image Process., vol. 21, no. 1, pp. 145–156, Jan. 2012.
[18] T. Celik and T. Tjahjadi, “Contextual and variational contrast enhancement,” IEEE Trans. Image Process., vol. 20, no. 12, pp. 3431–3441, Dec. 2011.
[19] C. Lee, C. Lee, and C.-S. Kim, “Contrast enhancement based on layered difference representation of 2D histograms,” IEEE Trans. Image Process., vol. 22, no. 12, pp. 5372–5384, Dec. 2013.
[20] P. Arbelaez, M. Maire, C. Fowlkes, and J. Malik, “Contour detection and hierarchical image segmentation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 3, no. 5, pp. 898–916, May 2011.
[21] (Feb. 16, 2010). Kodak Moment of the Day. [Online]. Available: http://www.kodak.com
[22] (Jan. 6, 2011). Kodak Moment of the Day. [Online]. Available: http://www.kodak.com
[23] (Aug. 4, 2014). Kodak Moment of the Day. [Online]. Available: http://www.kodak.com
[24] (Jul. 11, 2014). Kodak Moment of the Day. [Online]. Available: http://www.kodak.com
[25] E. C. Larson and D. M. Chandler, “Most apparent distortion: Full-reference image quality assessment and the role of strategy,” J. Electron. Imag., vol. 19, no. 1, pp. 011006-1–011006-21, Mar. 2010.
[26] W. Xue, L. Zhang, X. Mou, and A. C. Bovik, “Gradient magnitude similarity deviation: A highly efficient perceptual image quality index,” IEEE Trans. Image Process., vol. 23, no. 2, pp. 684–695, Feb. 2014.
[27] D. J. Sheskin, Handbook of Parametric and Nonparametric Statistical Procedures, 4th ed. London, U.K.: Chapman & Hall, 2007.
[28] T. Sim, S. Baker, and M. Bsat, “The CMU pose, illumination, and expression database,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 25, no. 12, pp. 1615–1618, Dec. 2003.
[29] J. Yang, D. Zhang, A. F. Frangi, and J.-Y. Yang, “Two-dimensional PCA: A new approach to appearance-based face representation and recognition,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 26, no. 1, pp. 131–137, Jan. 2004.

​