Squeeze-and-Excitation Networks（SENet 2017）

 

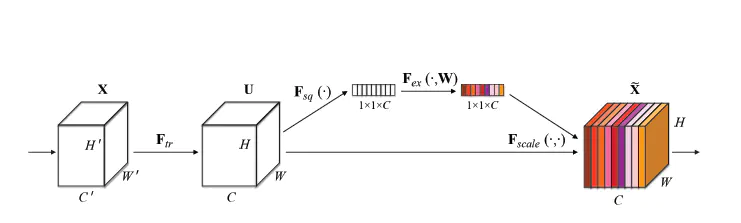
 Figure 1 SE Block

 

Figure 1 是SENet的Block单元，图中的F_tr是传统的卷积结构，X和U是F_tr的输入（C'✖H'✖W'）和输出(C✖H✖W)，这些都是基本的卷积操作。SENet增加的部分是U后的结构：对U先做一个Global Average Pooling（图中的F_sq(.)，作者称为Squeeze过程），输出的1x1xC数据再经过两级全连接（图中的F_ex(.)，作者称为Excitation过程），最后用sigmoid（论文中的self-gating mechanism）限制到[0，1]的范围，把这个值作为scale乘到U的C个通道上， 作为下一级的输入数据。这种结构的原理是想通过控制scale的大小，把重要的特征增强，不重要的特征减弱，从而让提取的特征指向性更强。 

SE block的最后输出为 1x1xC 的通道加权向量。 因为卷积运算 隐式 地包含了通道加权操作，所以为什么要显示地给每个channel学习一个权重呢？ 因为训练完成后，conv的隐式加权的权重是 固定 的， 而 SE 输出的权重向量是 data independent的， 是随着输入数据动态变化的。所以明确：attention机制的一大特点： 动态。此外， SE模块和传统的卷积间采用并联而不是串联的方式， 这是因为SE利用的是U的相关性来计算scale，X和U的相关性是不同的，把根据X的相关性计算出的scale应用到U上明显不合适 (动态调整）。

def Squeeze_excitation_layer(self, input_x, out_dim, ratio, layer_name):
    with tf.name_scope(layer_name) :
        squeeze = Global_Average_Pooling(input_x) #Squeeze, 全局平均池化

　　　　 # Excitation， 采用两个全连接网络进行信息的综合
        excitation = Fully_connected(squeeze, units=out_dim / ratio, layer_name=layer_name+'_fully_connected1')
        excitation = Relu(excitation)
        excitation = Fully_connected(excitation, units=out_dim, layer_name=layer_name+'_fully_connected2')
        excitation = Sigmoid(excitation) # scale  信息的归一化处理  [0, 1]
        excitation = tf.reshape(excitation, [-1,1,1,out_dim])
        scale = input_x * excitation
        return scale


def Fully_connected(x, units=class_num, layer_name='fully_connected'):with tf.name_scope(layer_name) :
　　 with tf.name_scope(layer_name) :
　　　　return tf.layers.dense(inputs=x, use_bias=False, units=units) 

Squeeze （全局信息整合， Global Information Embedding）

为了解决利用通道之间的依赖关系的问题，作者首先考虑了在输出特征组图中各个通道的信号本身。在卷积操作中，每个卷积核只作用于自身感受野，这导致其无法利用感受野之外的上下问信息。为了缓解这个问题，作者提出squeeze 操作来提取全局空间特征信息。作者用了最简单的求平均的方法（全局平局池化，Global Average Pooling），将空间上所有点的信息都平均成了一个值。这么做是因为最终的scale是对整个通道作用的，这就得基于通道的整体信息来计算scale。另外作者要利用的是通道间的相关性，而不是空间分布中的相关性，用GAP屏蔽掉空间上的分布信息能让scale的计算更加准确。

 

 

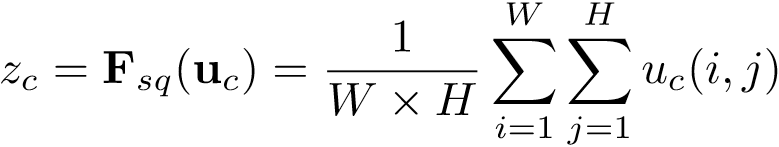
Excitation (自适应校准，Adaptive Recalibration）

在文中作者提到Excitation 必须具备两个特征：1）具有灵活性（特别是要能够学习通道之间的非线性交互）；2）必须能学习。为了满足这些标准，作者使用了一种具有Sigmoid激活的简单门机制进行操作，对数据的具体运算如下式所示。

 

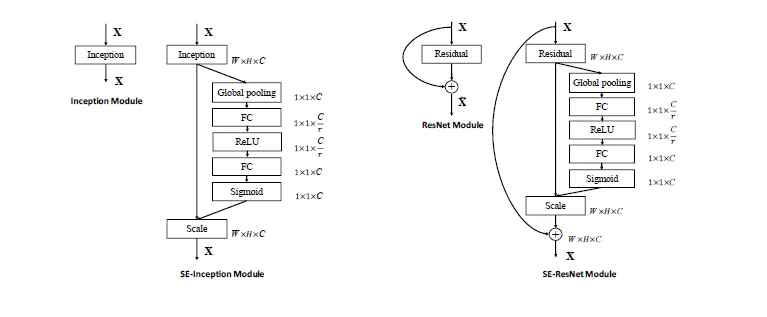
   Figure 2 SE-Inception和SE-ResNet结构

Excitation部分中第一个全连接把C个通道压缩成了C/r个通道来降低计算量（后面跟了RELU），第二个全连接再恢复回C个通道（后面跟了Sigmoid），r是指压缩的比例。作者尝试了r在各种取值下的性能 ，最后得出结论r=16时整体性能和计算量最平衡。为什么要加全连接层呢？这是为了利用通道间的相关性来训练出真正的scale。一次mini-batch个样本的squeeze输出并不代表通道真实要调整的scale值，真实的scale要基于全部数据集来训练得出，而不是基于单个batch，所以后面要加个全连接层来进行训练。

论文: https://arxiv.org/abs/1709.01507

tensorflow:https://github.com/taki0112/SENet-Tensorflow

 参考博客：

【1】https://zhuanlan.zhihu.com/p/29812913

【2】https://blog.csdn.net/u011961856/article/details/77924041

【3】https://blog.csdn.net/u014380165/article/details/78006626

【4】https://www.jianshu.com/p/59fdc448a33f

【5】https://www.jianshu.com/p/80777e7abb8a

【6】https://blog.csdn.net/yuzhijiedingzhe/article/details/78124752