图的基本概念与常用算法

图

图的基本定义

（学艺不精，图画的不好，望见谅）

图的定义

1.图的定义

无论多么复杂的图，都是由顶点和边构成的。图G由两个集合V和E组成，记成G=（V,E），其中V是顶点的有限集合，E是连接V中两个不同顶点（顶点对）的边的有限集合，记成E（G）。

2.有向图

定义：如果表示边的顶点对（或序偶）是有序的，则称G为有向图。

ps:在有向图中表示边的顶点对用尖括号括起来，用于表示一条有向边，如表示从顶点i到顶点j的一条边，可见<i,j>和<j,i>是两条不同的边 。

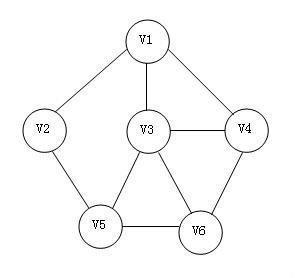
3.无向图

定义：如果在图G中，若<i,j>∈E(G)必有<j,i>∈E(G),即E(G)是对称的，则用（i,j)代替这两个顶点对,表示顶点i与顶点j的一条无向边，则称G为无向图。

4.图的抽象数据类型定义

ADT Graph

{数据对象:
D={ai|1≤i<=n,n>=0,ai为ElemType类型} //ElemType是自定义类型标识符
数据关系:
R= {<ai,aj>|ai、aj∈D,1<=i,j<=n,其中每个元素可以有零个或多个前装元素，可以有零个或多个后继元素}
基本运算:
CreateGraph( &g):创建图，由相关数据构造一个图g。

     DestroyGraph(&g):销毁图，释放图g占用的存储空间。

     DispGraph(g):输出图，显示图g的顶点和边信息。

     DFS(g,v):从顶点v出发深度优先遍历图g。

     BFS(g,v):从顶点v出发广度优先遍历图g。

图的基本术语

1.端点和邻接点

在一个无向图中,若存在一条边(i,j)，则称顶点 i和顶点j为该边的两个端点,并称它们互为邻接点,即顶点i是顶点j的一个邻接点，顶点i也是顶点j的一个邻接点，边(i,j)和顶点i、j关联。关联于相同两个端点的两条或者两条以上的边称为多重边，在数据结构中讨论的图都是指没有多重边的图。

在一个有向图中,若存在一条有向边<i,j>(也称为弧)，则称此边是顶点i的一条出边,同时也是顶点j的一条入边,i为此边的起始端点(简称为起点)，j为此边的终止端点(简称终点),顶点j是顶点i的出边邻接点,顶点i是顶点j的入边邻接点。

2.顶点的度、入度和出度

在无向图中，一个顶点所关联的边的数目称为该顶点的度。在有向图中,顶点的度又分为人度和出度，以顶点j为终点的边数目,称为该顶点的入度。以顶点i为点的边数目,称为该顶点的出度。一个顶点的入度与出度的和为该顶点的度。
(ps:一个图中，所有顶点的度之和等于边数的两倍。）

3.完全图

若无相图中的每两个顶点之间都存在着一条边，有向图中的每两个顶点之间都存在着方向相反的两条边，则称此图为完全图。

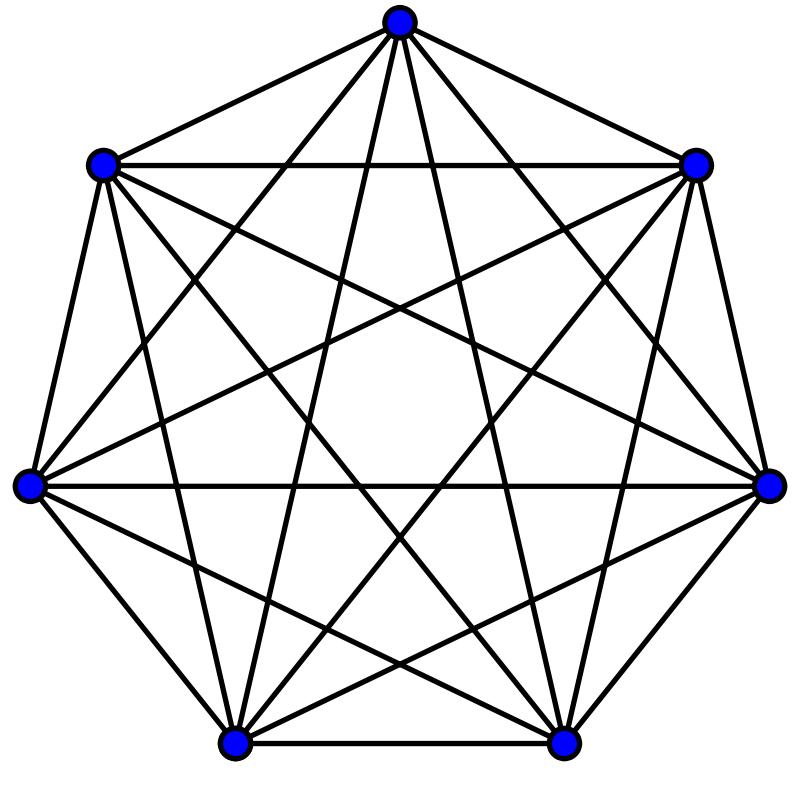
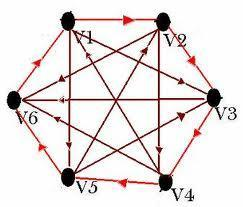
有向完全图：有向图中的每两个顶点之间都存在着方向相反的两条边。

ps:有向完全图包含n(n-1)条边。

无向完全图：每两个顶点之间都存在一条边。

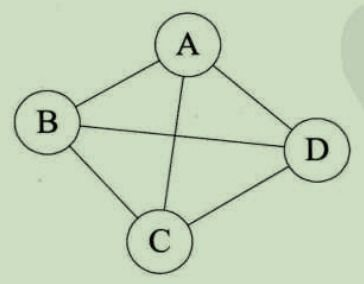
ps:有向完全图包含n(n-1)/2条边。

4.稠密图和稀疏图

稠密图：当一个图接近完全图时。

稀疏图：当一个图含有较少的边数时。

5.子图

6.路径和路径长度

7.回路或环

若一条路径上的开始点与结束点为同一个顶点，则此路径被称为回路或环。开始点与结束点相同的简单路经被称为简单回路或简单环。

8.连通、连通图和连通分量

在无向图G中，若从顶点i到顶点j有路径,则称顶点i和顶点j是连通的。若图G中的任意两个顶点都是连通的则称G为连通图,否则称为非连通图。无向图G中的极大连通子图称为G的连通分量，显然连通图的连通分量只有一个（即本身）而非连通图有多个连通分量。

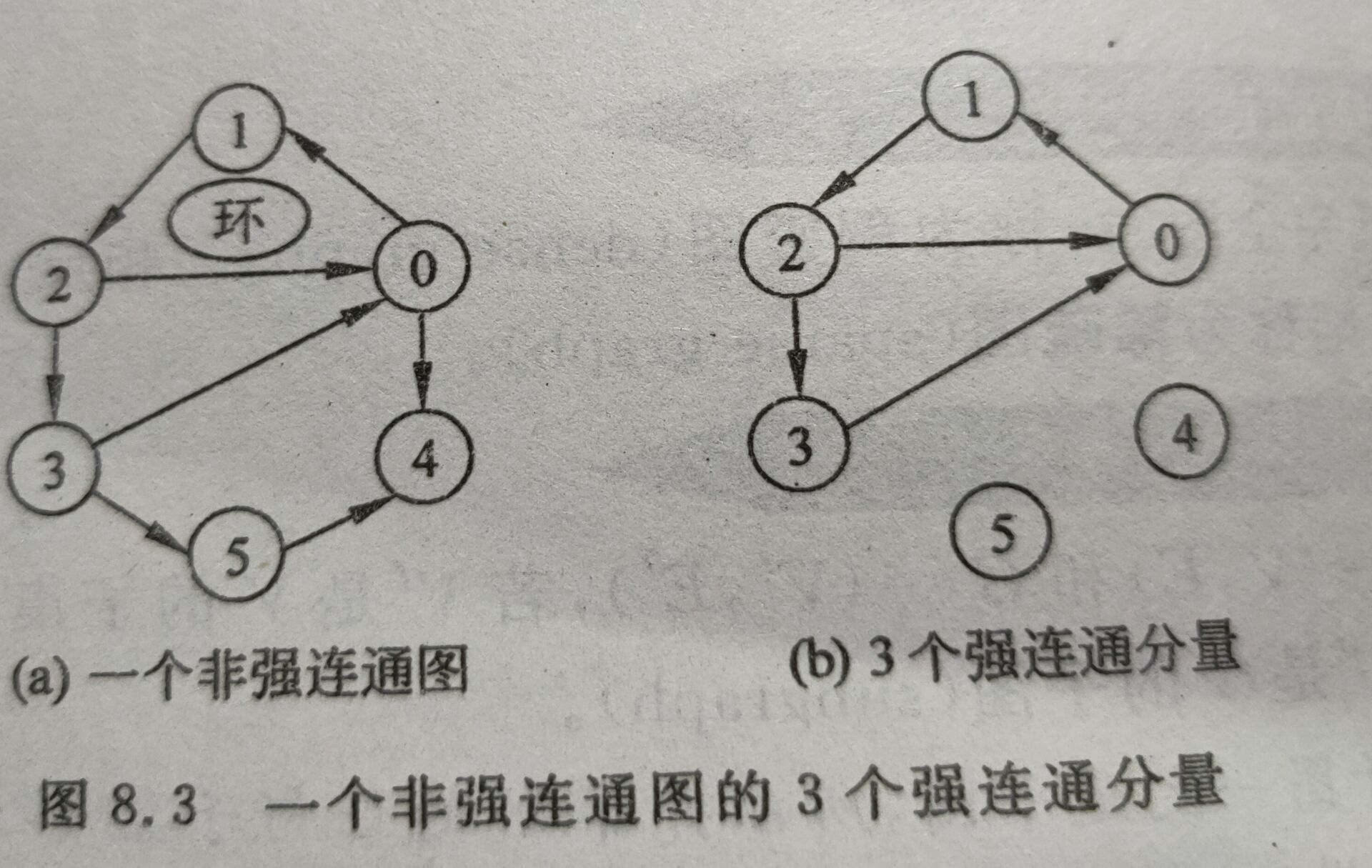
9.强连通图和强连通分量

在有向图G中，若从顶点i到顶点j有路径,则称从顶点i到顶点j是连通的，若图G中的任意两个顶点i和j都连通，即从顶点i到顶点j和从顶点j到顶点i都存在路径则称途径是强连通图。

ps:强连通图只有一个强连通分量（即它本身）。

在一个非常连通图中找强连通分量的方法如下 ：

（1）在图中找有向环。

（2）拓展该有向环：如果某个顶点到该环中的任何一项顶点都有路径，并且该环中的任一顶点到这个顶点也有路径，则加入这个顶点。

10.权和网

图中的每一条边都可以附有一个对应的数值，这种与边相关的数值称为权，权可以表示从一个顶点到另一个顶点的距离或花费的代价，边上带有权的图称为带权图，也称为网。

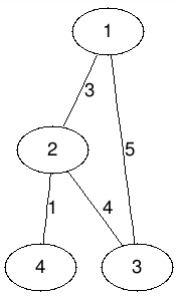
带权无向图

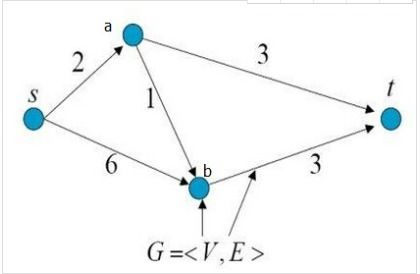
带权有向图

图的存储结构和基本运算算法

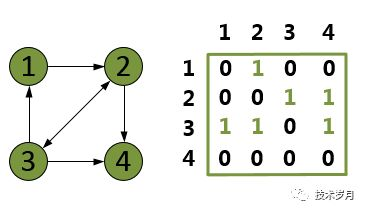
邻接矩阵存储方法

在邻接矩阵中判断图中，两个顶点之间是否有边或者求两个顶点之间边的权的执行时间为O(1)，所以在需要提取边权值的算法中，通常采用邻接矩阵存储结构。

邻接表存储方法

图的邻接表是一种顺序链式存储相结合的存储方法。

在邻接表中有两种类型的结点，一种是头结点，其个数恰好为图中顶点的个数，另一种是边结点，也就是单链表中的结点。对无向图，这类结点的个数等于边数的两倍；对有向图，这类结点的个数等于边数。

邻接表结构体：
typedef struct ANode //边结点； { int adjvex;//指向该边的终点编号； struct ANode*nextarc;//指向下一个邻接点； INfoType info;//保存该边的权值等信息； }ArcNode; typedef struct //头结点 { int data;//顶点； ArcNode *firstarc;//指向第一个邻接点； }VNode; typedef struct { VNode adjlist[MAX];//邻接表； int n,e;//图中顶点数n和边数e； }AdjGraph;

可以看出，对于边数目较少的稀疏图，邻接表比邻接矩阵更节省存储空间。

图的遍历

图的遍历的概念

从给定图中任意指定的顶点（称为初始点）出发，按照某种搜索方法沿着图的边访问图中的所有顶点，使每个顶点仅被访问一次，这个过程称为图的遍历。
按照搜索方法的不同，图的遍历方法有两种，一种是深度优先遍历（DFS),另一种叫广度优先遍历(BFS)。

深度优先遍历

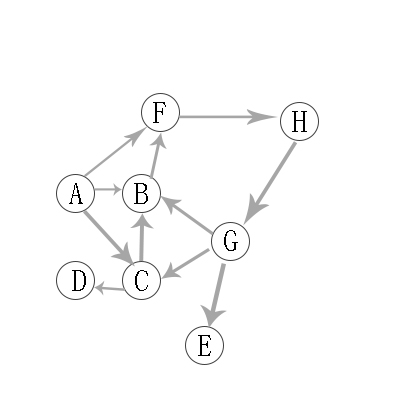
深度优先遍历的过程是从图中的某个初始点v出发,首先访问初始点v,然后选择一个与顶点为相邻且没被访问过的顶点w,以w为初始顶点，再从它出发进行深度优先遍历 直到图中与顶点为邻接的所有顶点都被访问过为止。容易看出，这是一个递归过程。

如：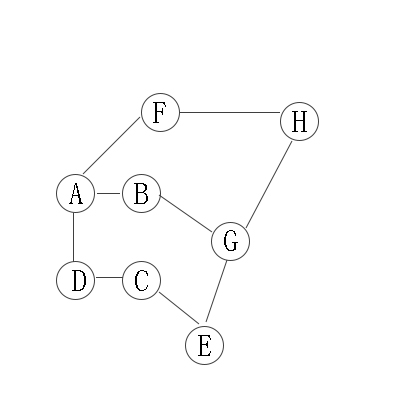
遍历结果为A -> B -> G -> E -> C -> D -> H -> F

深度优先算法：
int vsited[MAX]= {0}; //全局数组
void DFS(AdjGraph * G,int v) //深度优先遍历算法
{ArcNode * p;
visited[v]=1; //置已访向标记
printf("%d",v); //输出被访向顶点的编号
p=G一adjlist[v]. firstarc; //p指向顶点v的第一个邻接点
while (p!= NULL){
if (visited[p-> adjvex]==0) //若p->adivex顶点未被访问，递归访问它
DFS(G,p-> adjvex);
p于P->nextarc; //p指向顶点v的下一一个邻接点
}

广度优先遍历

广度优先遍历是连通图的一种遍历策略。从图中某个顶点V0出发，并访问此顶点，然后从V0出发，访问V0的各个未曾访问的邻接点W1，W2，…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点，再重复上一步骤，直到全部顶点都被访问为止。这也是一个递归过程。

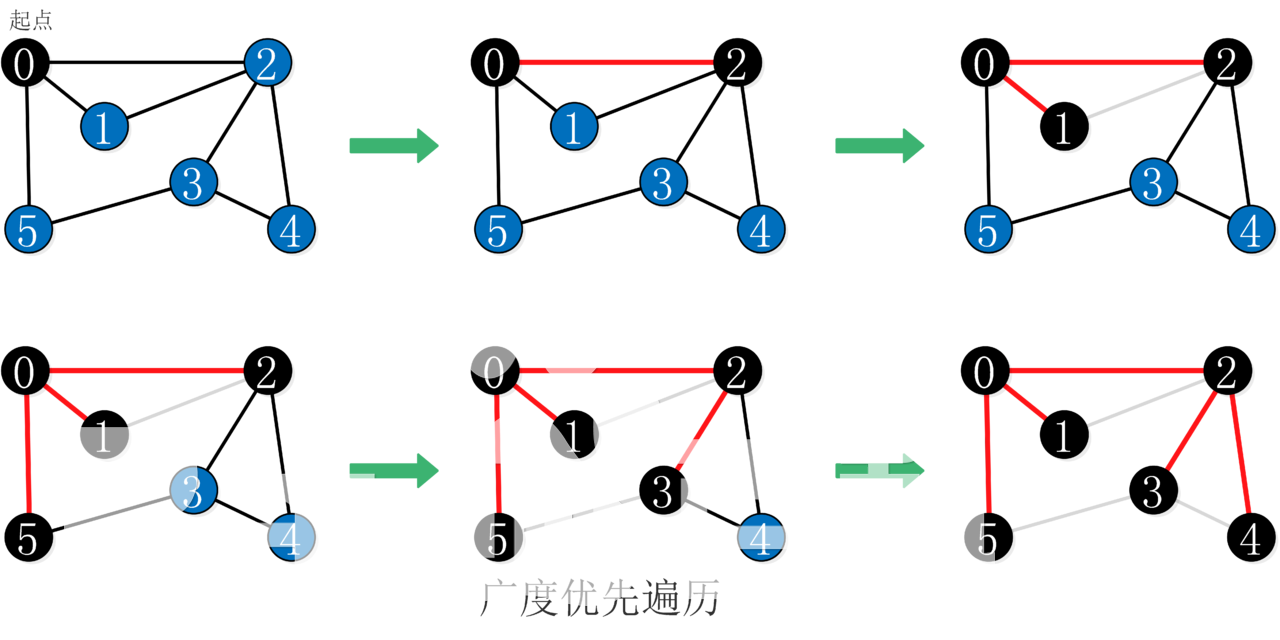
例如如下图，广度优先遍历得到的答案是A -> B -> C -> F -> D -> H -> E -> G

生成树和最小生成树

按照生成树的定义,n个顶点的连通图的生成树有n个顶点、(n-1)条边。因此，构造最小生成树的准则有以下3条:

(1)必须只使用该图中的边来构造最小生成树;

(2)必须使用且仅使用(n- 1)条边来连接图中的n个顶点;

(3)不能使用产生回路的边。

ps:求图的最小生成树的两个算法：普里姆算法、克鲁斯卡尔算法。

无向图

深度优先树和广度优先树

由深度优先遍历得到的生成树称为深度优先生成树。在深度优先遍历中，如果将每次“前进”(纵向)路过的(将被访问)顶点和边都记录下来,就得到了一个子图，该子图为以出发点为根的树，就是深度优先生成树。

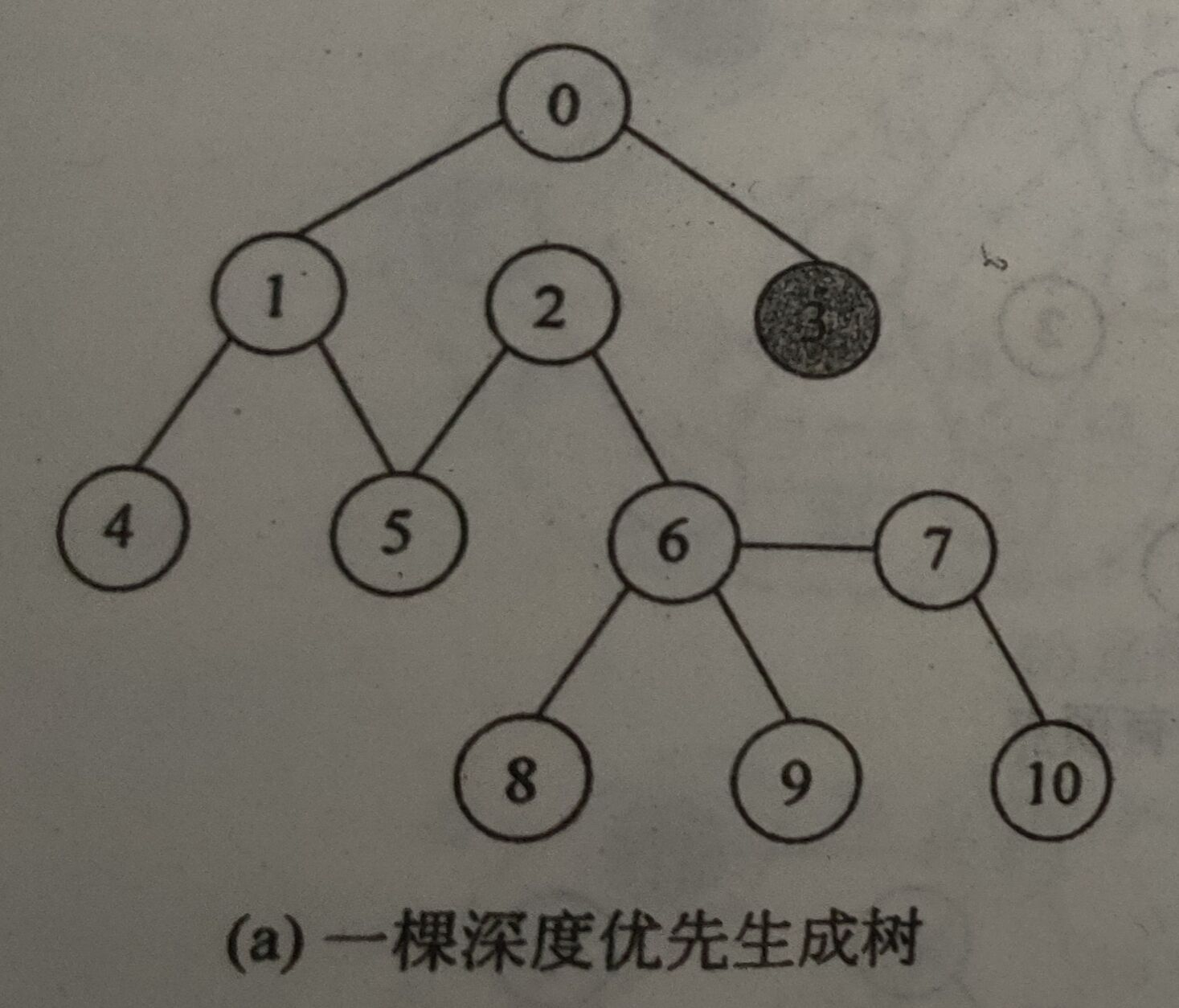
深度优先树

相应地，由广度优先遍历得到的生成树称为广度优先生成树。

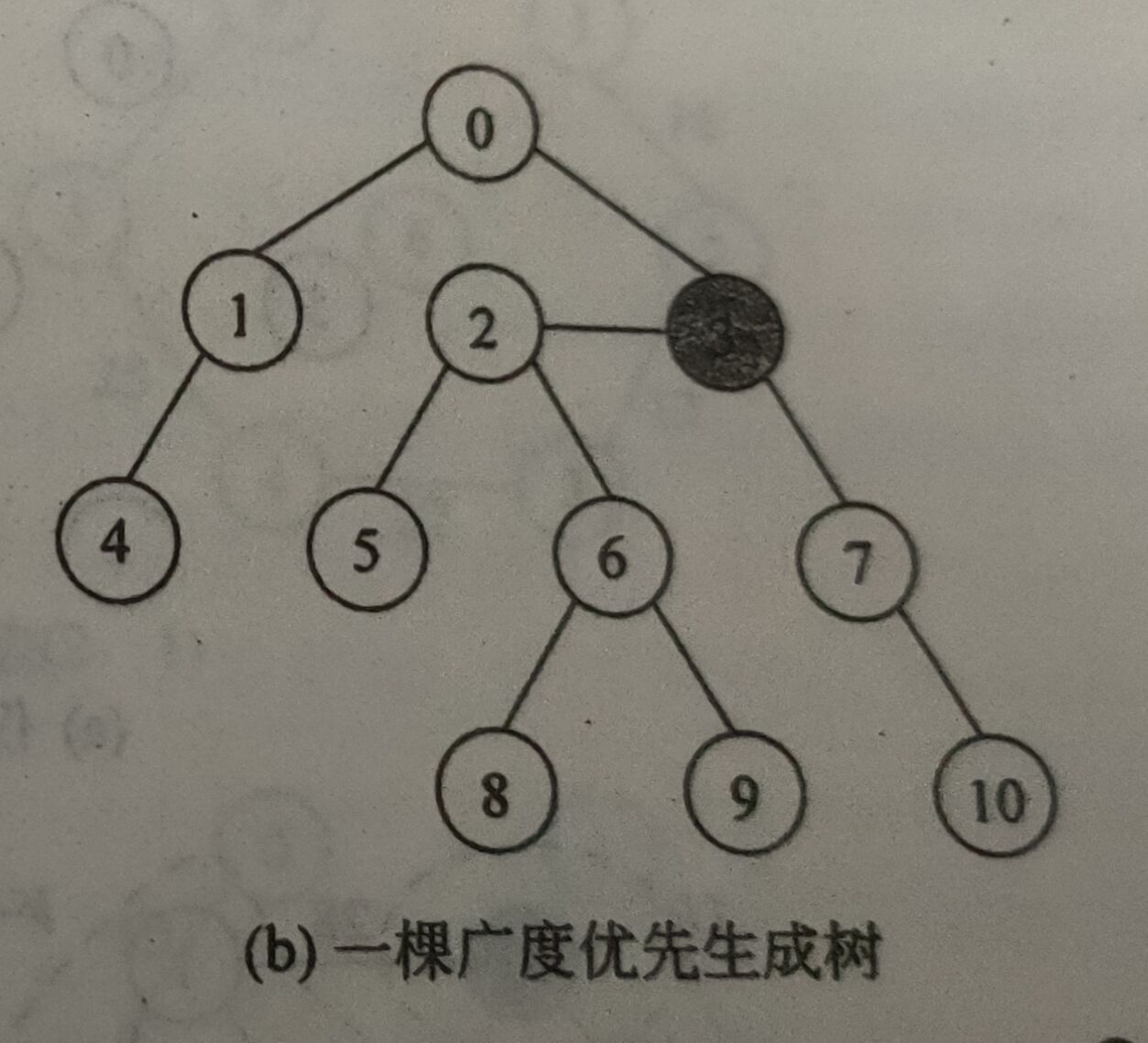
广度优先树

这样的生成树由遍历时访问过的n个顶点和遍历时经历的(n-1)条边组成。

对于非连通图,每个连通分量中的顶点集和遍历时走过的边一起构成一棵生成树,各个连通分量的生成树组成非连通图的生成森林。

普里姆算法

普里姆算法是一种构造性算法。假设G=(V,E)是一个具有n个顶点的带权连图,T=(U,TE)是G的最小生成树,其中U是T的顶点集,TE是T的边集,则由G构造从起始点V出发的最小生成树T的步骤如下:

(1)初始化U={v},以U到其他顶点的所有边为候选边。

(2)重复以下步骤(n- 1)次,使得其他(n-1)个顶点被加入到U中。

1）从候选边中挑选权值最小的边加人TE，设该边在V-U中的顶点是k，将k加入u。

2）考查当前U忠的所有顶雷修改候选边,若(k,j)的权值小于原来和顶点，联的候选边,则用(k,j)最代后署作为候选边。

void prim(int start)
{
int sumweight=0;
int i,j,k=0;
for(i=1;i<VNUM;i++) //顶点是从1开始
{
lowcost[i]=edge[start][i];
addvnew[i]=-1; //将所有点至于Vnew之外,V之内，这里只要对应的为-1，就表示在Vnew之外
}
addvnew[start]=0; //将起始点start加入Vnew
adjecent[start]=start;
for(i=1;i<VNUM-1;i++)
{
int min=MAX;
int v=-1;
for(j=1;j<VNUM;j++)
{
if(addvnew[j]!=-1&&lowcost[j]<min) //在Vnew之外寻找最短路径
{min=lowcost[j];
v=j;}
}
if(v!=-1)
{
printf("%d %d %d\n",adjecent[v],v,lowcost[v]);
addvnew[v]=0; //将v加Vnew中
sumweight+=lowcost[v]; //计算路径长度之和
for(j=1;j<VNUM;j++)
{if(addvnew[j]==-1&&edge[v][j]<lowcost[j])
{
lowcost[j]=edge[v][j]; //此时v点加入Vnew 需要更新lowcost
adjecent[j]=v;}
}
}
}
printf("the minmum weight is %d",sumweight);
}

ps:普利姆算法适用于稠密图。

克鲁斯卡尔算法

克鲁斯卡尔算法是一种按权值的的方法。假设G=(V.E)是一个具有n个顶点的带权连通无向图，T=(U,TE)是G的最小生成树，则构造最小生成树的步骤如下:

(1)置U的初值为V(即包含有G中的全部顶点),TE的初值为空集(即图T中的每一个顶点都构成一个分量)。

(2)将图G中的边按权值从小到大的顺序依次选取,若选取的边未使生成树T形成回路，则加人TE,否则舍弃,直到TE中包含(n- 1)条边为止。

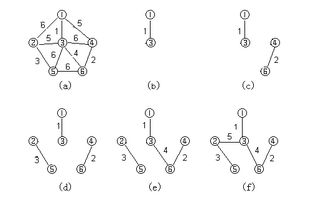
对于带权连通图,采用克鲁斯卡尔算法构造最小生成树的过程如下:

(1)将所有边按权值递增排序；

(2)图中边上的数字表示该边是第几小的边，如1表示是最小的边,2表示是第2小的边,依此类推。

void kruskal(MGraph G)
{
int i,j,u1,v1,sn1,sn2,k;
int vset[VertexNum]; //辅助数组，判定两个顶点是否连通
int E[EdgeNum]; //存放所有的边
k=0; //E数组的下标从0开始
for (i=0;i<G.n;i++)
{
for (j=0;j<G.n;j++)
{
if (G.edges[i][j]!=0 && G.edges[i][j]!=INF)
{ E[k].u=i;
E[k].v=j;
E[k].w=G.edges[i][j];
k++;}
}
}
heapsort(E,k,sizeof(E[0])); //堆排序，按权值从小到大排列
for (i=0;i<G.n;i++) //初始化辅助数组
{ vset[i]=i;}
k=1; //生成的边数，最后要刚好为总边数
j=0; //E中的下标
while (k<G.n)
{
sn1=vset[E[j].u];
sn2=vset[E[j].v]; //得到两顶点属于的集合编号
if (sn1!=sn2) //不在同一集合编号内的话，把边加入最小生成树
{printf("%d ---> %d, %d",E[j].u,E[j].v,E[j].w);
k++;
for (i=0;i<G.n;i++)
{ if (vset[i]==sn2)
vset[i]=sn1;
}
}
j++;
}
}

ps:克鲁斯卡尔算法适用于稀疏图。

最短路径

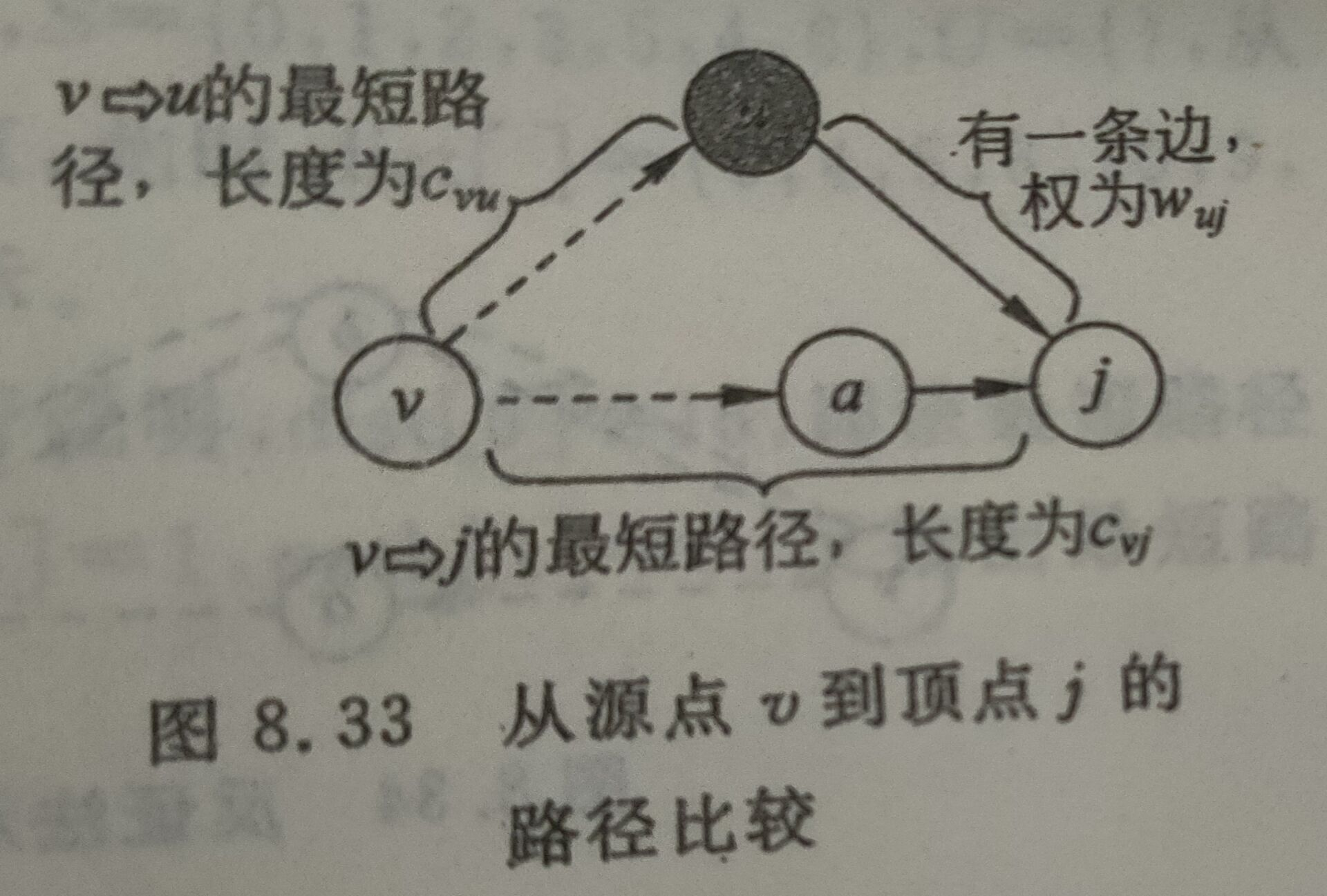
在一个不带权图中,若从一顶点到另一顶点存在着条路径，则称该路径长度为该路径上所经过的边的数目，它等于该路径上的顶点数减1。由于从一顶点到另一顶点可能存在着多条路径,每条路径上所经过的边数可能不同，即路径长度不同,把路径长度最短(即经过的边数最少)的那条路径称为最短路径,其长度称为最短路径长度或最短距离。

对于带权图,考虑路径上各边上的权，则把一条路径上所经边的权之和定义为该路名为路径长度。从源点到终点可能有不止一条路径，把路径长度最小的那条路径称为最短路名其路径长度(权之和)称为最短路径长度。

实际上，只要把不带权图上的每条边看成是权值为1的边,那么不带权图和带权图的量短路径和最短距离的定义就一致了。求图的最短路径有两个方面的问题，即求图中某一 顶点到其余各顶点的最短路径材图中每一对顶点之间的最短路径。

拓扑排序

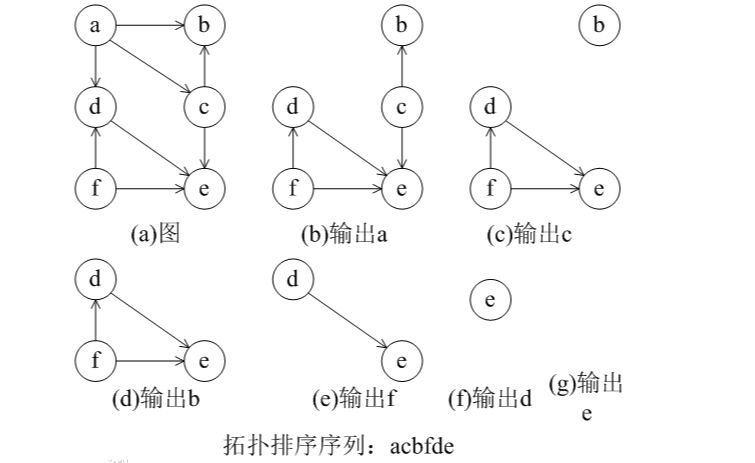
在一个有向图中找一个拓扑序列的过程叫拓扑排序。
拓扑排序方法如下:

(1)从有向图中选择一个没有前驱(即入度为0)的顶点并且输出它。

(2)从图中删去该顶点，并且删去从该顶点发出的全部有向边。

(3)重复上述两步，直到剩余的图中不再存在没有前驱的顶点为止。

这样操作的结果有两种: 一种是图中全部顶点都被输出,即该图中所有顶点都在拓扑序列中,这说明图中不存在回路（即该图为有向无环图）；另一种就是图中顶点未被全部输出，这说明图中存在回路。

queueq;
vectoredge[n];
for(int i=0;i<n;i++) //n 节点的总数
if(in[i]0) q.push(i); //将入度为0的点入队列
vectorans; //ans 为拓扑序列
while(!q.empty())
{
int p=q.front(); q.pop(); // 选一个入度为0的点，出队列
ans.push_back(p);
for(int i=0;i<edge[p].size();i++)
{
int y=edge[p][i];
in[y]--;
if(in[y]0)
q.push(y);
}
}
if(ans.size()==n)
{
for(int i=0;i<ans.size();i++)
printf( "%d ",ans[i] );
printf("\n");
}
else printf("No\n"); // ans 中的长度与n不相等，就说明无拓扑序列

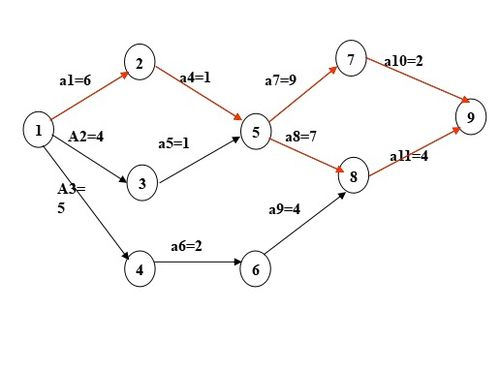
AOE网和关键路径

图中入度为0的顶点表示工程的开始事件(如开工仪式),出度为0的顶点表示工程结束事件，称这样的有向图为边表示活动的网(AOE网)。

利用这样的AOE网能够计算完成整个工程预计需要多少时间，并找出影响工程进度的“关键活动”,从而为决策者提供修改各活动的预计进度的依据。

在AOE网中，从源点到汇点的所有路径中具有最大路径长图的路径称为关键路径，完成整个工程的最短时间就是AOE网中关健路径的长度，或者说是AOE中一条关键路径上各活动持续时间的总和，把关路径上的活动称为关键活动。

因此，只要找出AOE网中的所有关键活动也就找到了全部关键路径。