软工个人项目(图形交点)
个人项目作业——求图形交点
| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里 | 个人项目作业 |
| 教学班级 | 006 |
| 项目链接 | https://github.com/notasadsong/intersection |
一、PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 90 | 150 |
| · Design Spec | · 生成设计文档 | 15 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 20 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 15 | 30 |
| · Design | · 具体设计 | 30 | 30 |
| · Coding | · 具体编码 | 150 | 150 |
| · Code Review | · 代码复审 | 20 | 40 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 120 |
| Reporting | 报告 | 60 | 90 |
| · Test Report | · 测试报告 | 20 | 20 |
| · Size Measurement | · 计算工作量 | 20 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 10 | 20 |
| 合计 | 520 | 740 |
第一次编写c++程序,对语言熟悉不足,熟悉语言的时间比想象中的要多很多,还有专门为了测试写了几个函数,测试上花的时间也大大超出预期。
二、解题思路描述
采用暴力枚举法,对每一条直线或圆,都去和其他直线或圆求交点,得到的结果存入set,利用set去重后set中的元素的个数就是交点的个数。具体交点的求法如下:
1、直线与直线交点
两直线交点坐标可以直接通过数学公式的推导求得:
两个直线的一般式:
联立求解可得:
当两直线平行时没有交点,即$$ ae=bd $$,此时不用求解直接返回。
2、直线与圆交点
先计算出圆心到直线距离 d ,找到圆心在该直线上的投影点。然后分三种情况讨论:
- 若 d 大于半径 r ,无交点。
- d 等于半径 r ,交点只有一个,为投影点。
- d 小于半径 r ,交点有两个,采用圆与直线的交点的方法算出。
3、圆与圆交点
先计算出圆心距 d ,两圆中较大的半径为 R ,较小的为 r ,然后分三种情况讨论:
- d 大于 R + r ,外离圆,无交点。
- d 小于 R - r ,一个圆包含于另一个圆,无交点。
- 除上述之外的情况皆有交点。将两圆的标准方程相减得到一条直线方程,问题转化为求该直线与圆的交点,可以有前述方法求得。
三、设计实现过程
1、本次作业中我创立了三个类,分别是:Point, Line, Circle,用于存储交点,直线和圆。求交点的方法都内置于类中,通过调用可以实现全部交点的求解。
-
直线采用一般式的形式存储a,b, c,内置有方法求线线交点,具体如下:

-
圆的存储结构是圆心坐标和半径,内置有求圆圆交点和圆线交点方法,代码如下:
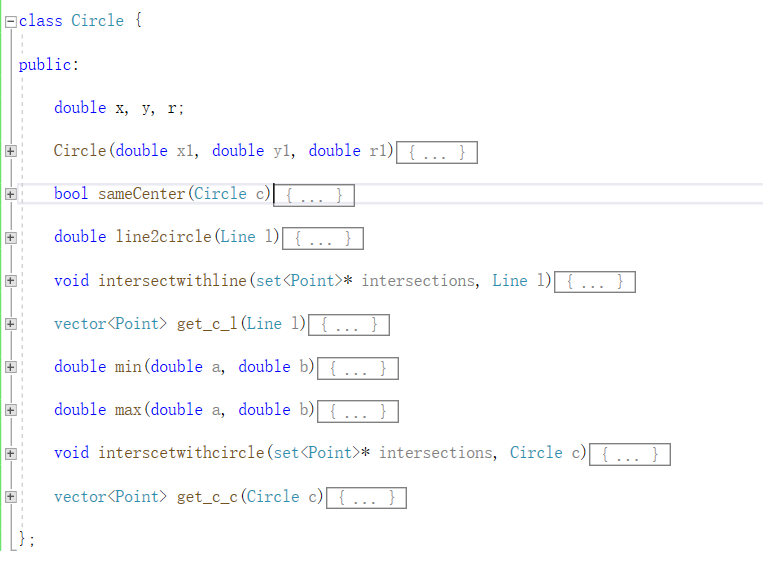
-
点的结构存储了它的x,y坐标,同时在点中重载了 "<" 操作符用于在set中进行比较,代码如下:

2、单元测试的设计
- 对于直线求交点,设计了平行线、相交线等测试
- 对于直线与圆求交点,设计了相离、相切、相交三种情况,其中还包括直线与y轴平行的特殊情况
- 对于圆与圆求交点,实际了外离,外切,相交,内切,内含五种情况
结果均符合预期。
四、性能分析
由于使用的是暴力法,因此肯定因为遍历产生很大的cpu开销,代码分析的结果也证实了这一点。百分之九十以上的cpu资源是耗费在循环求交点的过程中,也就是最多使用的intesect函数,如图所示:
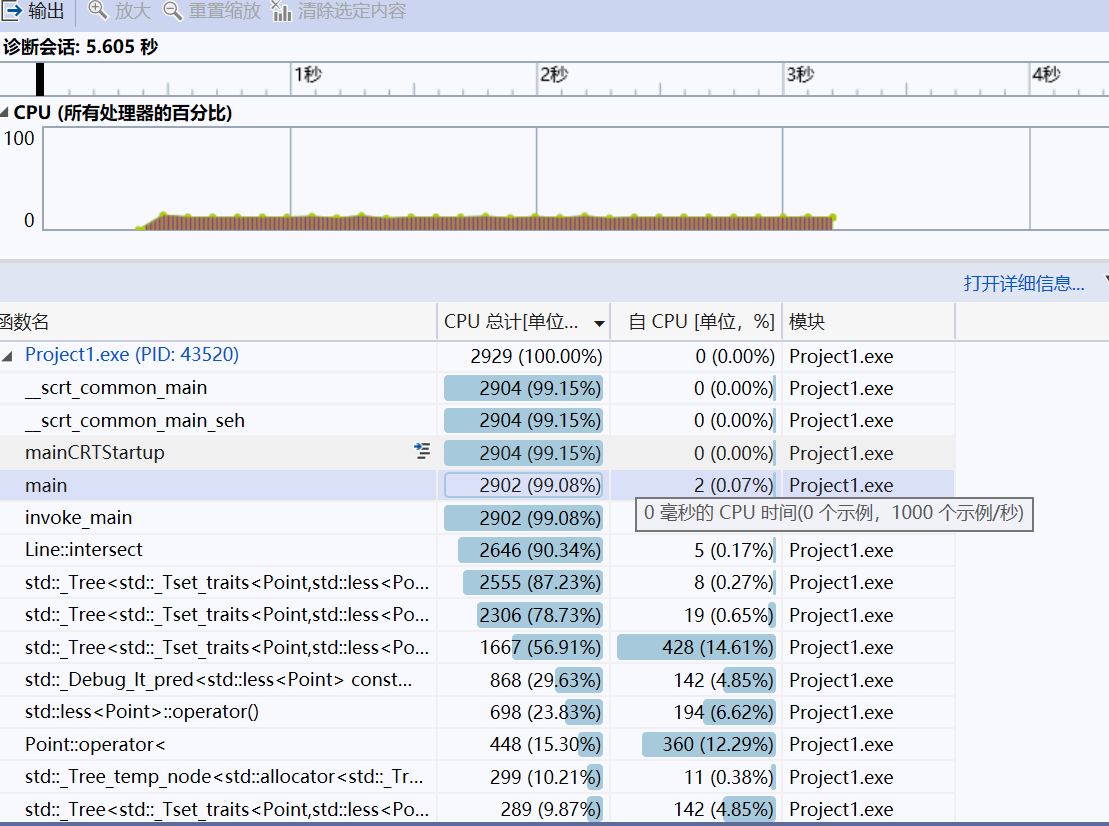
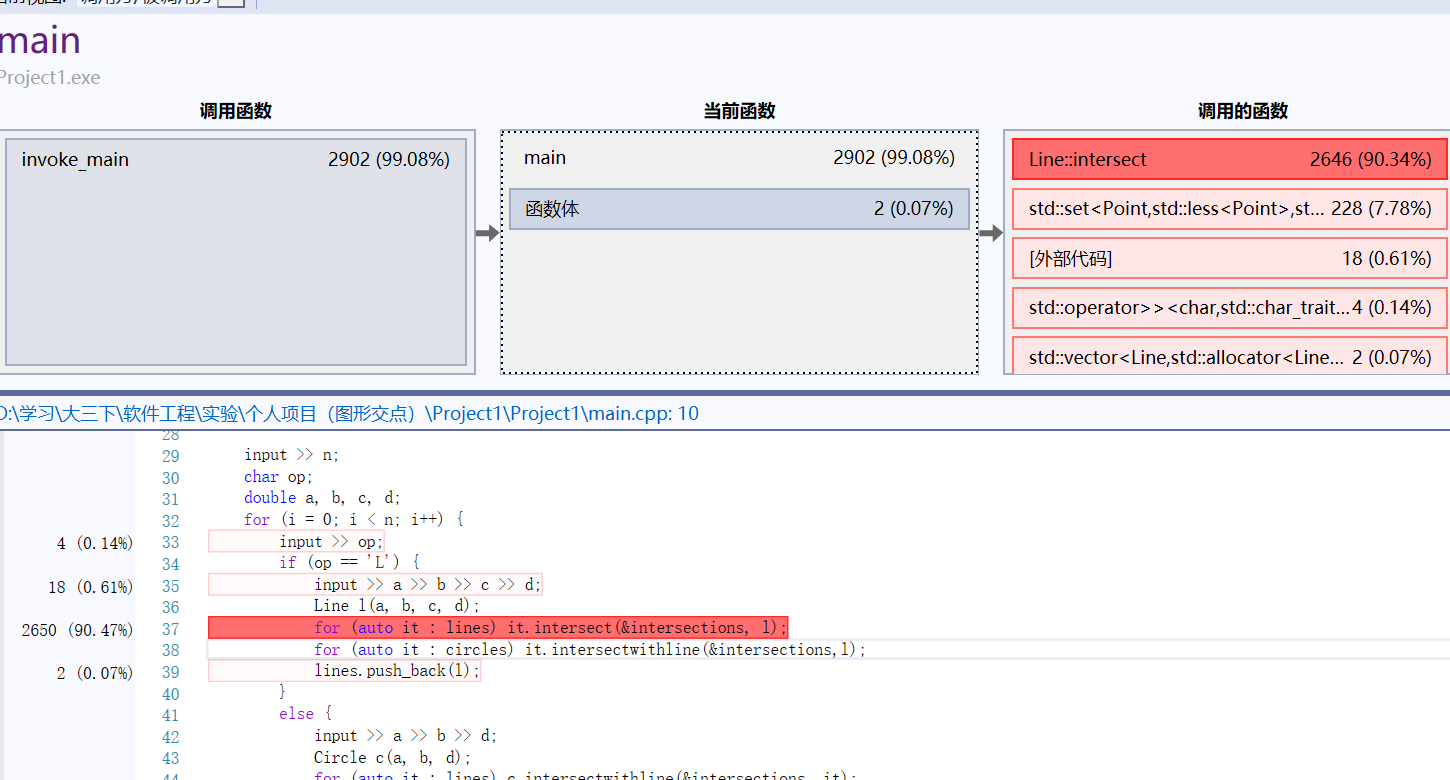
但这已经是经过剪枝处理的n^2复杂度方法了。同时我也考虑过可能是set内部排序也造成了资源的占用,可以尝试使用无序索引如哈希值,有可能会降低成本。至于更优化的个人没有去尝试,希望能在作业截至之后老师评选出优秀作业供大家借鉴学习。
五、代码说明
1、直线直线交点求解函数
直接带入数学公式求解,再次不过多赘述。
Point getLLintersection(Line l) {
double x = (l.c * b - c * l.b) / (a * l.b - l.a * b);
double y = (l.a * c - a * l.c) / (a * l.b - l.a * b);
return Point(x, y);
}
2、直线圆交点求解函数
先求出圆心到直线的距离,根据距离与半径的关系可以分为三类:相离,相切,相交。
相交时要特殊考虑与y轴平行的直线。
vector<Point> get_c_l(Line l) {
vector<Point> re;
double dis = line2circle(l);
if (dis > r) return re;
//先找到圆心在直线上的投影点,用与直线垂直的线做交点得到
Line l_(l.b, -l.a, y * l.a - x * l.b);
Point p = l_.getLLintersection(l);
if (dis < r) {
if (l.b == 0) {
Point p1(p.x, p.y + sqrt(r * r - dis * dis));
Point p2(p.x, p.y - sqrt(r * r - dis * dis));
re.push_back(p1);
re.push_back(p2);
return re;
}
else {
double delta_x = sqrt((r * r - dis * dis) * l.b * l.b / (l.a * l.a + l.b * l.b));
double k = -(l.a / l.b);
Point p1(p.x + delta_x, p.y + k * delta_x);
Point p2(p.x - delta_x, p.y - k * delta_x);
re.push_back(p1);
re.push_back(p2);
return re;
}
}
else {
re.push_back(p);
return re;
}
}
3、圆圆交点求解函数
分出两种情况,有交点和无交点。
无交点的情况不需要操作直接返回,有焦点的情况可以转化为直线和圆的交点求解。
vector<Point> get_c_c(Circle c) {
vector<Point> re;
double dis_center = sqrt((x - c.x) * (x - c.x) + (y - c.y) * (y - c.y));
//外离
if (dis_center > r + c.r) return re;
//包含
if (dis_center < max(r, c.r) - min(r, c.r)) return re;
//有交点
double a_ = -2 * (x - c.x);
double b_ = -2 * (y - c.y);
double c_ = x * x + y * y - r * r - c.x * c.x - c.y * c.y + c.r * c.r;
Line l_(a_, b_, c_);
re = get_c_l(l_);
return re;
}
六、截图