五种排序算法---插入排序

一、直接插入排序

基本思想：每一步将一个待排序的数据插入到当前已经排好序的有序序列中，直到插完所有元素为止。

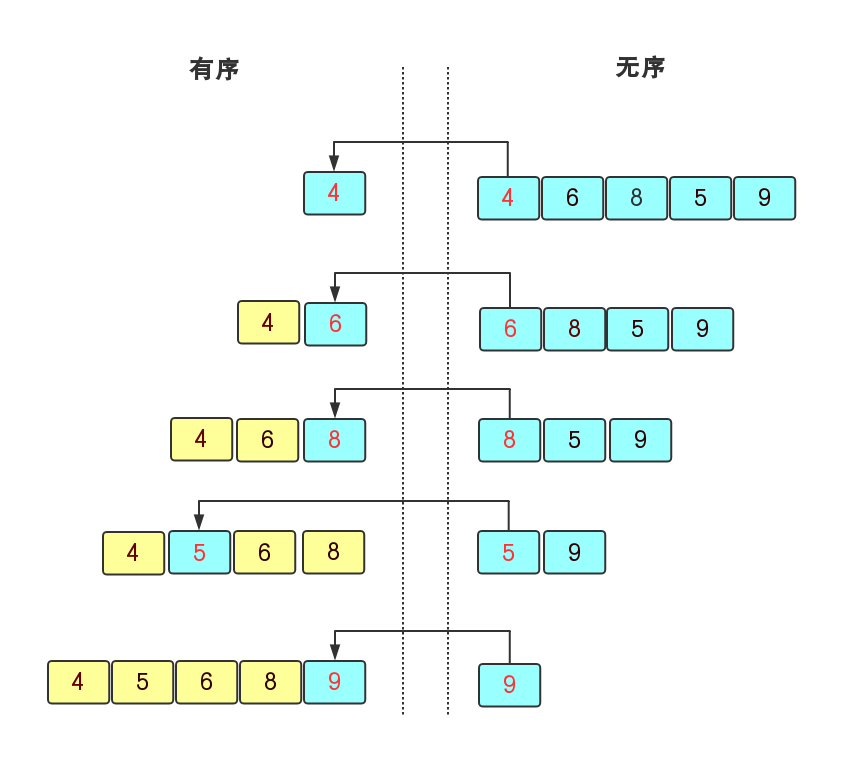
算法实现：直接插入排序是将无序序列中的数据插入到有序的序列中，在遍历无序序列时，首先拿无序序列中的首元素与有序序列中的每一个元素比较并插入到合适的位置，一直到无序序列中的所有元素插完为止。对于一个无序序列[4,6,8,5,8]来说，我们首先先确定首元素4是有序的，然后在无序序列中向右遍历，6大于4则它插入到4的后面，在继续遍历到8，8大于6则插入到6的后面，这样继续直到得到有序序列[4,5,6,8,9]。

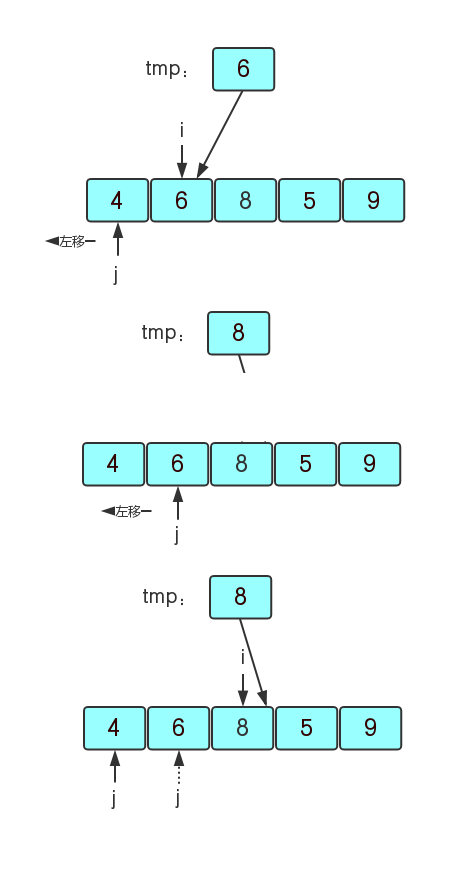
1、用一个变量tmp存放关键字，因为我们先确定第一个元素是暂时有序的，所以tmp存放无序序列中的第二个元素，然后i开始也为第二个元素的下标，j则为i-1，因为j要用有序的区域元素来与无序的区域元素比较。那么一开始i=1,tmp=6,j=0,因为6>4,所以就不能进行插入；然后i向右走，i=2,tmp=arr[2]=8,j=i-1=1,8>6>4也不用插入。

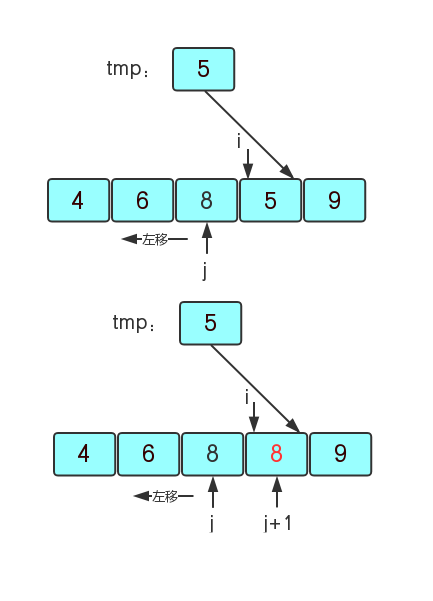
2）i继续向右走，i=3，tmp=arr[3]=5,j=i-1=2,5<8则要将8给5所在的元素，j向左走，继续遍历有序区域。

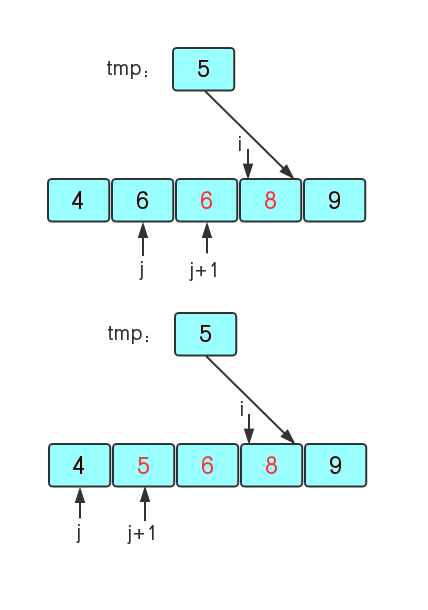
3）当j向右走到6时发现6>tmp=5,所以将6给它右边的第一个值(j+1的位置)，再继续遍历所有有序区域，j=0时发现4<5,则j+1的位置就是5该在的位置，那么就将tmp的值给j+1的位置的元素。

4）再继续上面的操作，i最后到9发现比前面有序区域的元素都大，则不用再插入了，这样就得到了一个有序序列{4,5,6,8,9}。

 二、希尔排序（shell排序）

基本思想：希尔排序就是把序列按下标的一定增量分组，对每组使用直接排序算法排序；随着增量的逐渐减少，每组包含的关键字越来越多，当增量减至1时，整个序列恰好被分为一组，算法便终止。

算法实现：希尔排序需要定义一个增量，这里选择增量为gap=length/2，缩小增量以gap=gap/2的方式，这个增量可以用一个序列来表示，{n/2,(n/2)/2...1},称为增量序列，这个增量是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。

1）对于一个无序序列{8,9,1,7,2,3,5,4,6,0}来说，我们初始增量为gap=length/2=5，所以这个序列要被分为5组，分别是{8,3},{9,5},{1,4},{2,0},对这5组分别进行直接插入排序，则小的元素就被调换到了前面，然后再缩小增量gap=gap/2=2。

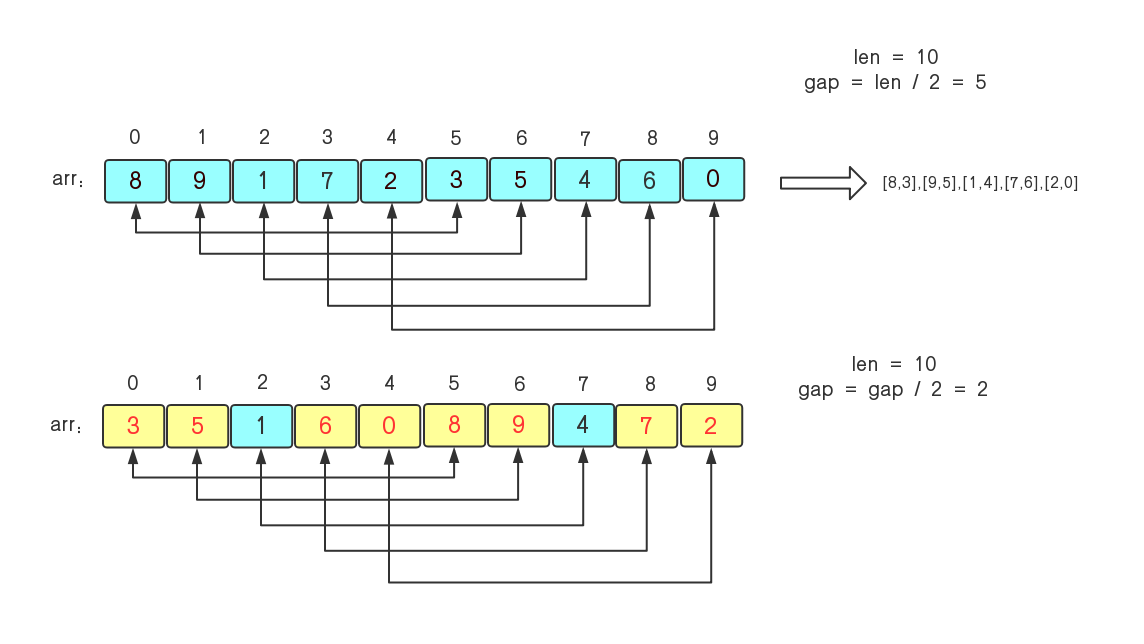
2）上面缩小完增量后，序列再次被分为2组，分别是{3,1,0,9,7}和{5,6,8,4,2}，再对这两者进行直接插入排序，那么就更加有序了。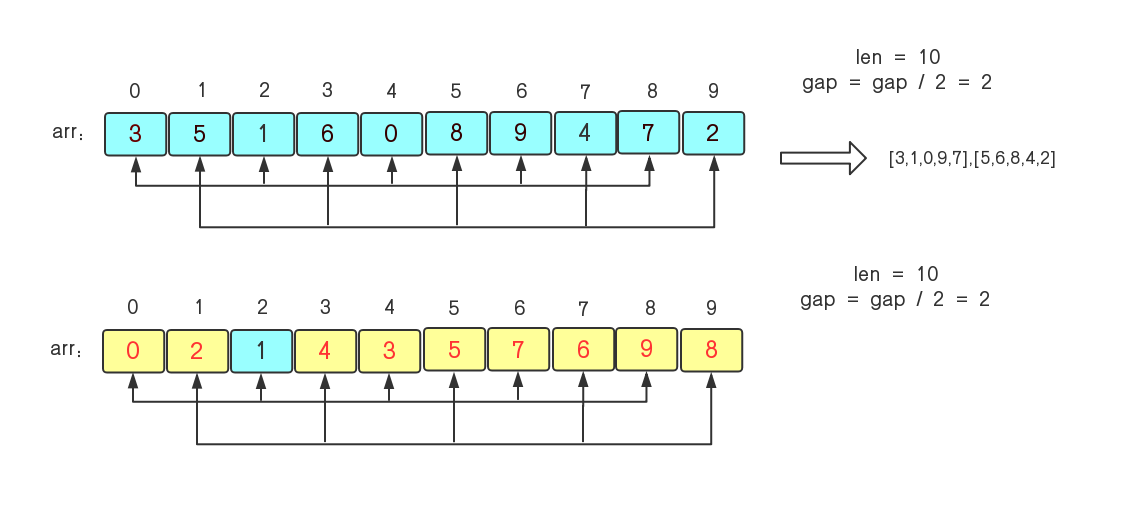

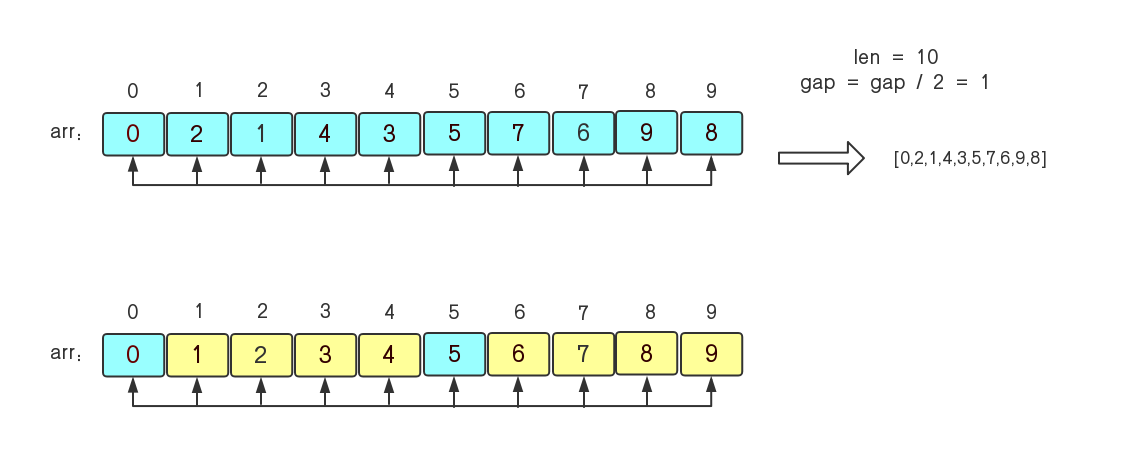
3）然后再缩小增量gap=gap/2=1，这时整个序列就被分为一组即{0,2,1,4,3,5,7,6,9,8},再进行调整，就得到了有序序列{0,1,2,3,4,5,6,7,8,9}。