五种排序算法--快速排序

一、步骤（从小到大排序）

1、在数组中选一个基准数（通常为数组第一个）。

2、将所有比基准值小的值摆放在基准的前面，所有比基准值大的摆放在基准的后面（相同的数可以放到任意一边）;在这个分区推出之后，该基准就处于数列的中间位置。

3、递归地把“基准值前面的子数列”和“基准值后面的子数列”进行排序。

下面以数列a=[30,40,10,20,50]为例，演示它的快速排序过程：

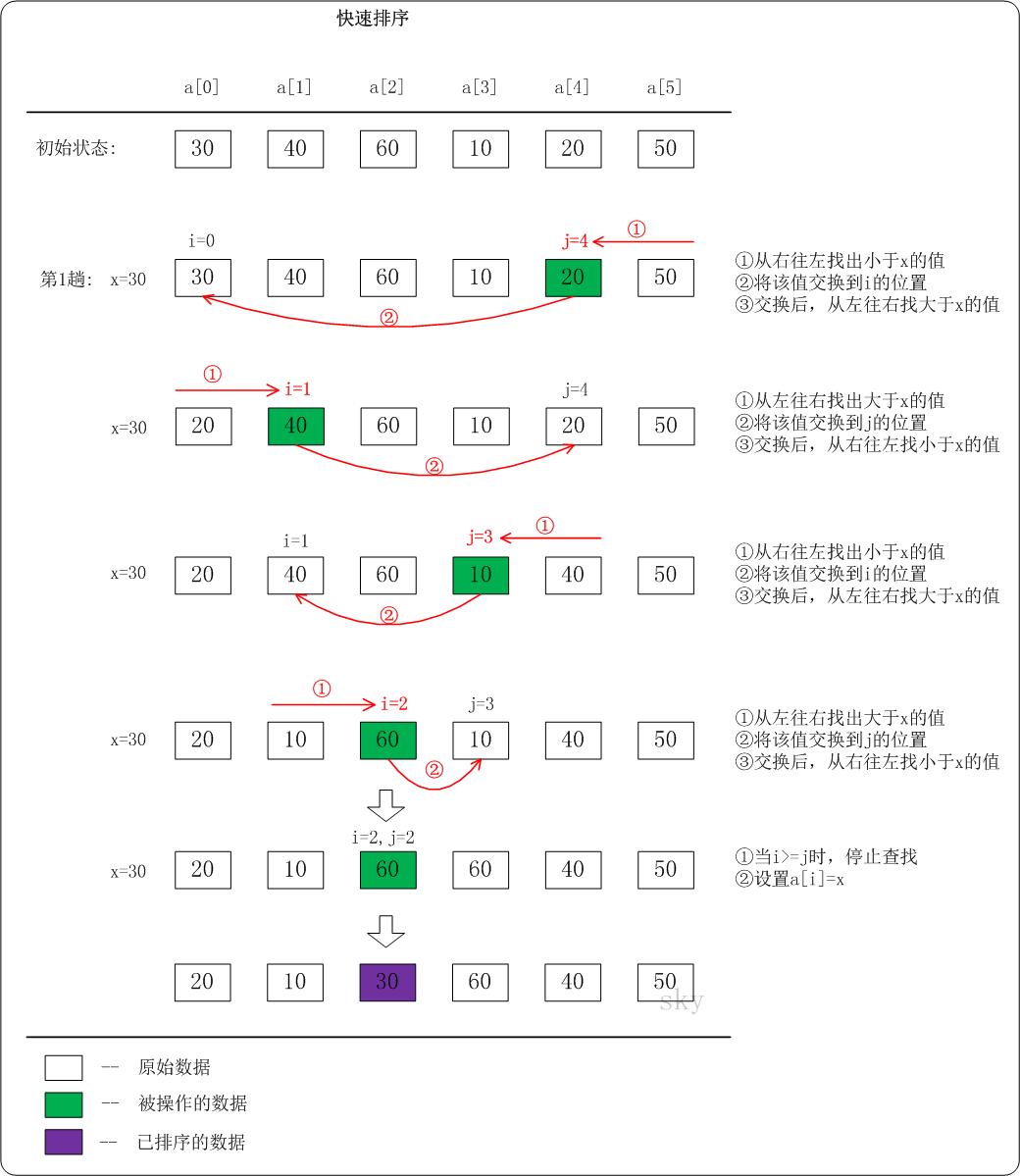
上图只是给出了第一趟快速排序的流程。在第一趟中，设置x=a[i],即x=30.

(01)从“右-->左”查找小于x的数；找到满足条件的数a[j]=20,此时j=4;然后将a[j]赋值a[i],此时i=0;接着从左往右遍历。

(02)从“左-->右”查找大于x的数；找到满足条件的数a[i]=40,此时i=1；然后将a[i]赋值a[j],此时j=4;接着从右往左遍历。

(03)从“右-->左”查找小于x的数；找到满足条件的数a[j]=10,此时j=3；然后将a[j]赋值a[i],此时i=1;接着从左往右遍历。

(04)从“左-->右”查找大于x的数；找到满足条件的数a[i]=60,此时i=2；然后将a[i]赋值a[j],此时j=3;接着从右往左遍历。

(05)从“右-->左”查找小于x的数；没有找满足条件的数。当i>=j时，停止查找；然后将x赋值给a[i]。此趟遍历结束！

(06)安装同样的方法，对子数列进行递归遍历。最后得到有序数组。

二、快速排序的时间复杂度和稳定性

快速排序稳定性

快速排序是不稳定的算法，它不满足稳定算法的定义。

算法稳定性---假设在数列中存在a[i]=a[j],若排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个算法是稳定的。

快速排序时间复杂度

快速排序的时间复杂度在最坏情况下是O(N^2)，平均的时间复杂度是O(N*lgN)。

这句话很好理解：

假设被排序的数列中有N个数。遍历一次的时间复杂度数O(N),需要遍历多少次呢？至少lg(N+1)次，最N次。

(01) 为什么最少数lg(N+1)次？快速排序数采用分治法进行遍历的，我们将它看作一颗二叉树，它需要遍历的次数就少二叉树的深度，而根据完全二叉树的定义，它的深度至少是lg(N+1)。因此，快速排序的遍历次数最少数lg(N+1)次。

(02)为什么最多数N次？这个应该非常简单，还是将快速排序看作一颗二叉树，它的深度最大是N。因此，快速排序的遍历次数最多是N次。