五种排序算法之--堆排序
一、部分概念
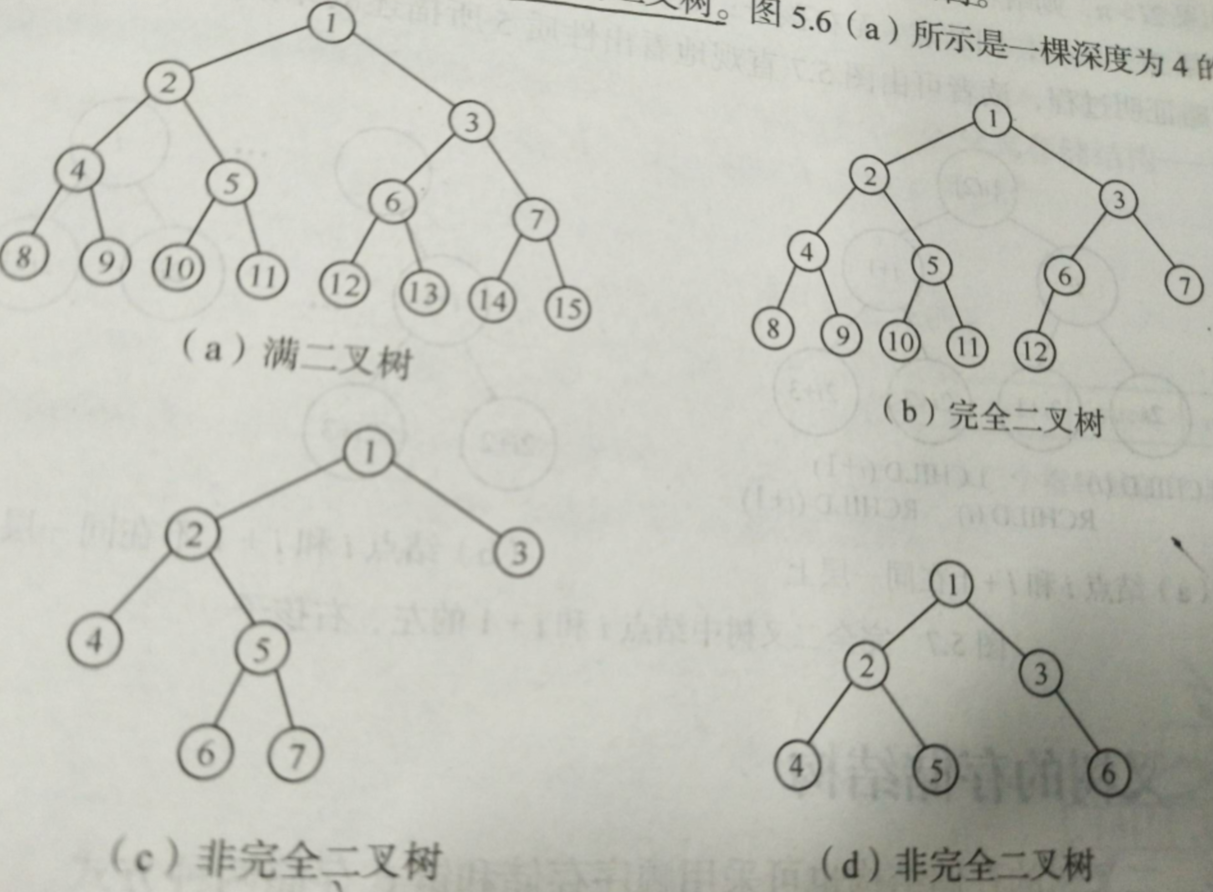
满二叉树:深度为k,且含有(2^k)-1个节点的二叉树。
完全二叉树:深度为k,又n个结点,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的节点一一对应时,称为完全二叉树。
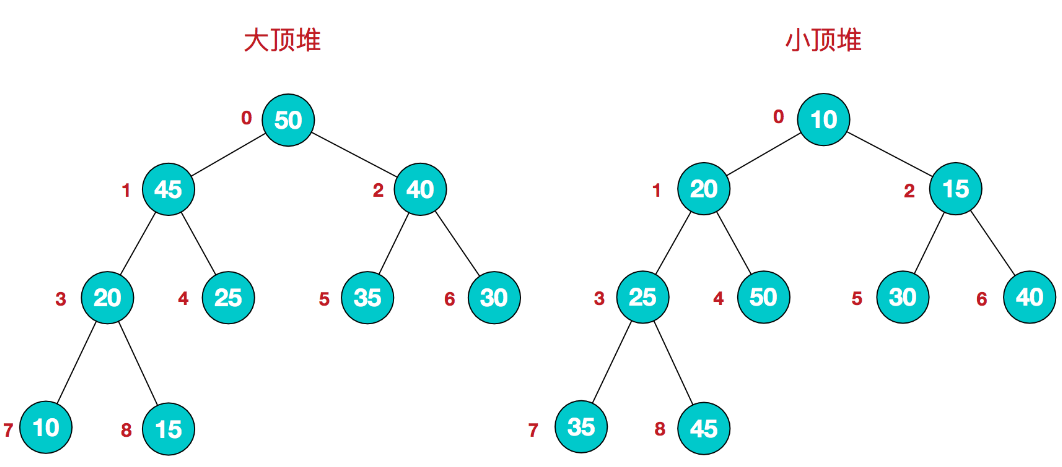
堆的结构可以分为大根堆和小根堆,是一个完全二叉树。
每个节点的值都大于其左孩子和又孩子节点的值,称之为大根堆;每个节点的值都小于其左孩子和右孩子节点的值,称之为小根堆。(它们右孩子值和左孩子值谁的值大,谁的值小没有要求)
1、父节点索引:(i-1)/2 (这里计算机中的除以2,省略掉小数)
2、左孩子索引:2*i+1;
3、右孩子索引:2*i+2
二、堆排序过程
升序---使用大顶堆
降序---使用小顶堆
思想(这里使用大顶堆)
假设要对一个有n个元素的数组进行排序。我们先把这个数组里面的前n个数据拿出来构建一个大顶堆。这个时候我们肯定能保证堆顶那个元素树最大的。然后我们把那个最大的元素放在数组的倒数第一个位置。然后再堆数组里面的前n-1个元素再构建一次大顶堆,这个时候再把堆顶元素拿出来放到数组倒数第二个位置。依次进行n-1次就完成堆排序过程。
如何把一个二叉树弄成大顶堆呢?
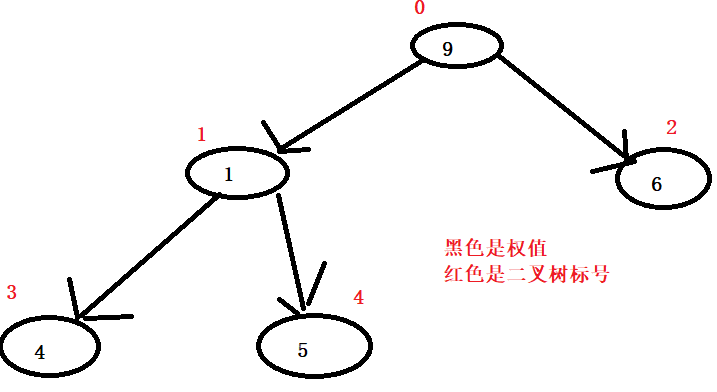
由上面这个图我们可以知道它的数组中元素顺序是这样的:【9,1,6,4,5】
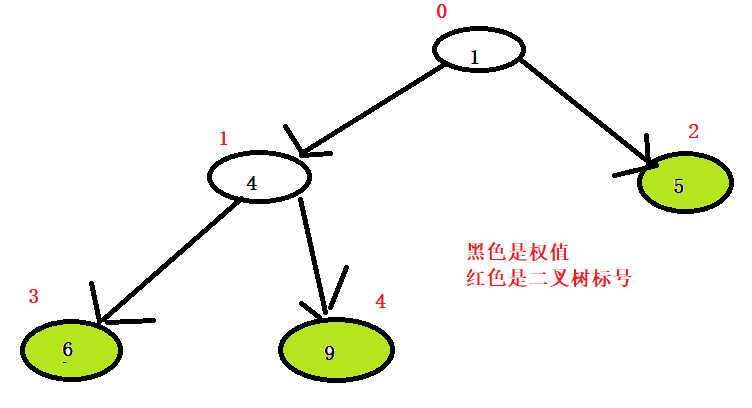
我们发现1号位置上的权值并不大于它的儿子的权值,所以我们给它的左右儿子中那个权值最大的儿子交换。
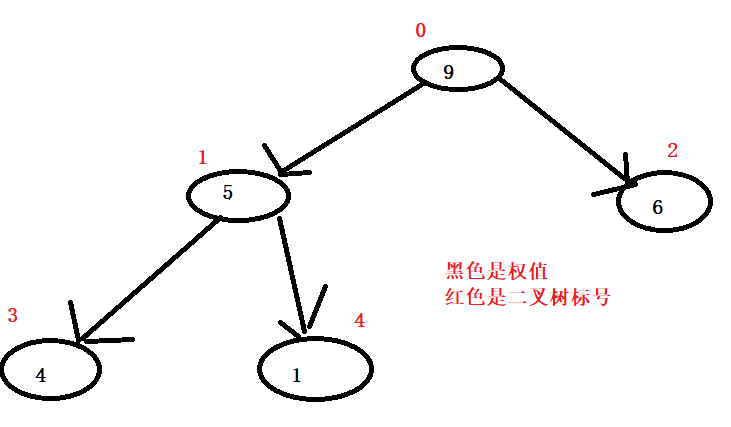
这个时候我们知道最大权值是9,那就让最大权值放在数组的倒数第一个位置,让倒数第一位置的权值和它交换一下。
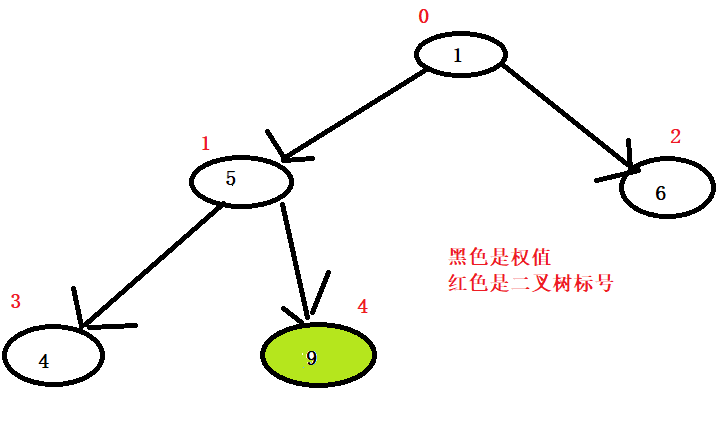
这个时候原数组就变成了:【1,5,6,4,9】,然后就接着对这个二叉树改造,使它变成大顶堆(这个时候第4个位置就不再参与)
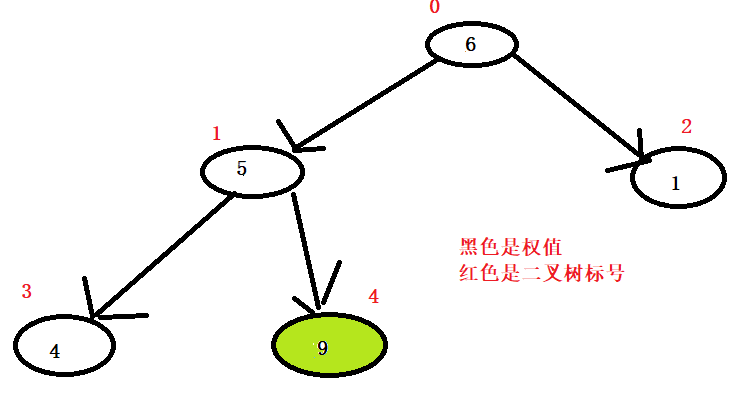
发现这样就是一个大顶堆了。
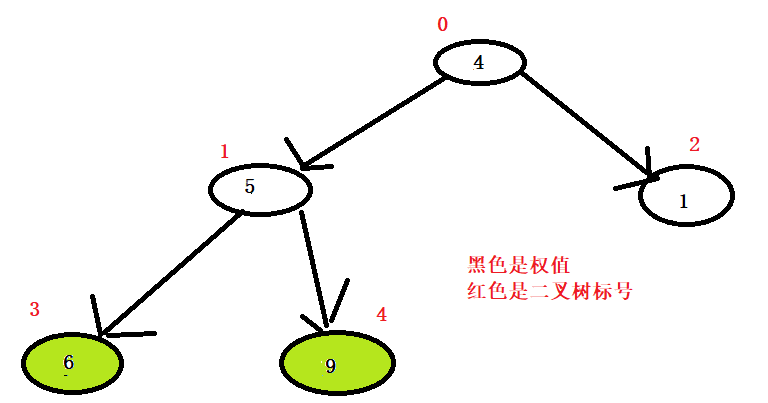
数组:【4,5,1,6,9】
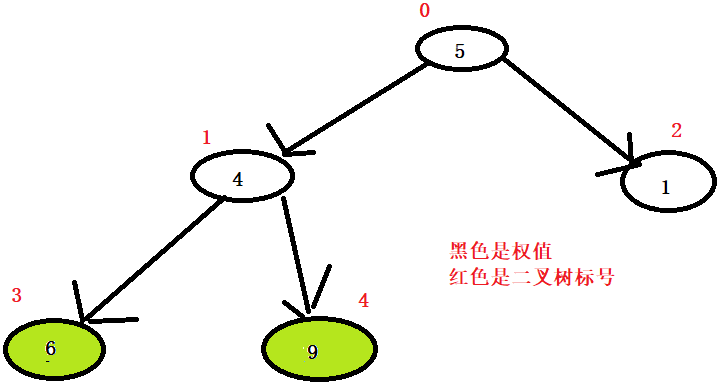
又变成了大顶堆
数组:【1,4,5,6,9】
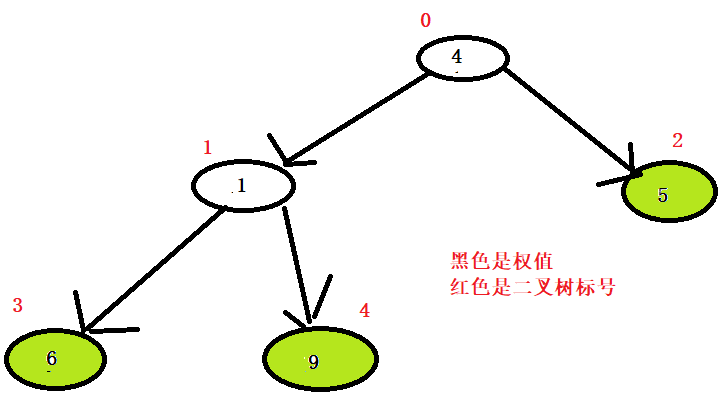
又变成了大顶堆
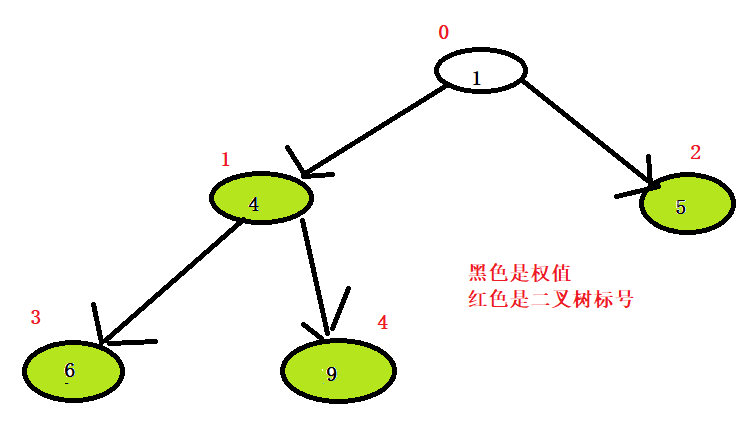
数组:【1,4,5,6,9】
循环了5-1次,所以该结束了。
最后的结果就是【1,4,5,6,9】


