R-B Tree

1、简介

R-B Tree，全称Red-Black Tree，又称为“红黑树”，为一种自平衡二叉查找树（特殊的平衡二叉树，都是在插入和删除操作时通过特定操作保持二叉树的平衡，从而获得较高的查找性能）。红黑树的每个节点上都有表示存储位的颜色，可以是红色（Red）或黑色（Black）。

红黑树特性：

• (1)每个节点要么是黑色，要么是红色。
• (2)根结点必须是黑色。
• (3)每个叶子结点是黑色（叶结点即指树尾端NIL指针或NULL结点）。
• (4)不能有连续的两个红色结点。
• (5)对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包括相同数目的黑结点。

正是红黑树的这5条性质，使得一颗n个结点的红黑树保持了Log n的高度，从而解释了红黑树的查找、插入、删除的时间复杂度最坏为O(Log n)这一结论成立的原因。

红黑树示意图一：

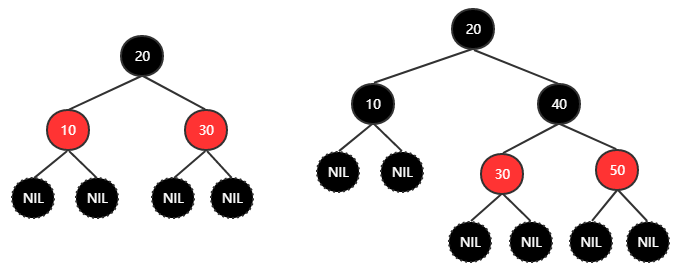
红黑树示意图二：

特性4表明：红色结点的父、左子、右子只能是黑色结点，红色和红色不能连接在一起；而黑色无论红色还是黑色都可以连在一起。（红色暴脾气互不相融，黑色和蔼可亲谁来都行）。

特性5表明：随便选一个结点，不论怎么走，走到最后叶子结点时，其经过的黑色结点数量都是相等的（所谓完全黑平衡）。

特性4、5共同决定了：最长路径的节点数量不会超过最短路径的两倍。因为黑色节点数量要一样，红色不能连着来，从而路径全黑时最短，红黑交替时最长。例如：四个黑色结点，最短：黑-黑-黑-黑（4），最长：黑-红-黑-红-黑-红-黑（7）。因为路径长度（高度）有了一定限制，所以称红黑树是有一定平衡性的，不会出现极端倾斜的情况。 

2、红黑树应用

主要用来存储有序数据，时间复杂都为O(log n)，效率非常高。如Java集合中的TreeMap、TreeSet、ConcurrentHashMap，C++中Set、map，以及Linux虚拟内存的管理都是用红黑树去实现的。

3、树的旋转

红黑树的基本操作是添加和删除。对红黑树进行添加和删除操作之后，红黑树会发生变化，此时可能不满足红黑树的5条特性。所以需要通过旋转来使这棵树重新成为红黑树。旋转操作包括：左旋和右旋两种操作。

仔细观察左旋与右旋的示意图，可以清晰的发现这两个操作是对称的。无论是左旋还是右旋，被旋转的树在旋转前是二叉查找树，且在旋转之后仍然是一棵二叉查找树。

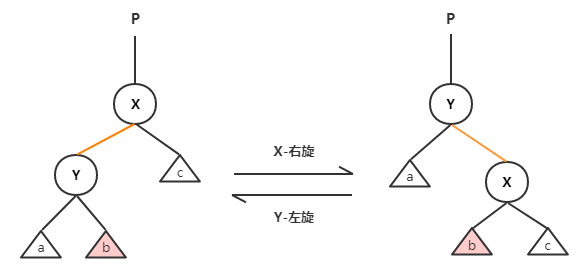
旋转后，原来“左小右大”的特点不会受到影响。影响的是左右子树的高度，右旋左子树高度-1，右子树高度+1；左旋右子树-1，左子树+1。

比如某棵树的左子树高度已经达到3，而右子树只有1，只要右旋一下，左右子树高度都将调整为2.整个树看来，高度就相当于降低了1（3->2），这样就是高度"平衡"。

注意b：

右旋前，b是挂在Y的右子，而右旋后，挂到了X的左子了；
左旋前，b是挂在X的左子，而左旋后，挂到了Y的右子了；

4、树的插入

开始之前，先约定名称：

红黑树属于二叉搜索树，插入动作也与二叉搜索树一致，只不过红黑树在插入之后，多了平衡动作（旋转与涂色）。

新插入的节点均为红色节点，因为红色不会影响路径上黑色节点的数量，保持性质4。如果父节点为黑色，就直接结束了；如果父节点为红色，则需要另外处理了。

以新插入的节点为当前平衡节点N，插入平衡大体上分为以下情形：

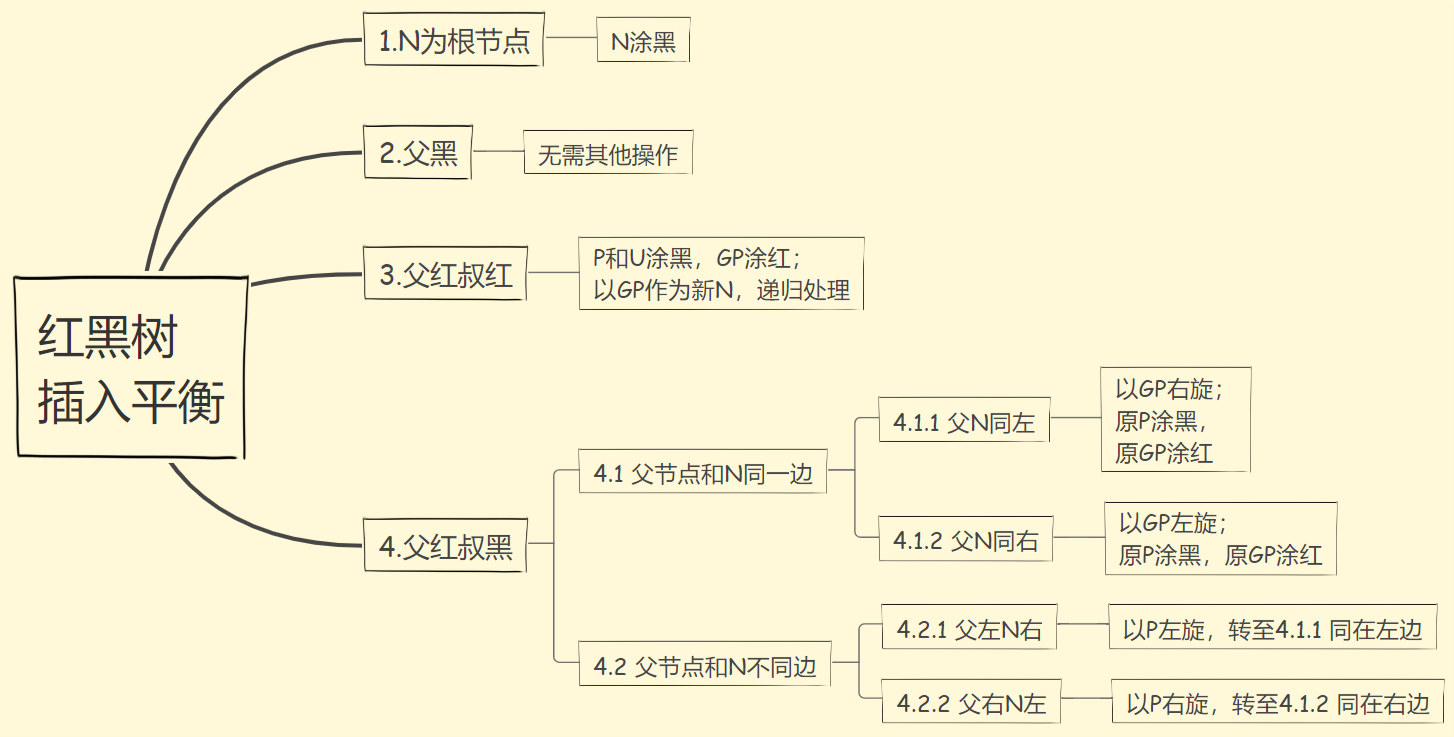
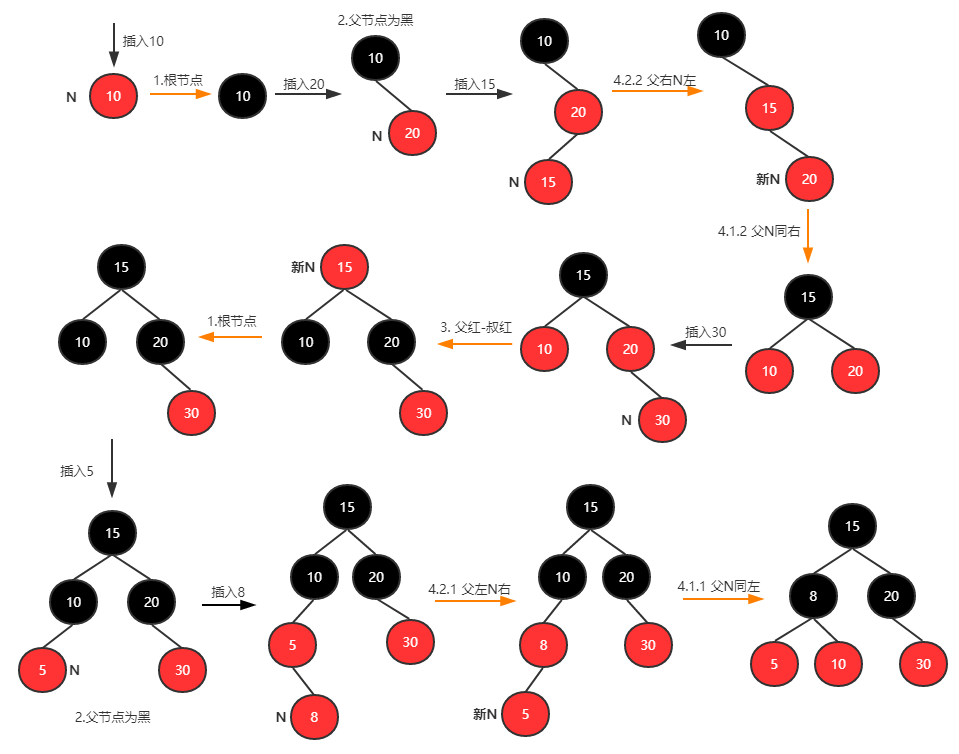
用例：插入10，20，15，30，5，8。步骤说明：

• N为根：涂黑完事；
• 父黑：啥事不用管；
• 父红叔红：父/叔涂黑，祖父涂红，然后把祖父当成新的平衡节点递归处理（我们下面平衡了，让他老人家和上面沟通吧）；
• 父红叔黑：父节点和新插入节点同一边的话，扭一下就完事了（同左右旋，同右左旋，顺便涂色）；不在同一边的话，先扭到同一边吧。

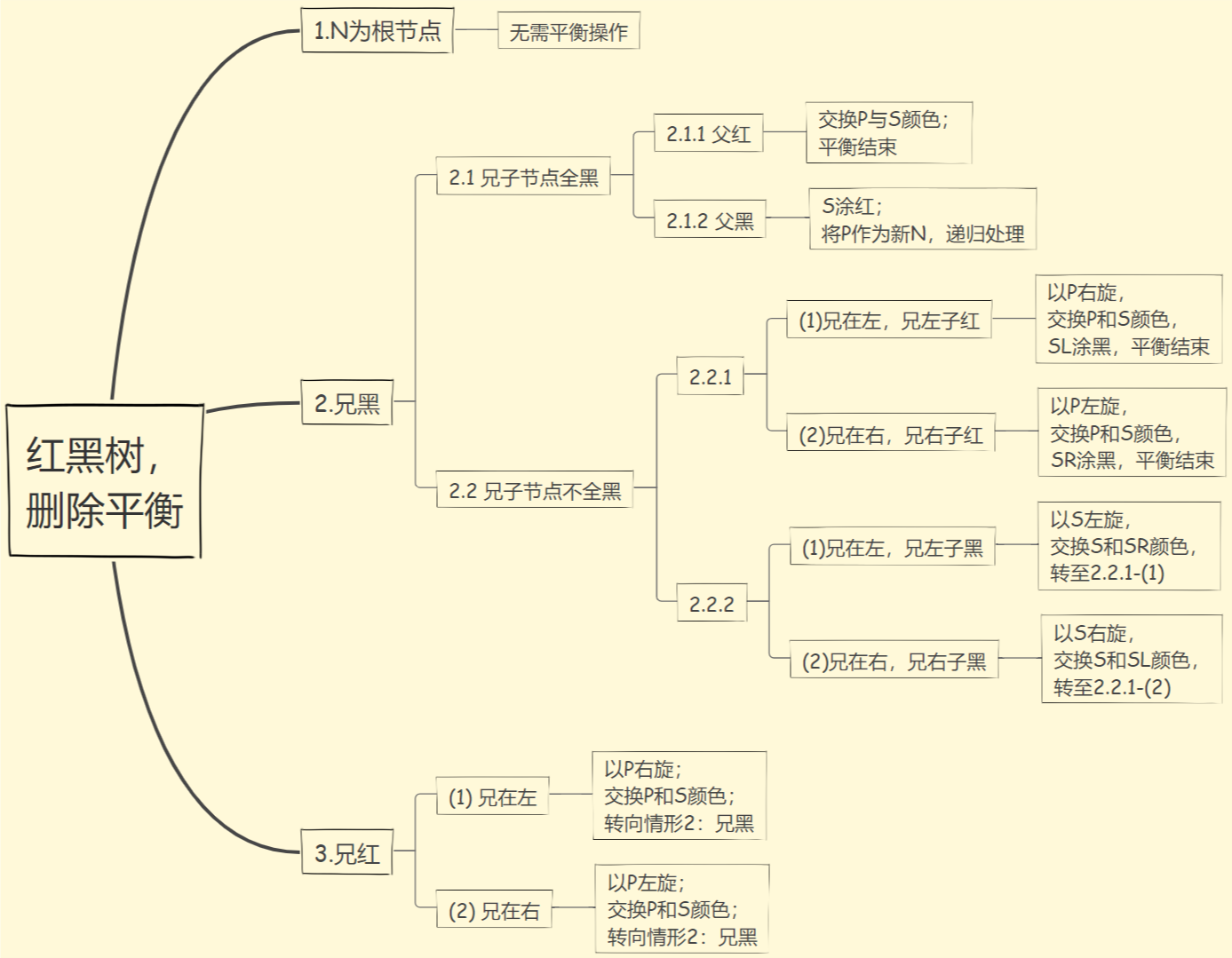
5）树的删除

情况分析：

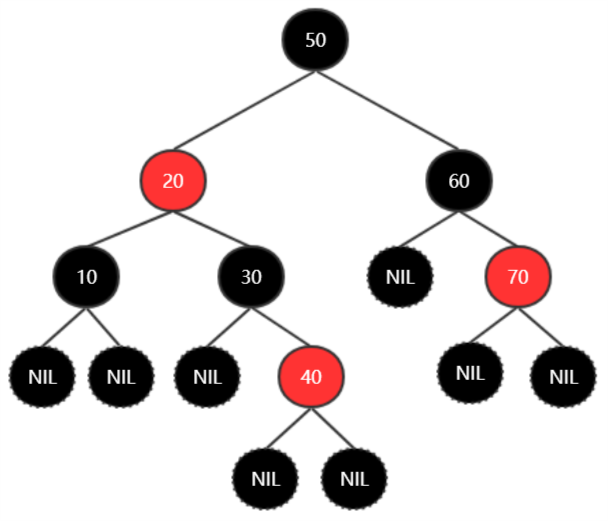
现在我们有一颗红黑树。

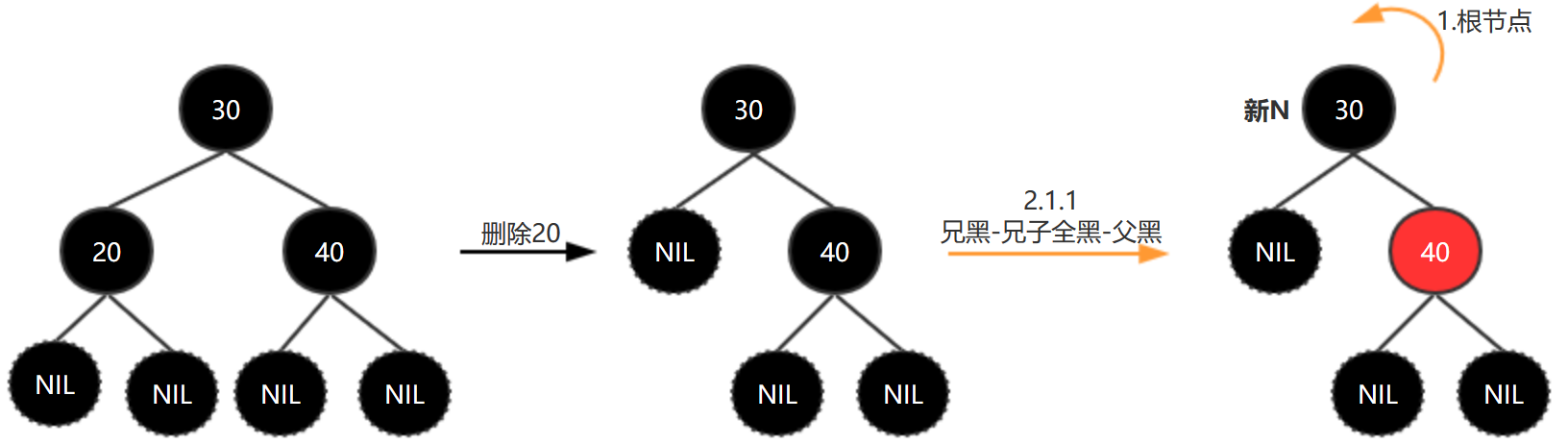
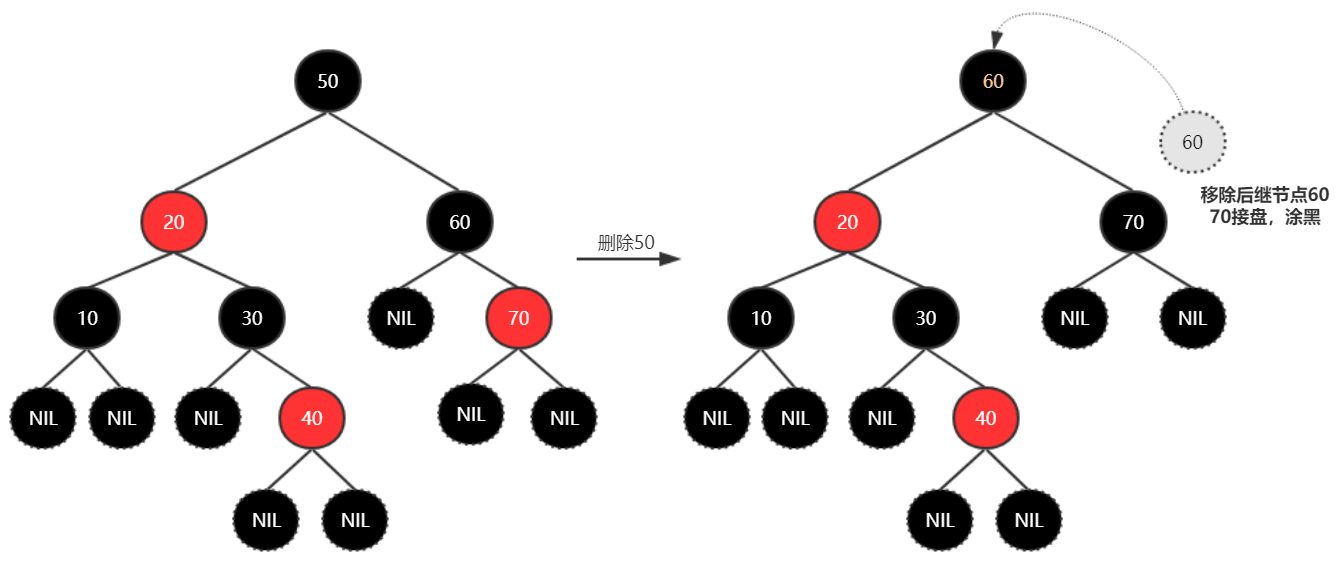
删除50

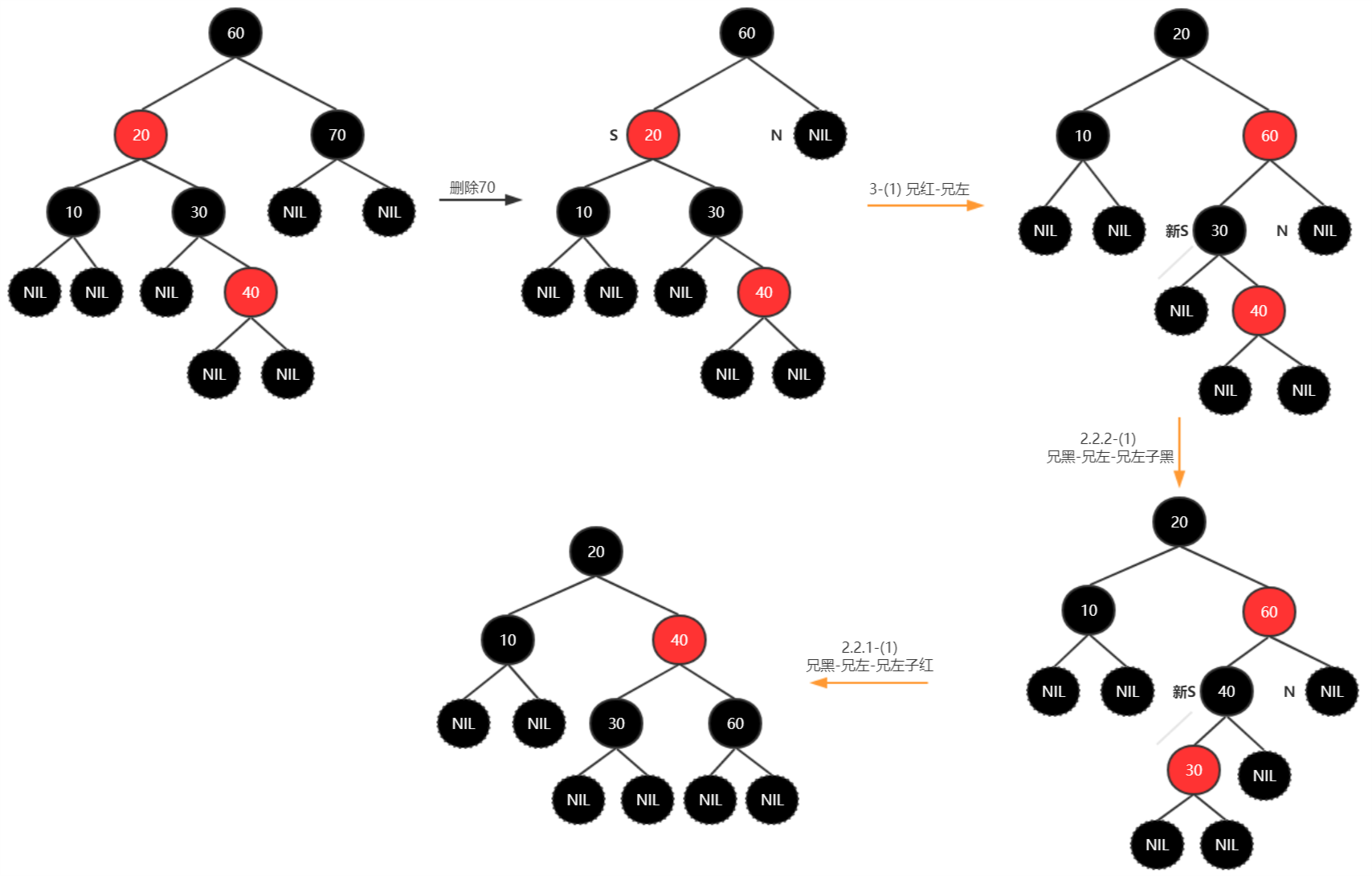
删除70，即黑色叶子节点，进行平衡：

 

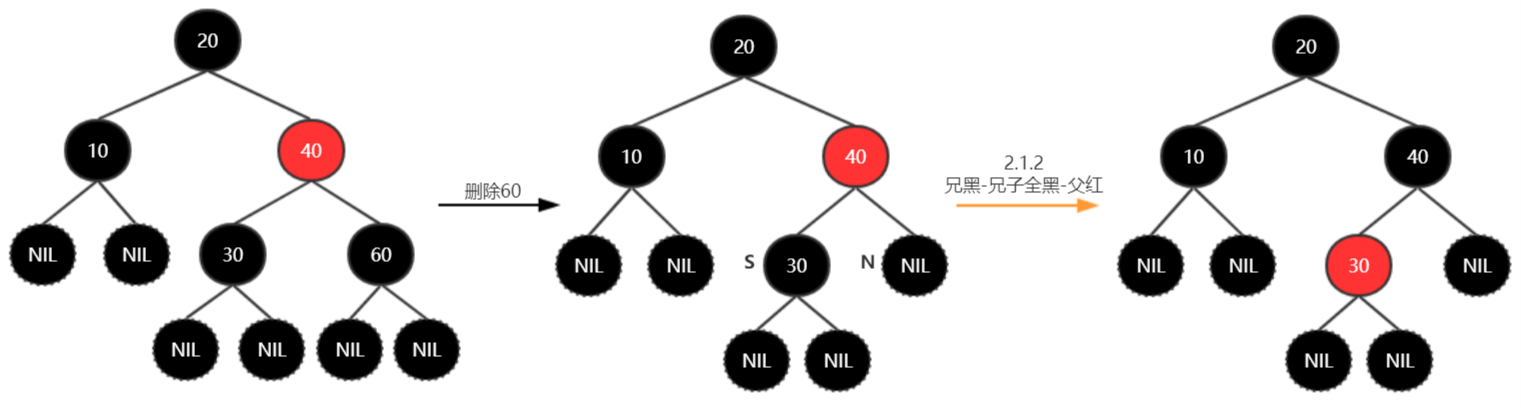
删除60：

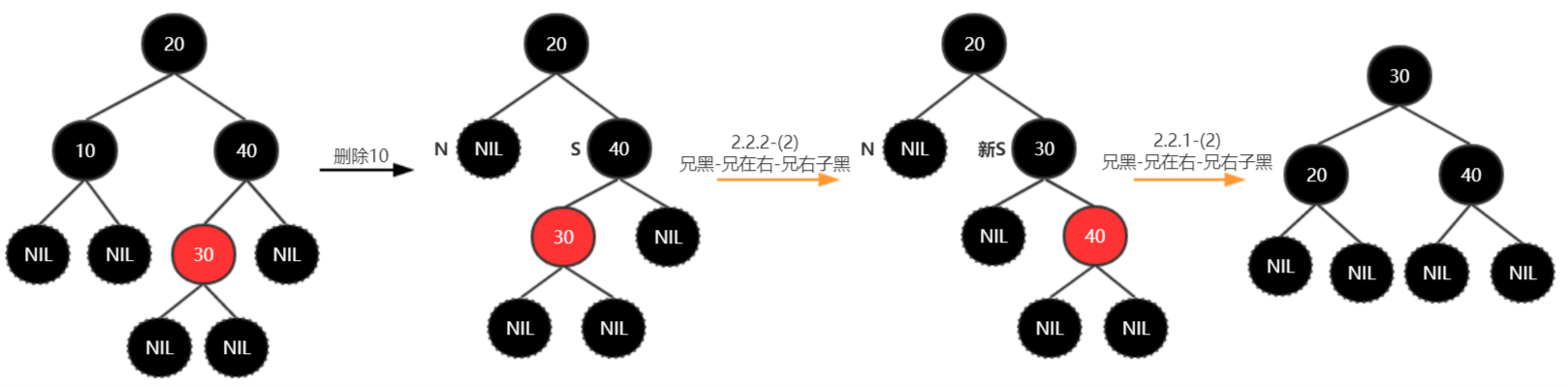
删除10：

删除20