最长公共子序列图解、算法实现和复杂度分析

LCS和莱文斯坦距离的解决思路非常类似，都是利用动态规划的方式来解决。可以参见上一篇“莱文斯坦距离”，两个概念对比着看理解为更深入！

 

LCS定义

同样引用百科：

最长公共子序列（LCS）是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题。与查找最长公共子串的问题不同的地方是：子序列不需要在原序列中占用连续的位置。最长公共子序列问题是一个经典的计算机科学问题，也是数据比较程序，比如Diff工具，和生物信息学应用的基础。它也被广泛地应用在版本控制，比如Git用来调和文件之间的改变。

 

状态转移方程

如果产出的是最长公共子序列的长度，则方程为：

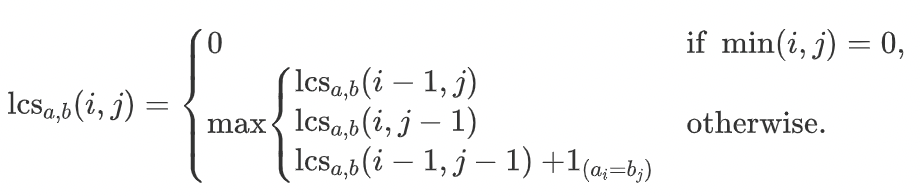
 注意：上面状态转移方程中，最后的1是一个指示函数，表示如果a字符串第i个字符和b字符串第j个字符相同则为1，否则取0；

 

如果最终需要产出最长公共子序列的具体内容，则可以在动态规划的每一步骤保存当前LCS字符串，则最后一步产出的就是两个输入字符串的LCS。对应的状态转移方程也要适当变一下：

1. min(i, j) == 0时，lcs的取值从0改为空字符串；

2. 最后一行指示函数的值从1改为a_i字符的内容。如下所示：

 

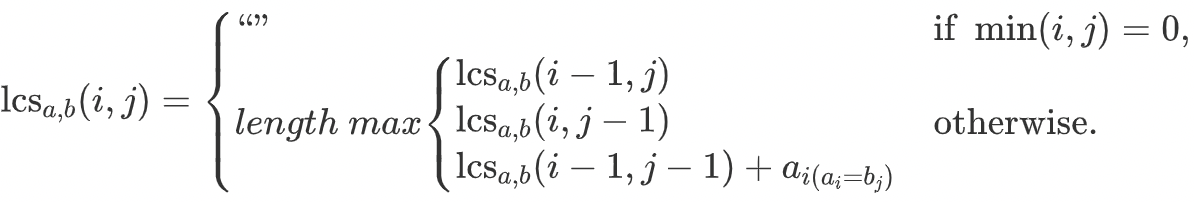
计算过程图解

假设要计算str_a = "abcdd" 和 str_b = "aacbd" 的最长公共子序列，则可以横向从左向右遍历（方便起见，单元格里记录的是lcs的长度，放lcs字符串的话写不下。。）：

如图所示，按照状态转移方程，除了第一行和第一列之外的每个单元格，都只依赖其左、上、左上三个单元格的内容，所以每一行的计算只需要缓存当前横行和上一横行的内容即可。

 

代码实现 

python实现代码如下： 

#-*- encoding:utf-8 -*-
import sys
import pdb


def lcs(str_a, str_b):
    """最长公共子序列
    attributes:
        str_a: 字符串a
        str_b: 字符串b
    return:
        两个字符串的最长公共子序列内容
    exception:
        TypeError
    """

    # 异常检测
    if not isinstance(str_a, basestring) or not isinstance(str_b, basestring):
        raise TypeError("Input must be string!")

    # 定义lcs记录矩阵
    matrix = [["" for j in range(len(str_b) + 1)] for i in range(len(str_a) + 1)]
    
    for i in range(1, len(str_a) + 1):
        for j in range(1, len(str_b) + 1):
            sub_a = matrix[i - 1][j] # 上方单元格
            sub_b = matrix[i][j - 1] # 左侧单元格
            sub_a_b = matrix[i - 1][j - 1] \
                + (str_a[i - 1] if str_a[i - 1] == str_b[j - 1] else "") # 左上单元格

            # 记录下最长的字符串
            tmp_str = sub_a if len(sub_a) > len(sub_b) else sub_b
            matrix[i][j] = tmp_str if len(tmp_str) > len(sub_a_b) else sub_a_b

    return matrix[-1][-1]


def main(str_a, str_b):
    ret = lcs(str_a, str_b)
    print("lcs=%s, lcs_length=%s" % (ret, len(ret)))


if __name__ == '__main__':
    main(sys.argv[1], sys.argv[2])

执行结果

[work@yq01-kg-saa-dev-general0.yq01.baidu.com longest_common_subsequence]$ python lcs_dp.py abcde acdebbbbbb
lcs=acde, lcs_length=4

空间复杂度优化后的代码。优化点有两个：

1. 只创建一个2行的记录矩阵，节省空间；

2. 记录矩阵的列选取相对短的字符串的长度

#-*- encoding:utf-8 -*-
import sys
import pdb


def lcs(str_a, str_b):
    """最长公共子序列
    attributes:
        str_a: 字符串a
        str_b: 字符串b
    return:
        两个字符串的最长公共子序列内容
    exception:
        TypeError: 输入的不是字符串
    """

    # 异常检测
    if not isinstance(str_a, basestring) or not isinstance(str_b, basestring):
        raise TypeError("Input must be string!")

    # 让str_b为更短的字符串，这样空间复杂度能更小一些
    if len(str_a) < len(str_b):
        tmp = str_b
        str_b = str_a
        str_a = tmp

    # 定义一个2 * (len(str_b)+1)的记录矩阵
    matrix = [["" for j in range(len(str_b) + 1)] for i in range(2)]
    curr_i = 1

    for i in range(1, len(str_a) + 1):
        for j in range(1, len(str_b) + 1):
            sub_a = matrix[1 - curr_i][j]
            sub_b = matrix[curr_i][j - 1]
            sub_a_b = matrix[1 - curr_i][j - 1] \
                + (str_a[i - 1] if str_a[i - 1] == str_b[j - 1] else "")

            # 记录下最长的字符串
            tmp_str = sub_a if len(sub_a) > len(sub_b) else sub_b
            matrix[curr_i][j] = tmp_str if len(tmp_str) > len(sub_a_b) else sub_a_b
        curr_i = 1 - curr_i

    return matrix[1 - curr_i][-1]


def main(str_a, str_b):
    ret = lcs(str_a, str_b)
    print("lcs=%s, lcs_length=%s" % (ret, len(ret)))


if __name__ == '__main__':
    main(sys.argv[1], sys.argv[2])

执行结果

$ python lcs_dp_opt.py abcde acdeb
lcs=acde, lcs_length=4

 

复杂度分析

类比莱文斯坦距离的复杂度：

1.  LCS的时间复杂度是O(m * n)

2. LCS的空间复杂度也是O(m * n)，但同样也可以优化成O(2 * min(m, n))，即可以达到O(n)级别