斯坦福【概率与统计】课程笔记（一）：概述
斯坦福【概率与统计】课程笔记（一）
一、概述
课程是把统计和概率分开论述的：先介绍“统计”，然后引出“概率”的概念。
一句话概括“统计”的意义：将数据转变为有用的信息（converting data into useful information），其本质上就是个：搜集数据（Collect data）、汇总数据（Summarize data）和解析数据（Interpret data）的过程。
进一步理解，所谓“统计”，就一定要有一个（我们对之进行研究、学习的）对象集合，课程中将其称为population（注意不仅仅指人口，还泛指动物、物体等，可以引申为就是待处理的数据集合），课程列举了几个可以作为population的例子：
- 美国成人对于死刑的态度
- 小鼠群体对某种化学物质的反应
- 某城市所有单间公寓的平均价格
我们自己也可以列举出类似的无限多的例子：中国境内东北虎的数量、北京市的肺部疾病的发生比例、近10年内全球平均气温变化情况……
所以，我们一般都会用一个圆来表示population：
统计第一步：一般来说，population都会非常大，大到我们无法直接对其展开研究。比如对于“美国成人对于死刑的态度”，你不可能直接去问每一个美国人，那样做成本太高了。实际上更加可行的方案就是抽样（sample）啦。也就是用某种方法，从population中抽取一个小得多的子集（sample）出来，然后基于这个子集做进一步的研究和分析。这就是统计的第一步：数据生成（producing data）。
需要注意的是，上述抽样出来的数据（sample），需要能够完全代表整体数据集合（population），什么意思呢？比如“美国人对于死刑的态度”这个问题，如果你抽样出来的人都是民主党人，那么你将得到“美国人反对死刑”的结论；反之，如果抽样出来的人都是共和党人，那么结论将是“美国人赞同死刑”（美国多数民主党人反对死刑，而多数共和党人是赞同死刑的）。你看，因为抽样不准确的原因，导致了最终得到完全相反的结果。这就叫做“抽样有偏”，即抽样出来的数据不能很好地代表整体数据集合的分布情况。反过来说，一个好的抽样数据子集合，其在民主党和共和党人数的比例上，与美国整体民主党与共和党人数的分布比例应该是一样的（当然这只是一个维度，还有其他的维度比如性别分布、年龄分布、受教育程度、收入情况等等，抽样的数据都应该和整体数据集合一致，这才是一个“好”的抽样子集合）。但事实上，我们是无法做到抽样数据和整体数据百分之百同分布的，因为现实中总是会有各种误差和偏差的。
统计第二步：现在我们拿到了抽样数据，一般来说，我们会拿到一份类似于问答清单或数据列表之类的东西。想象一下，你针对“美国人对死刑的态度”这个问题进行抽样调查，你会针对抽样人群发放一个调查问卷，其中包括各种问题如年龄、教育水平、收入层次、党派、对死刑的态度、对终身监禁的态度的答案。下面要做的就是基于这份数据进行各种汇总、组织的工作，将其变为一份“有价值”的数据了。这个过程叫做数据探索分析（exploratory data analysis）。
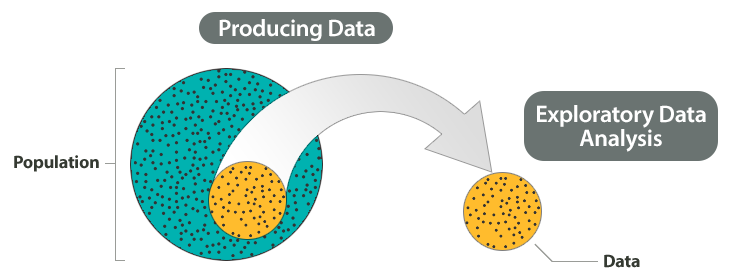
有读者会问：我不是只想知道态度嘛？直接汇总大家对死刑态度的数据不就得了，干吗还要分析其他信息呀？我的理解是，一般来说我们做一项数据分析调查，除了想得到直接答案的分布，还想要得到导致这个答案分布的原因等等信息（比如性别、党派、受教育程度不同的人群对于死刑态度有没有区别），这样才能得到一个比较完整全面的结论支撑。
统计第三步：现在我们有了一个基于抽样数据的分析结论，而我们根本的目的是要得到基于全集（population）的结论。那么我们能否将基于抽样的结论直接作为全集的分析结论呢？正如上面提到的，现实中总会有各种误差、偏差，所以抽样总会是有偏的。这就导致我们无法直接将抽样分析结论作为整体分析结论，而是要加一个diff分析和纠正的动作，这个过程被称为概率化（probability）。
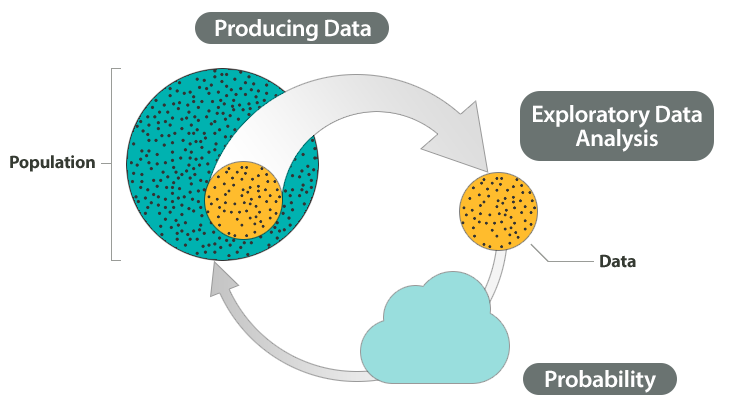
统计第四步：基于抽样分析及将其概率化之后的结论，我们将其迁移到整体数据上，作为整体数据集合的分析结论。这个过程叫推断（inference）。
上面最后这一张图，就是课程对于“统计”的整体理解，注意一共有四个步骤：数据生成(同分布抽取)、数据探索分析(汇总、组织）、概率化(分析抽样数据偏差并纠正)、推断(将抽样结论同步到整体数据集合）。
课程还给了一个例子说明上述四个步骤：
1. 数据生成：比如同分布抽样了1085名美国人作为样本，咨询他们对于死刑的态度（赞成或反对）；
2. 数据探索分析：经过数据分析、组织和汇总，得出1085人种，65%支持对于犯谋杀罪的嫌疑人执行死刑；
3. 概率化和推断：在上述结论的基础上，结合先验知识：有95%的置信度，确信全体美国人的答案对比上面结论，有3%以内的误差，即全体美国人中赞同死刑的比例大概在62%到68%之间。
概述到此结束。
未完待续……
