字符串模式匹配算法系列(二):KMP算法
算法背景:
KMP算法是由Donald Knuth和Vaughan Pratt于1970年共同提出的,而James H.Morris也几乎同时间独立提出了这个算法。因此人们将其称作“克努特-莫里斯-普拉特”算法(简称KMP)。
KMP算法的学习,可以在掌握了BF算法原理、并结合“BF算法效率低”作为切入点来理解,这样感觉比较符合大家的思维习惯。
算法原理:
上一篇博文《BF算法》的最后,有提到BF算法每次发现不匹配时,目标字符串只能向后挪动一个字符的距离,隐约感觉这样效率很低。
所以自然想到:发现不匹配时,目标字符串能不能向后多挪动几个字符的距离、从而加快整个算法的速度?甚至说极端一些,直接把目标字符串挪动到不匹配的位置上然后继续呢?

![]()

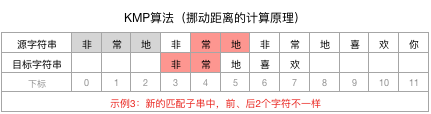
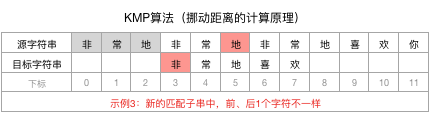
观察上面两张图,可以发现,向后挪动太多了是不行的,这样可能错过了原本可以匹配的基准点:
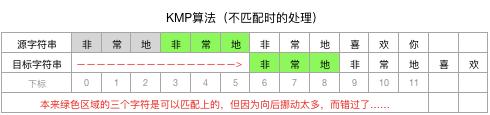
小结一下:
BF算法,是把目标字符串向后挪动一个字符(第一轮在下标0的位置上,第二轮挪到下标1、第三轮挪到下标2、第四轮挪到下标3并匹配成功),这样可以确保不会错过可以匹配的基准点,但效率太低;
我们的新想法,是把目标字符串向后多挪动几个字符,但不确定应该挪动几个字符,如果挪多了,就会错过潜在可以匹配的基准点(就像上面说的极端情况:一次向后挪动了6个位置,结果错过了下标3的那个可以匹配的基准点)
既想把目标字符串向后多挪动几个字符、从而加快速度,但又不能因为挪动的太快太多、而错过了原本可以匹配的字符。怎样才能同时做到这两点?
KMP算法,就是预先计算好这个应该挪动的字符数,这样问题就迎刃而解:即加快了向后挪动目标字符串的距离,又确保不会错过可能匹配的基准点。
我们仍然借用整个算法的执行过程,来说明“应该挪动的字符数”是如何确定的,然后再说明其是可以提前计算好的。
假定现在的不匹配点在下标6的位置,因此要计算目标字符串前面的字符串“非常地非常地”的最大向后挪动距离。

首先可以看到,下标6前面的字符串是“非常地非常地”,这个字符串在源字符串和目标字符串里是一样的(肯定是一样的,不然也不会到下标6才发现不匹配……),我们将其称作匹配子串。
仔细想一下:此时目标字符串向后挪动一段“恰当”的距离,是因为:挪动后的目标字符串中的匹配子串的前n个字符,与源字符串中的匹配子串的后n个字符有可能会匹配上。
因为我们不能错过这个潜在的匹配,所以才不能像前文说的那样,一次挪动的太多:

将上面两段描述综合起来看,其实就是在寻找:不匹配点前面的匹配子串的相同且最长的前n个字符和后n个字符,我们来实际演示一下寻找过程:



综上,下标6的这个不匹配点,它的匹配子串“非常地非常地”的长度为6,其前3个字符和后3个字符一样,即n=3
所以目标字符串可以向后挪动的距离就是6-3=3个位置(到下标3),这样就加快了挪动速度,又不会错过潜在的匹配基准点。

为了巩固说明,再举一个类似的例子,我们换一个目标字符串为:“非常地喜欢”,则现在不匹配点是在下标3的位置:
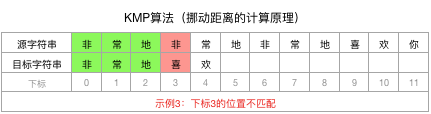
拿到下标3前面的字符串“非常地”,计算其相同且最长的前n个字符和后n个字符
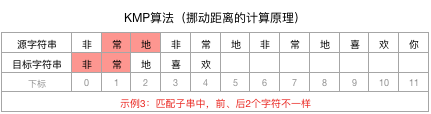
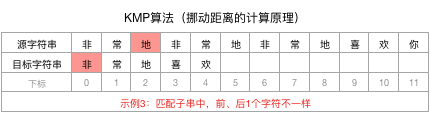
进而得到结论,“非常地”没有相同的前、后n个字符,即n=0。
匹配子串的长尾为3,其中没有相同的前后n个字符(n为0),所以就可以直接让目标字符串向后移动3-0=3个位置,并开始新一轮匹配:

类似地,匹配子串长尾是3,相同且最长的前后n个字符没有找到,即n=0,所以目标字符串可以再向后移动3-0=3个字符,并开始新一轮匹配:

最终匹配成功。
从上面的例子可以看到几个现象:
1. “可以向后挪动的距离” = 位置 - 最长且相同的前/后缀子串
2. 在实际执行匹配算法之前,1可以只依靠目标字符串得到
3. 在实际使用算法之前无法知道具体在哪个位置不匹配,所以只能假设目标字符串每个位置都可能不匹配,并将不匹配点前面部分作为匹配子串来计算“相同且最长的前、后n个字符”,进而结合当前位置,得到这个不匹配点上可以向后挪动的距离。
进一步,可以将每个位置的【配置子串中最长且相同的前/后缀串】存储成为一个备份表,在实际算法执行时,根据目标字符串不匹配的实际位置,直接查询这张备份表,两者相减就可以得到此时此刻向后挪动的距离。这张备份表的学名就是【部分匹配表】
举个例子,如果目标字符串为“非常地非常地喜欢”,则其【部分匹配表】的内容为:
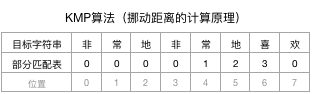
强调一下:部分匹配表中每一列的部分匹配表的值,是以其前面的子串来计算的。例如:位置6的“喜”字,其部分匹配表的值(3),是根据其前面的匹配子串“非常地非常地”计算来的,而不是“非常地非常地喜”(即不包括本身)!
实际使用时,用对应的位置值 - 备份表的值,就是目标字符串可以向后移动的距离。例如:位置6不匹配了,其目标字符串可以向挪动:6-3=3个位置。如果位置7不匹配了,目标字符串可以向后挪动7-0=7个位置。
类似地,如果目标字符串为“非常地喜欢”,则其部分匹配表的内容为:
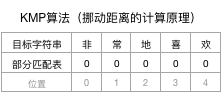
这张部分匹配表所有值都是0,说明任何位置不匹配都可以直接跳到不匹配点重新比较,这种情况无疑是速度最快的情况。
由此也可以看出,目标字符串里前后重复的字符越少,目标字符串向后挪动的速度就越快,整个算法的效率就越高。
下面介绍一下【部分匹配表】的计算过程。
(此处稍后补充)
算法实现
KMP的python实现如下:
1 #!/usr/bin/env python 2 #-*- coding: utf-8 -*- 3 import sys 4 5 reload(sys) 6 sys.setdefaultencoding('utf-8') 7 8 9 class KMP(object): 10 """KMP算法 11 成员变量: 12 s: 源字符串 13 t: 目标字符串 14 pmt: 部分匹配表(向右挪动了1格, 位置0赋-1) 15 """ 16 def __init__(self, s, t): 17 self.s = s 18 self.t = t 19 self.pmt = {} 20 21 def _get_pmt_1(self): 22 """根据目标字符串,计算前后缀的最大重复子串 23 此方法简单,但dn指针可能回退到-1,且up不是每次都递增,所以while循环次数最多可能是t长度的两倍 24 """ 25 self.pmt[0] = -1 # 位置0赋值-1,为了计算方便 26 up = 0 # up表示上指针,用来向后移动从而实现错位 27 dn = -1 # dn表示下指针,用来记录匹配的位置 28 29 while up < len(self.t): 30 if dn == -1 or self.t[up] == self.t[dn]: 31 up += 1 32 dn += 1 33 self.pmt[up] = dn 34 else: 35 dn = self.pmt[dn] 36 37 def _get_pmt_2(self): 38 """根据目标字符串,计算前后缀的最大重复子串 39 此方法略复杂,但dn指针不后退且up每次都递增1,所以while循环次数为t的长度 40 """ 41 self.pmt[0] = -1 # 位置0赋值-1,为了计算方便 42 self.pmt[1] = 0 # 位置1赋值0,表示没有匹配 43 up = 1 # up表示上指针,用来向后移动从而实现错位 44 dn = 0 # dn表示下指针,用来记录匹配的位置 45 same_len = 0 # 表示匹配的字符串长度 46 47 while up < len(self.t): 48 if self.t[up] == self.t[dn]: 49 dn += 1 50 same_len += 1 51 else: 52 same_len = 0 53 up += 1 54 self.pmt[up] = same_len 55 56 def run_1(self): 57 """完全匹配则返回源字符串匹配成功的起始点的下标,否则返回-1 58 此方法简单,但循环次数比run_2多一倍 59 """ 60 ptr_s = 0 61 ptr_t = 0 62 63 # 获取pmt 64 self._get_pmt_1() #也可以用self._get_pmt_2() 65 66 while ptr_t == -1 or ptr_s < len(self.s) and ptr_t < len(self.t): 67 if self.s[ptr_s] == self.t[ptr_t]: 68 ptr_s += 1 69 ptr_t += 1 70 else: 71 ptr_t = self.pmt[ptr_t] 72 73 if ptr_t == len(self.t): 74 return ptr_s - ptr_t 75 return -1 76 77 def run_2(self): 78 """完全匹配则返回源字符串匹配成功的起始点的下标,否则返回-1 79 此方法复杂,但循环次数比run_1少一半 80 """ 81 base = 0 82 same_len = 0 83 len_s = len(str_s) 84 len_t = len(str_t) 85 86 # 获取pmt 87 self._get_pmt_2() #也可以用self._get_pmt_1() 88 89 while base + len_t <= len_s: 90 step = 0 91 while step + same_len < len_t: 92 if self.t[step + same_len] == self.s[base + step + same_len]: 93 # 当前字符相同,则继续比较下一个字符 94 step += 1 95 continue 96 # 当前字符不相同,则结束次轮比较,更新base基准位置,启动下一轮比较 97 same_len = self.pmt[step] 98 base += step - same_len 99 break 100 # 完全匹配成功,算法结论,返回匹配成功的基准点位置下标 101 if step + same_len == len_t: 102 return base 103 # 遍历了所有情况,最终匹配失败,返回-1 104 return -1 105 106 107 if __name__ == '__main__': 108 str_s = u"非常地非常地非常地喜欢你" 109 str_t = u"非常地喜欢" 110 model = KMP(str_s, str_t) 111 print model.run_2()
算法评估
假设源字符串长度为m,目标字符串长度为n
KMP的时间复杂度为O(m+n)
KMP的空间复杂度为O(n),因为多了一个和目标字符串相同长度的备份表




