[LeetCode] 309. Best Time to Buy and Sell Stock with Cooldown(买卖股票的最佳时机(带 CD 版))
-
Difficulty: Medium
-
Related Topics: Dynamic Programming
-
Link: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/
Description
Say you have an array for which the ith element is the price of a given stock on day i.
你有一个数组,第 i 个元素表示某只股票在第 i 天的售价
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
设计一个算法寻找这支股票的最大收益。你可以进行任意次交易(每次买卖 1 股,可进行多次),但需遵循以下限制:
- You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
你不能在同一天内进行多次交易(也就是说,你必须在买进下一股前把你的上一股卖出)。 - After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
当你卖出股票后,第二天你不能买入股票。(也就是说,有 1 天的 CD)
Example
Input: [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]
Solution
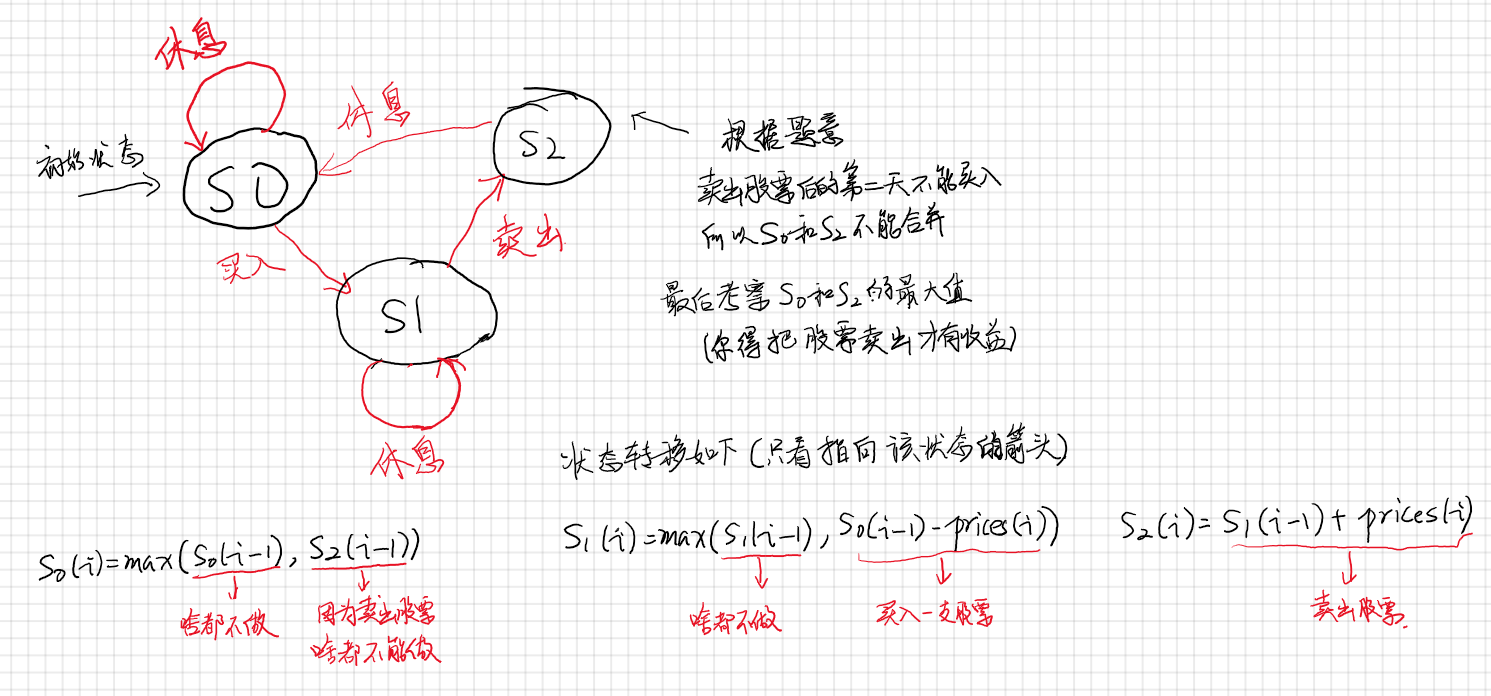
一开始没有啥思路,看到 discussion 里一个“基于状态机的 DP”后大概理解怎么做了,具体解法看下图(字渣见谅),代码如下:
import kotlin.math.max
class Solution {
fun maxProfit(prices: IntArray): Int {
val s0 = IntArray(prices.size)
val s1 = IntArray(prices.size)
val s2 = IntArray(prices.size)
s0[0] = 0
// 第 0 天买入股票
s1[0] = -prices[0]
// 第 0 天无法卖出,给个最小值吧
s2[0] = Int.MIN_VALUE
for (i in 1..prices.lastIndex) {
s0[i] = max(s0[i - 1], s2[i - 1])
s1[i] = max(s1[i - 1], s0[i - 1] - prices[i])
s2[i] = s1[i - 1] + prices[i]
}
return max(s0.last(), s2.last())
}
}


