[LeetCode] 11. Container with Most Water（盛水量最多的容器）

• Difficulty: Medium

• Related Topics: Array, Two Pointers

• Link: https://leetcode.com/problems/container-with-most-water/

Description

Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0). Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.
给定 n 个非负整数 a1, a2, ..., an，每一个整数表示一个坐标 (i, ai)。绘制了 n 条垂线段，每条垂线段的两端点坐标分别为 (i, ai) 和 (i, 0)。寻找到两条线，以这两条线加上 x 轴所构成的容器的盛水量最多。

Notice that you may not slant the container.
注意你不能倾斜容器。

Examples

Example 1

Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2

Input: height = [1,1]
Output: 1

Example 3

Input: height = [4,3,2,1,4]
Output: 16

Example 4

Input: height = [1,2,1]
Output: 2

Constraints

• n = height.length

• 2 <= n <= 3 * 10^4

• 0 <= height[i] <= 3 * 10^4

Hints

1. The aim is to maximize the area formed between the vertical lines. The area of any container is calculated using the shorter line as length and the distance between the lines as the width of the rectangle.
   本题的目标是使两条垂线间组成的面积最大化。任意容器的面积都可以通过两条垂线中较短的那条的长度以及这两条线之间的距离计算

   Area = length of shorter vertical line * distance between lines
面积 = 两条垂线中较短的那条的长度 * 两条线之间的距离

   We can definitely get the maximum width container as the outermost lines have the maximum distance between them. However, this container might not be the maximum in size as one of the vertical lines of this container could be really short.
   我们可以轻易得知，最宽的容器一定是最外围两条垂线之间构成的容器。然而，这个容器并不一定是面积最大的，因为两条垂线中的一条可以非常短。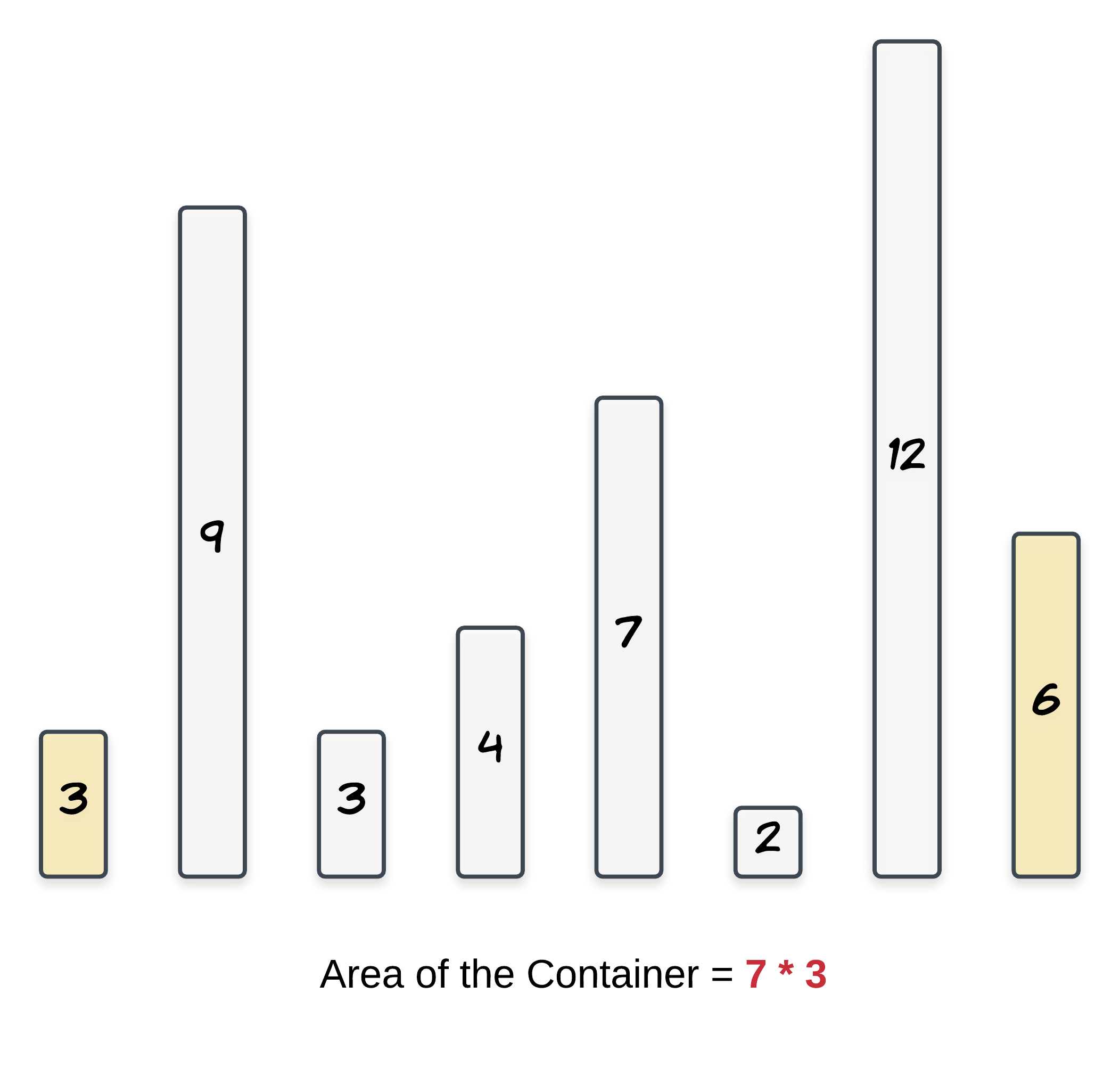

   

   

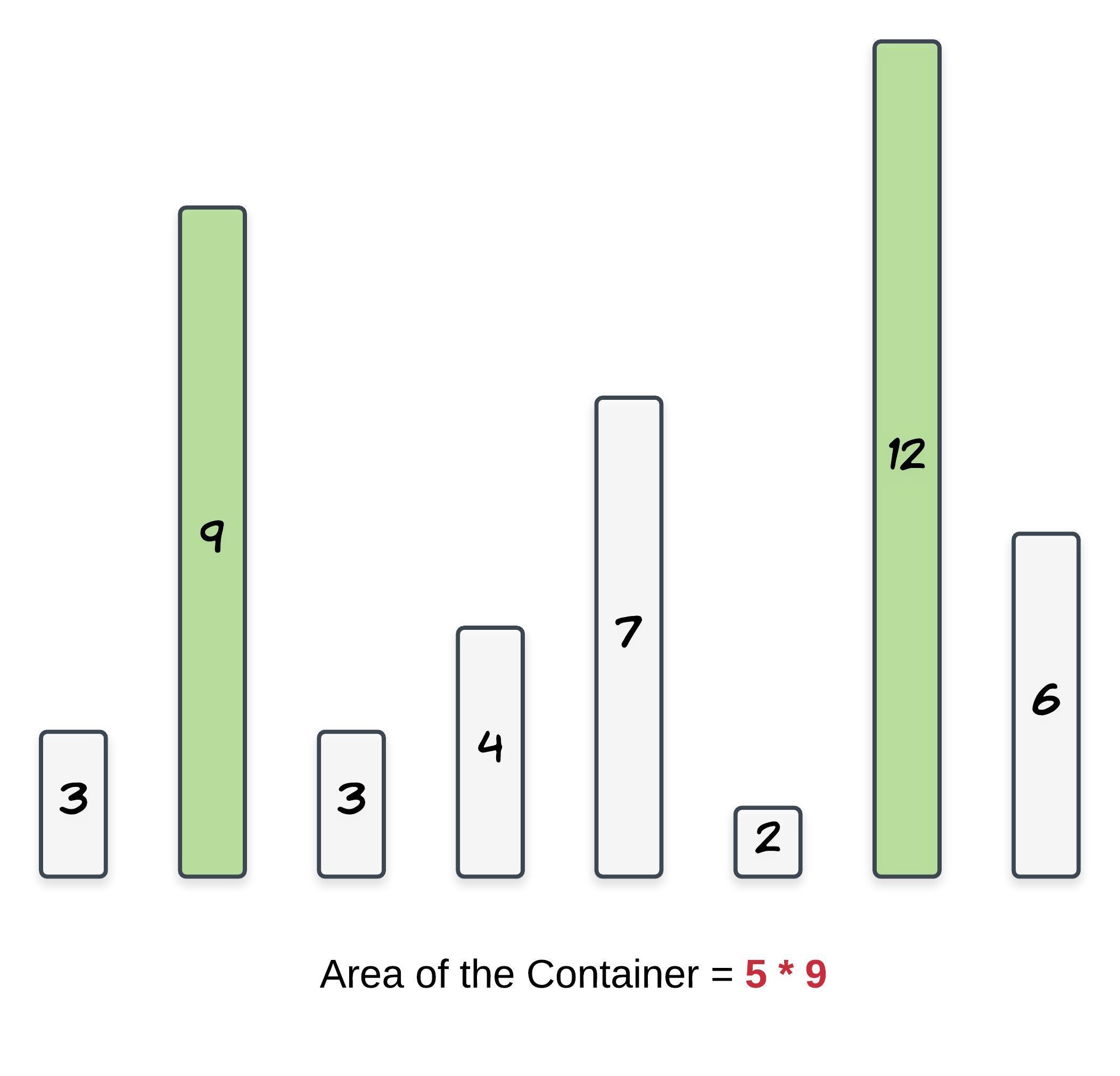
2. Start with the maximum width container and go to a shorter width container if there is a vertical line longer than the current containers shorter line. This way we are compromising on the width but we are looking forward to a longer length container.
   从最宽的容器开始，如果内侧容器里有比外侧容器中较短边长的边，则将容器往内缩。通过这种方式，我们在宽度上有所牺牲，但我们可以找到更高的容器。

Solution

提示已经给出了一个比较明显的解答了，照着提示的思路即可，代码如下：

import kotlin.math.max
import kotlin.math.min

class Solution {
    fun maxArea(height: IntArray): Int {
        var left = 0
        var right = height.lastIndex
        var maxArea = -1

        while (left in 0 until right && right <= height.lastIndex) {
            maxArea = max(maxArea, min(height[left], height[right]) * (right - left))
            // 较长边不动，找一个高于较短边的边
            if (height[left] > height[right]) {
                right--
            } else {
                left++
            }
        }
        return maxArea
    }
}