数据结构：第六章学习小结

第六章学习小结

 

一、  学习内容小结

 

 

 

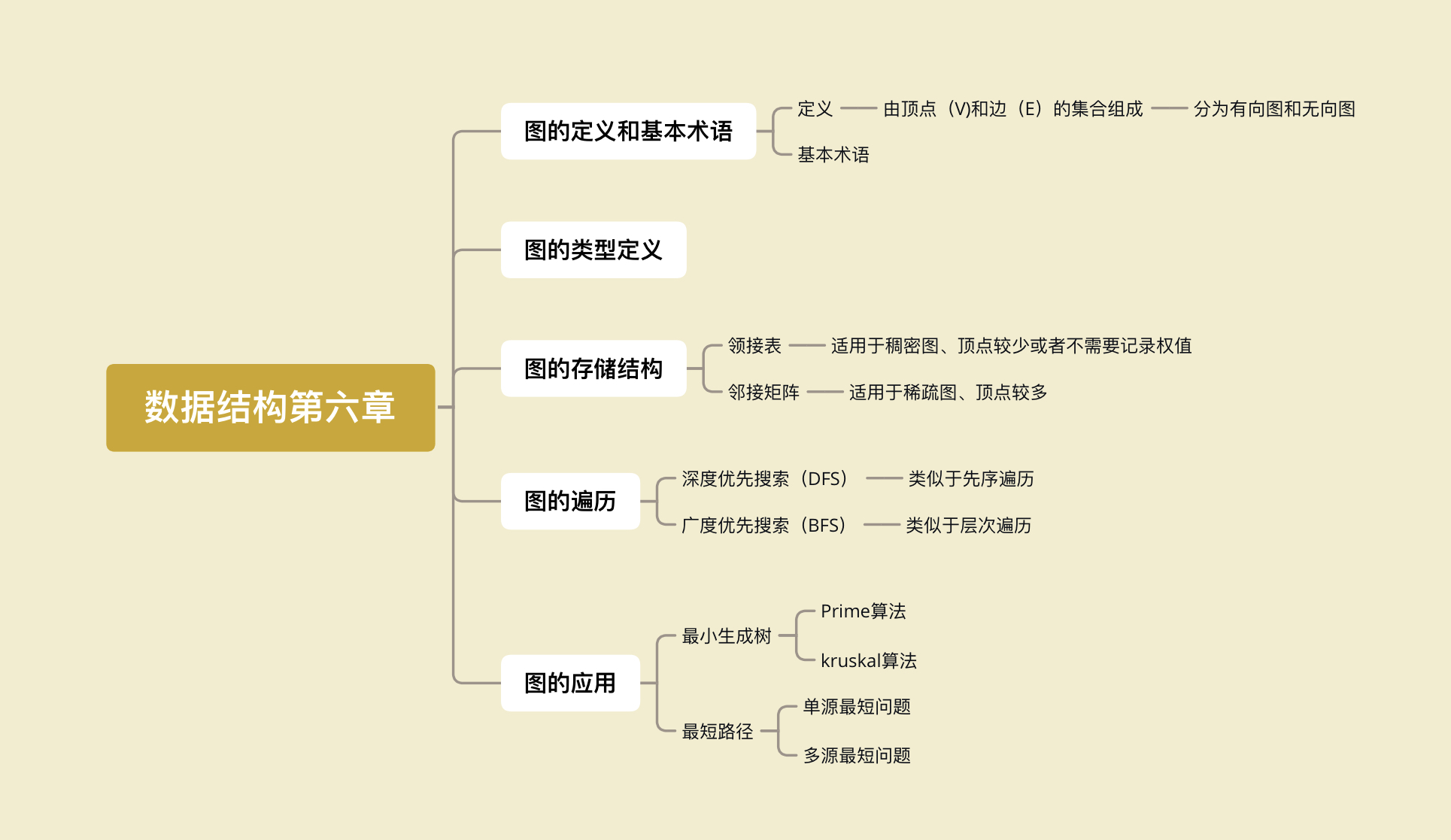
##存储结构

#邻接矩阵：表示顶点之间相邻关系的矩阵

 若没有权值，则有边记录为1，无边记录为0

 若有权值，则有边记录为权值，无边记录为INT_MAX

 需要一个用于存储邻接矩阵的二维数组和一个一维数组来存储顶点信息。

 在图G中查找顶点u：

int LocateVex(AMGraph G, VertexType u)
{//存在返回下标，不存在返回-1
    int i;
    for (i = 0; i < G.vexnum; i++)
    {
        if (u == G.vexs[i])
            return i;
    }
    return -1;
}

优点：1、方便查找是否有边

           2、方便查找任一顶点的所有由边直接相连的顶点

 

#邻接表：链式存储结构

1、表头结点表：包含数据域和链域

2、边表：邻接点域、数据域和链域

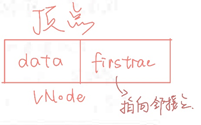
查找顶点所在下标：

int LocateVex(ALGraph G, VerTexType u)
{//搜索顶点u是否存在，存在返回下标，不存在返回-1
    int i;
    for (i = 0; i < G.vexnum; i++)
    {//i要合法
        if (u == G.vertices[i].data)
        {//查找顶点名字
            return i;
        }
    }
    return -1;
}

优点：

1、 便于统计边的数目

2、便于删除和增加

      

##遍历

#深度优先搜索（DFS）：类似于先序遍历

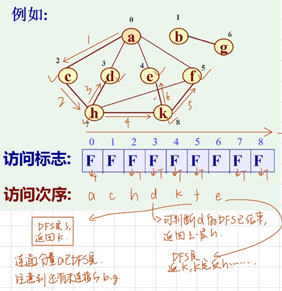
注意到其中的b-g是非连通的，若要访问b-g，则需要在DFS外在打包一层循环

#广度优先搜索（BFS）：类似于层次遍历

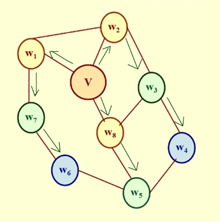如果遇到了非连通图，同理DFS

 ##应用

#最小生成树

最小生成树不是唯一的，但权值一定是相同的

注意不能形成回路

Prime算法：选择顶点

Kruskal算法：选择边

#最短路径

单源最短路径

 

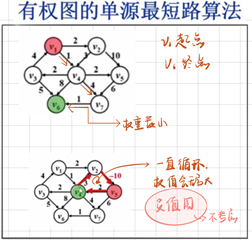
Dijkstra算法：按照递增的顺序找出各个顶点的最短路

 

二、学习体会

    个人感觉这一章的内容的难度比以往都要大，不管是逻辑理解还是代码实现都是如此。在解题的过程中需要非常的小心仔细，一时分心就很容易出现错误（例如在求解最小生成树或最小路径时，若中间一步错了就很容易导致步步错）。其次就是，图转为邻接矩阵和邻接表对于我来说也是一个难点，会发现对着图做题时比较轻松，但是面对领接矩阵或者是邻接表时就很难够去转换成图来思考。

三、目标

    书读的不够透，在完成题目时，发现自己对一些概念上的问题还有不解。希望能够做到提前预习，把书和题都理解透，然后继续提高代码能力。