DS博客作业06--图
1.本周学习总结
1.思维导图
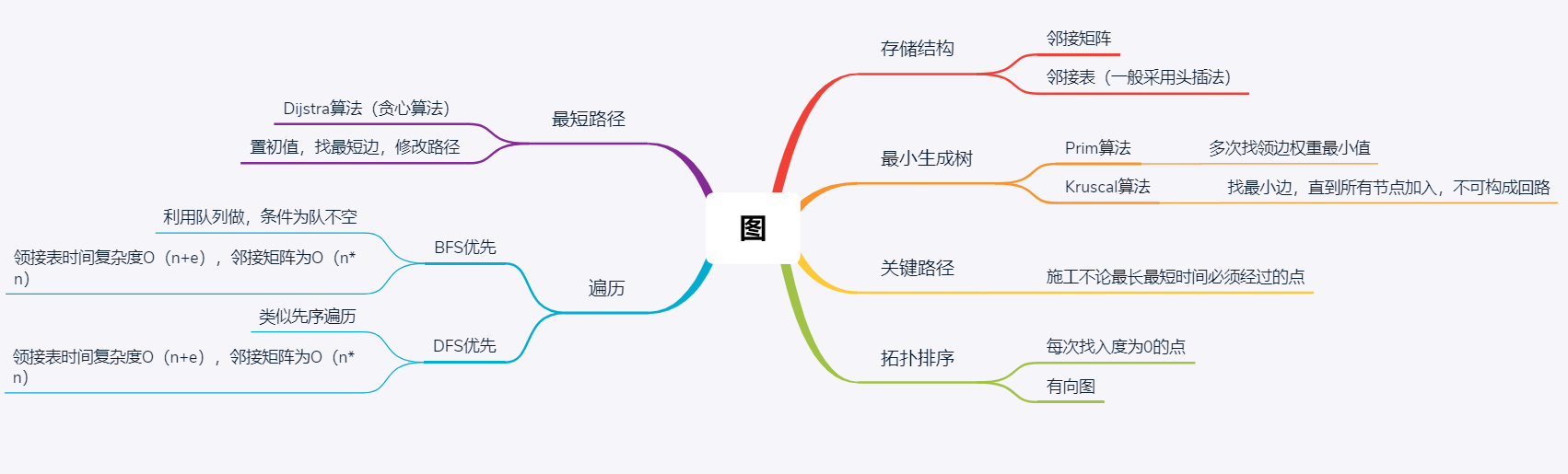
2.谈谈你对图结构的认识及学习体会
对图结构的学习,发现容器超好用,他大大减少了代码量,库函数的调用非常方便。下面是总结的一些常用库函数
1.vector类常用的函数
- vector():创建一个空vector
- vector(begin,end):复制[begin,end)区间内另一个数组的元素到vector中
- void push_back(const T& x):向量尾部增加一个元素X
- iterator insert(iterator it,const T& x):向量中迭代器指向元素前增加一个元素x
- iterator erase(iterator it):删除向量中迭代器指向元素
- void pop_back():删除向量中最后一个元素
- void clear():清空向量中所有元素
2.set容器
- 所有元素都会根据元素的键值自动排序,set元素的键值就是实值,实值就是键值。set不允许两个元素有相同的键值
set成员函数列表如下: - begin()--返回指向第一个元素的迭代器
- clear()--清除所有元素
- empty()--如果集合为空,返回true
- erase()--删除集合中的元素
- find()--返回一个指向被查找到元素的迭代器
- insert()--在集合中插入元素
- size()--集合中元素的数目
3.map容器
map可以同时拥有实值(value)和键值(key),其余用法和set差不多
此次图的学习,感觉好像比树更简单,实际却考的更差。平时自己做题要想好久,等考前考后再去做的时候,思路好像更清晰了,不知是见多不怪还是熟能生巧。做题中发现除非要删除、增加之类的问题,不然还是少用邻接表吧,用的时候超容易出错,邻接矩阵的话,通俗易懂代码量还更少,当然,能熟练使用容器更好了,非常方便。
2.PTA实验作业
2.1.题目1:图着色问题
给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
输入格式:
输入在第一行给出3个整数V(0<V≤500)、E(≥0)和K(0<K≤V),分别是无向图的顶点数、边数、以及颜色数。顶点和颜色都从1到V编号。随后E行,每行给出一条边的两个端点的编号。在图的信息给出之后,
给出了一个正整数N(≤20),是待检查的颜色分配方案的个数。随后N行,每行顺次给出V个顶点的颜色(第i个数字表示第i个顶点的颜色),数字间以空格分隔。题目保证给定的无向图是合法的(即不存在自回路和重边)。
输出格式:
对每种颜色分配方案,如果是图着色问题的一个解则输出Yes,否则输出No,每句占一行。
输入样例:
6 8 3
2 1
1 3
4 6
2 5
2 4
5 4
5 6
3 6
4
1 2 3 3 1 2
4 5 6 6 4 5
1 2 3 4 5 6
2 3 4 2 3 4
输出样例:
Yes
Yes
No
No
2.1.1设计思路
- 定义vector和set容器来做
- 根据输入各店之间的关系来将元素a放在b的后面,b放在a的后面,类似于建链接表的的过程
- 依次输入num组数据
- flag初始化为1
- 每次都需将容器 s 清空
- 依次输入各点对应的颜色,将颜色插入到容器 s 中(此处相同color只记一次)
- 如果容器 s 大小不等于颜色总数k
- flag=0该涂色方案不可行
- 遍历每个节点
- 遍历与该节点相邻的节点
- 如果两相邻节点颜色相同
- 不符合涂色方案,跳出循环
- 如果flag=0不符合,跳出循环
- if(flag=1)输出符合方案
- 否则,输出不符合
2.1.2代码截图
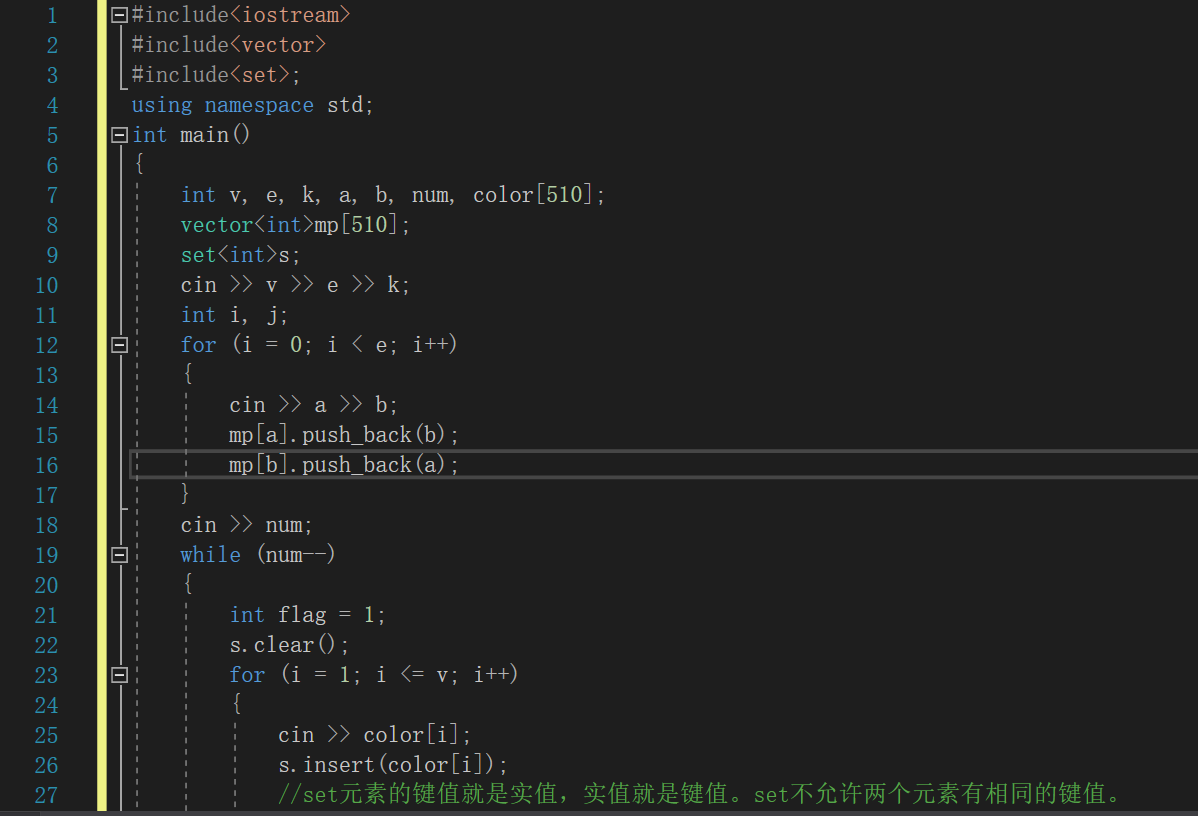
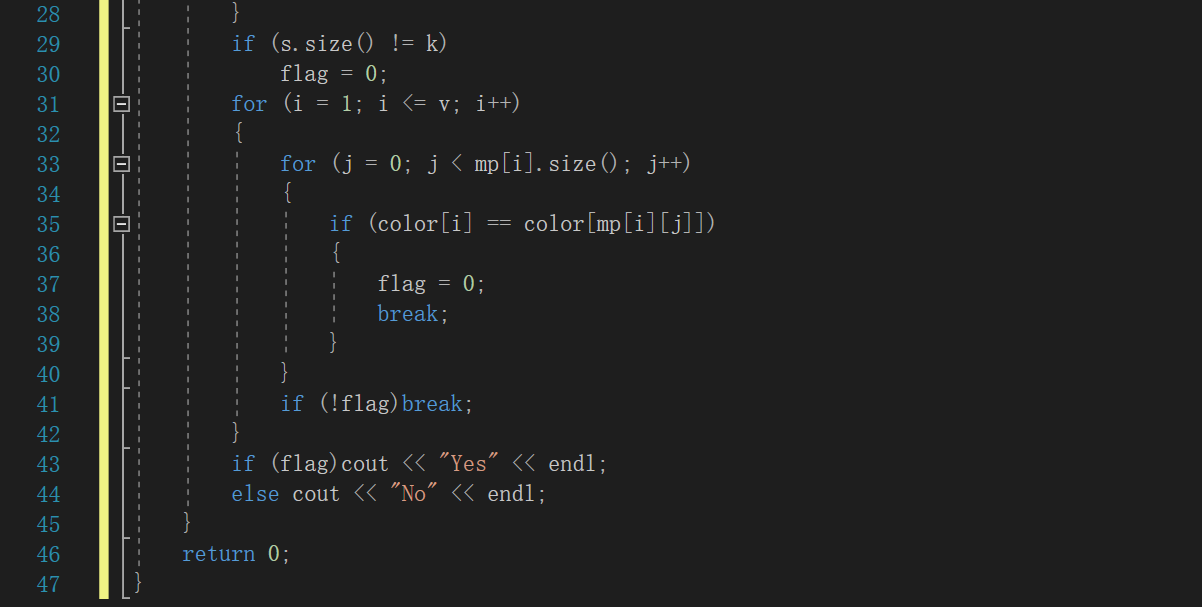
2.1.3本题PTA提交列表说明

- Q1:不知如何将颜色存入节点信息,发现存入data里面待会next又没有data这个类型
- A1:改成邻接矩阵,定义中间变量num[i]存储颜色,并用哈希数组判断颜色种类是否合理
- A2:发现改成容器做更方便,也不用进行建图操作什么的,直接调用函数判断有没有相等,代码量减少一半且方便易懂
2.2 题目2:六度空间
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式:
第1行给出两个正整数,分别表示社交网络图的结点数N(1<N≤10000,表示人数)、边数M(≤33×N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
输出样例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%
2.2.1设计思路
利用广度遍历逐层遍历图,并记录层数
该题和前面函数题广度遍历差不多,同时结合了树的按层来划分思想
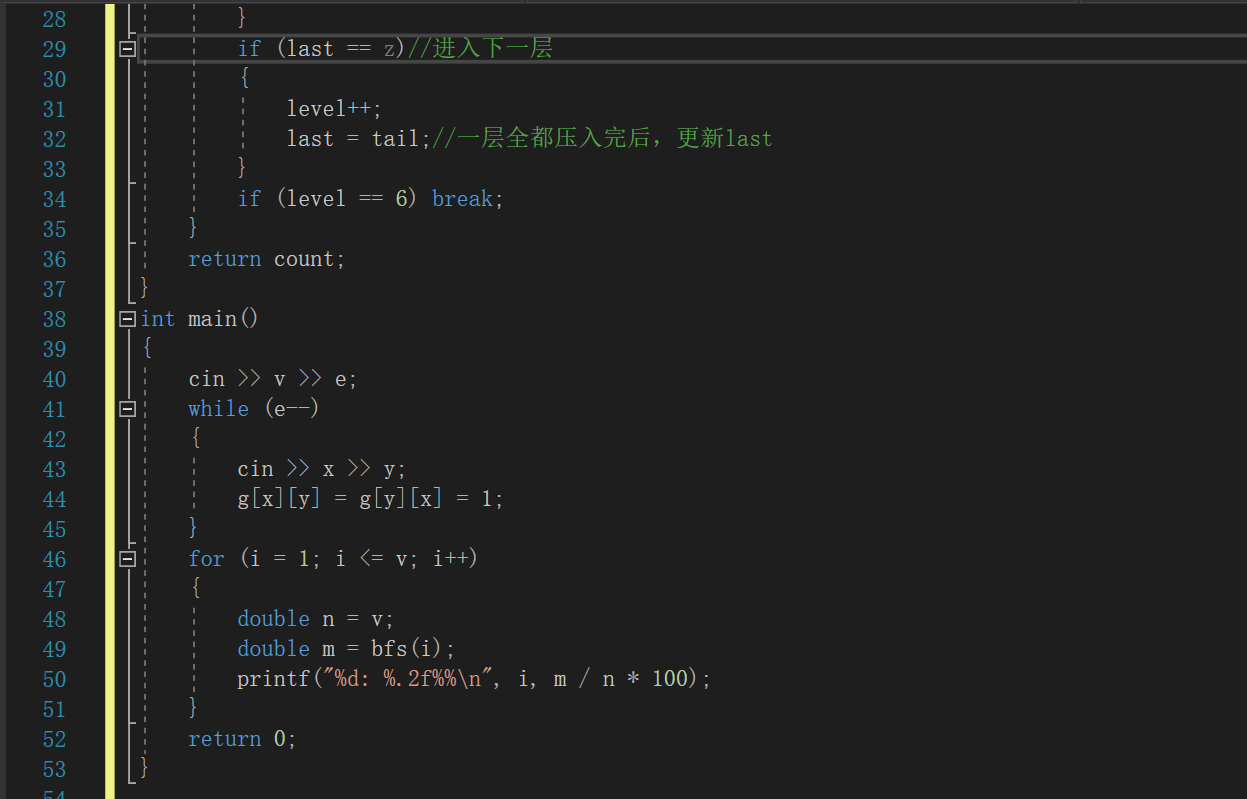
- bfs函数:
初始化各点为未访问状态
将第一个节点z入队同时标记他为已访问状态
当队不空的时候
z记录队首元素后即可将队首出队
遍历其他节点
if(和该点为相邻接点且未被访问过)
能通过六度空间认识的陌生人加一
将该节点入队并标记为已访问
tail记住最后一个入队节点的位置
if(队首元素和存放的一层最后一个元素相等)
层数加一
last更新为tail的值
if(层数=6)不符合六度空间要求,此时跳出循环
return回count
- main函数
循环读入边之间关系
遍历节点
m接收bfs返回的count
m/v*100即为输出的答案
2.2.2代码截图
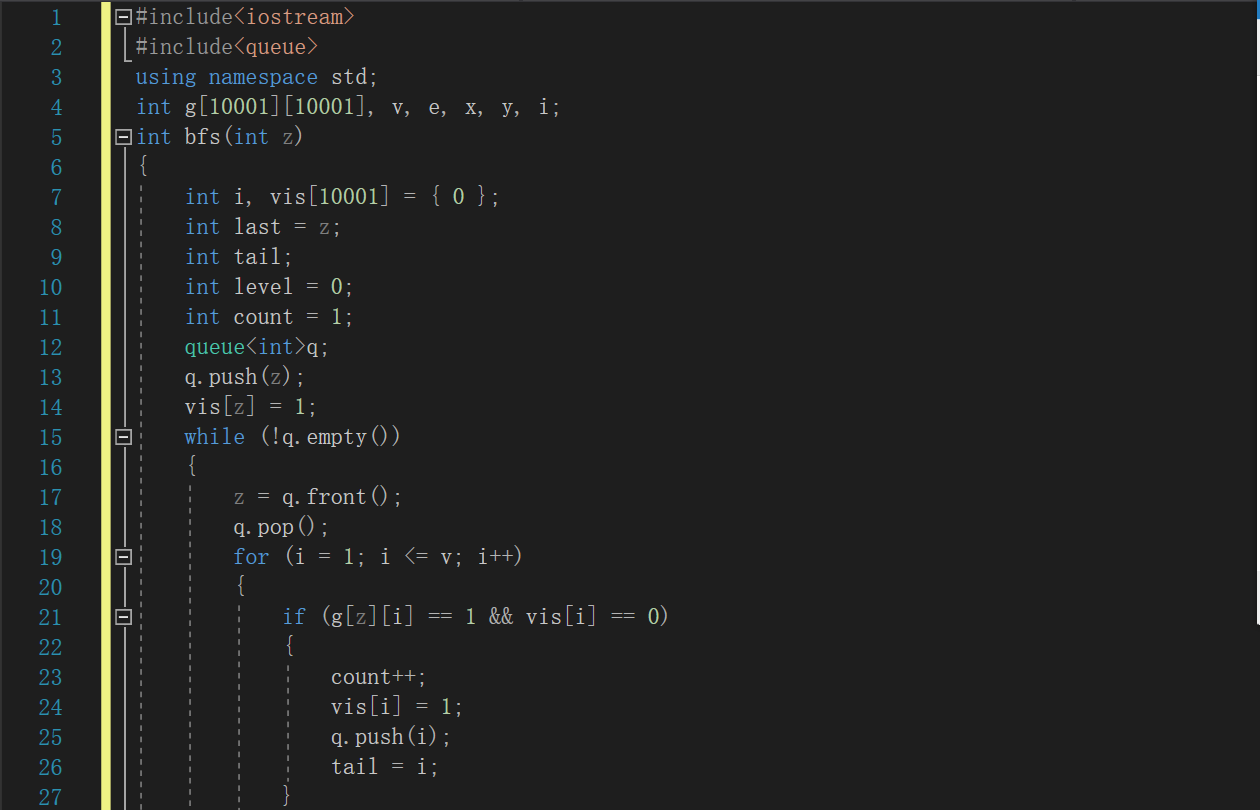
2.2.3PTA提交列表及说明

- A1:我发现好几题我用邻接表做都错误百出,用邻接矩阵一样的思路交上去反而对了,所以综上,还是能用邻接矩阵就不用邻接表
- A2:后面我去百度了一下,发现用邻接表那个运行时错误是因为自己直接把函数题代码复制过来,数组不够大导致越界
- A3:下面总结几种运行时错误的原因
- 数组越界访问(数组开大即可)
- 除数为零
- 堆栈溢出(大多是递归口出问题)
- 使用失效的迭代器
2.3 题目3:公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12
2.3.1设计思路
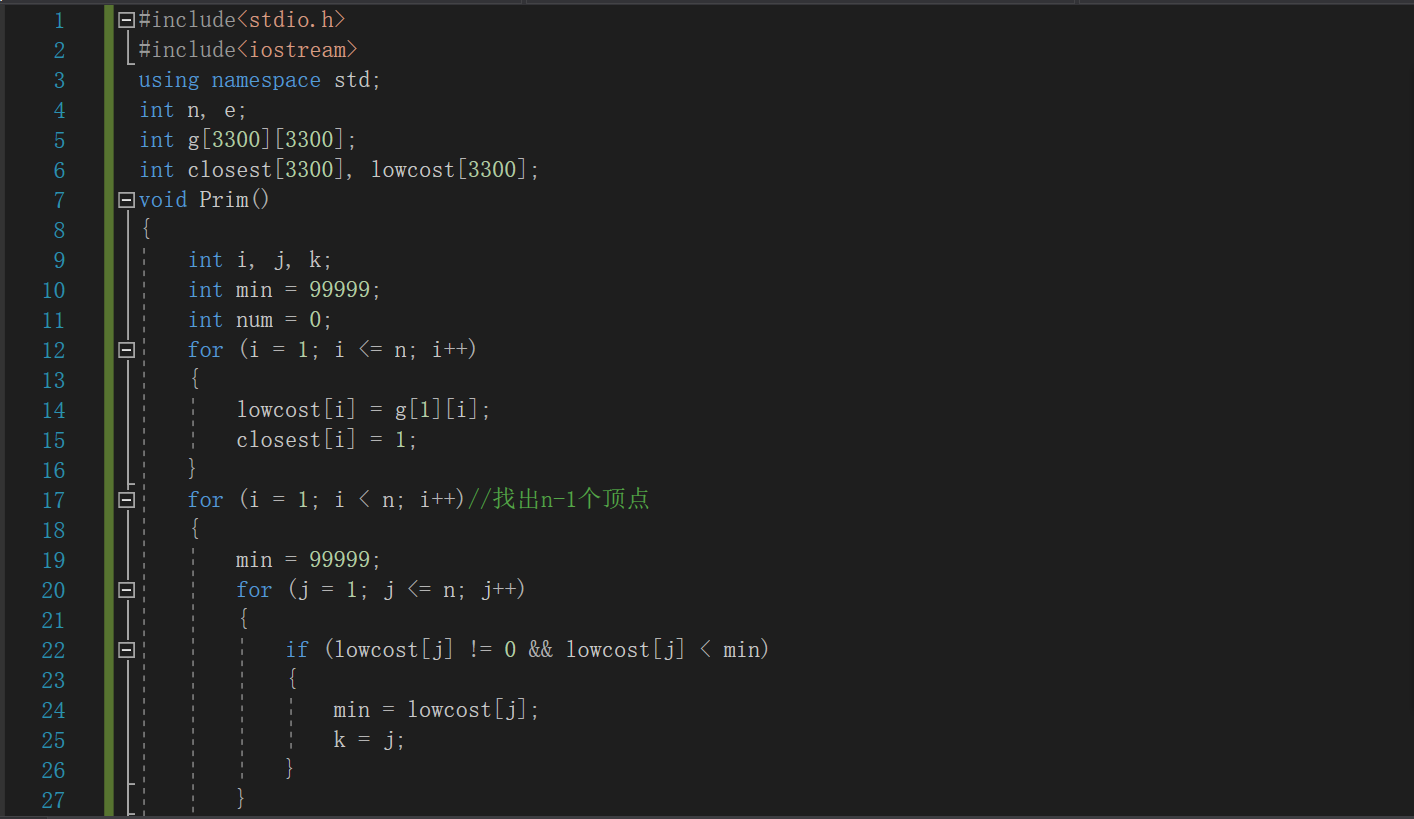
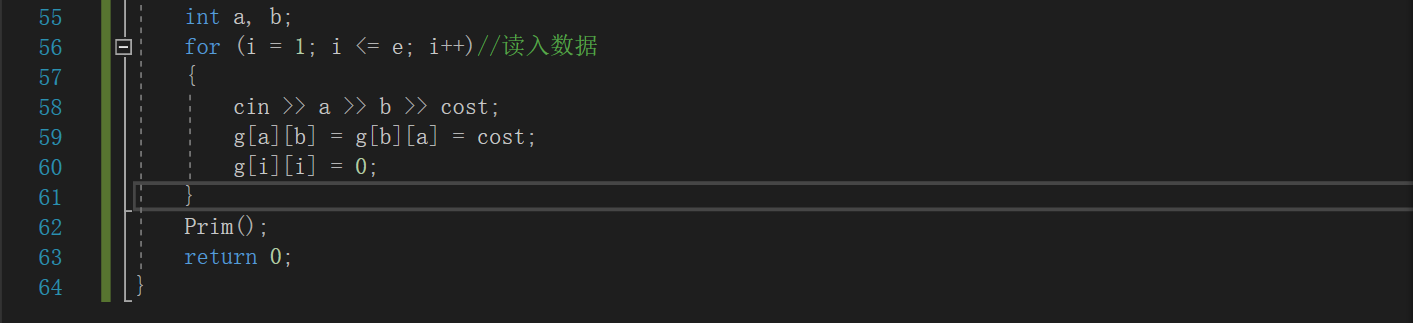
main函数
初始化权重为无穷
读入边之间的权重关系
Prim函数
循环将节点1的相邻边之间的权重存入数组lowcost,作为最小权重
for循环找出n-1个节点的最小权重
for循环遍历各个节点
if(权重不为0且不为无穷)
min记住此时权重,k记住该节点 j
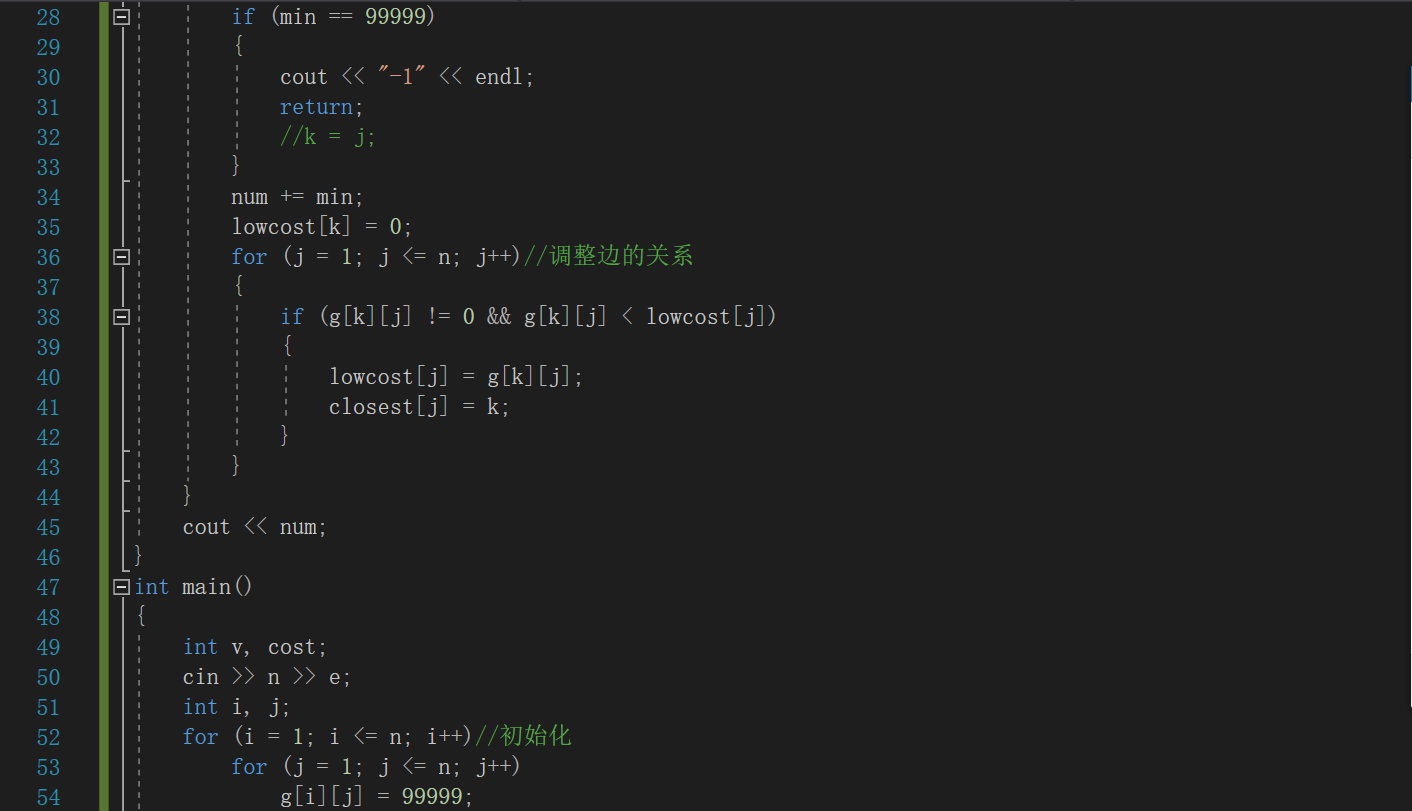
if(min为无穷)
非连通图,返回-1
num加上此时min,为修路最小花费
for(遍历节点调整边关系)
if(权重不为0且两点间权重小于lowcost存的)
调整lowcost为该权重,同时 j 的closest值改为k
end for
end for
输出最小花费num
2.3.2代码截图
2.3.3PTA提交列表及说明
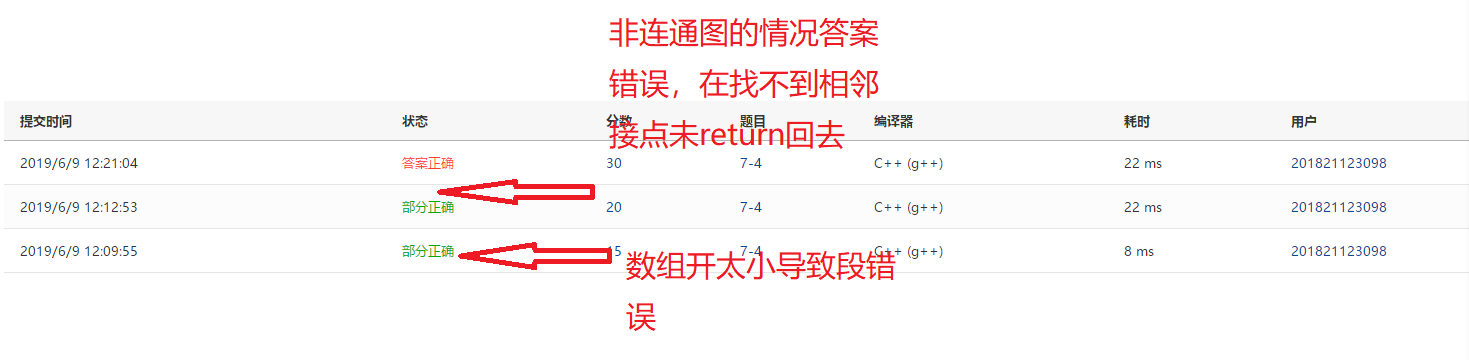

- 删除k=j该句即可
3、上机考试错题及处理办法
3.1.拓扑排序
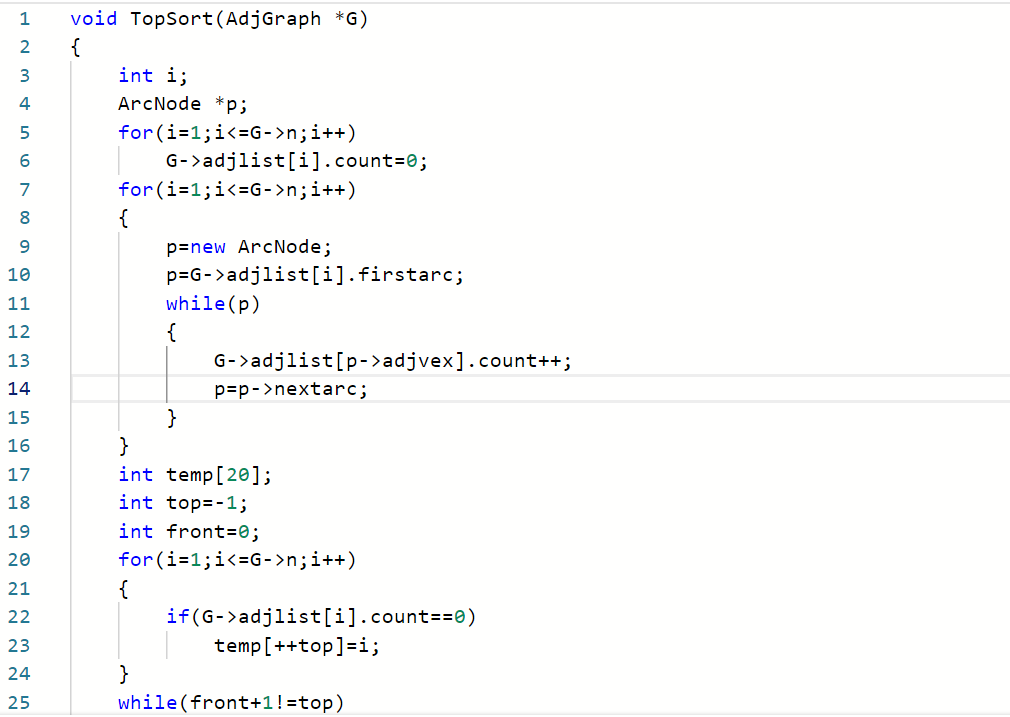
当时在深度广度函数题那里耗了好久,思路看着没错一直过不去,vs又不好用,拿到dev又不能给我指出明确的错误,真的是很急。后面一直通过目测,发现是多次new导致有问题,然后拓扑排序就只剩半个小时,只写了一半就交了,但源代码也有错误
- 源代码

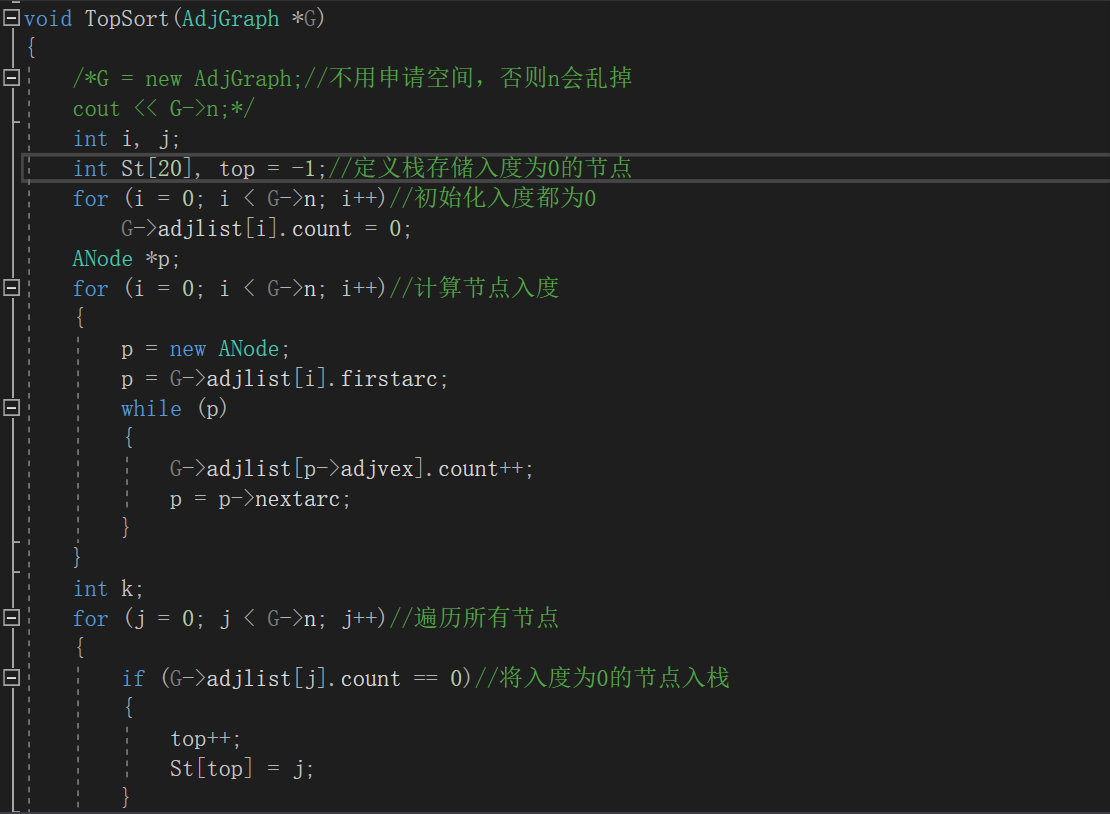
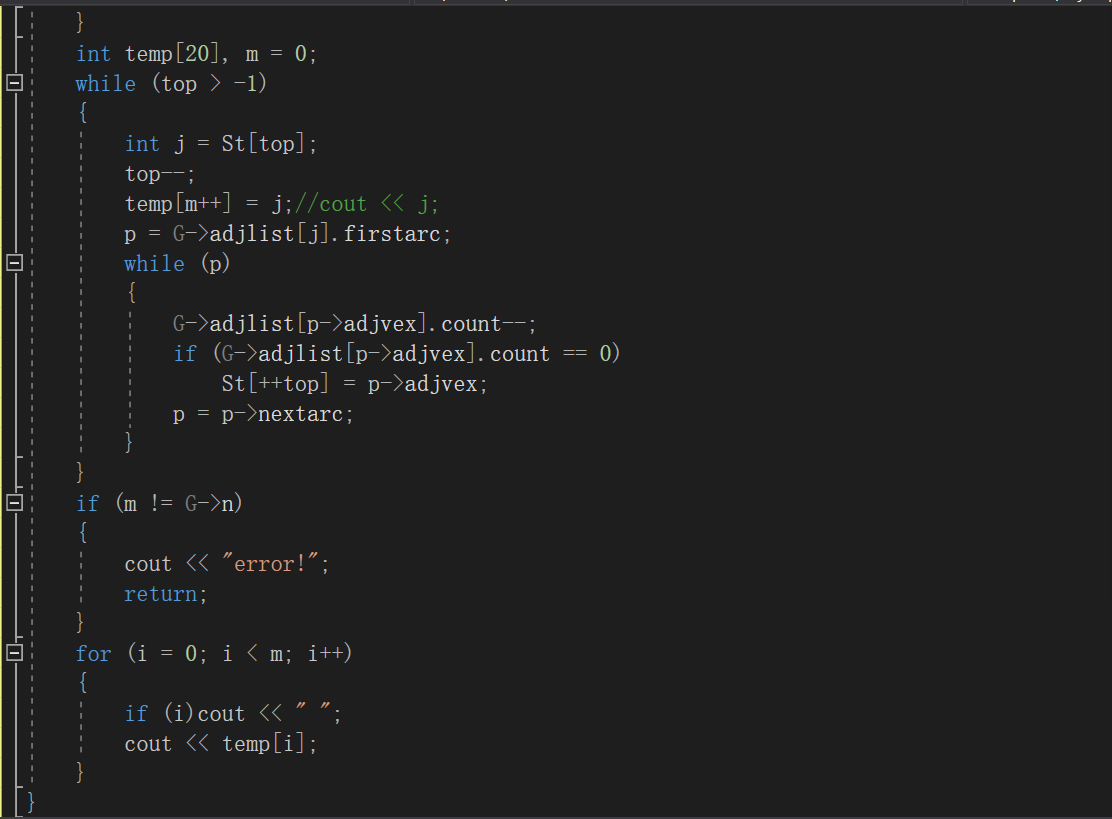
3.2 错的原因及处理方法

- 改正并且补齐后的代码如下
- 总结
图结构主要是自己练的不够多,他需要自己代码思路不是很多,直接套用模板就可以做出来,就深度广度遍历和那几种算法。在上机考时真没想到自己一题函数题都能改那么久才对。思路脑海里是有的,主要是一些细节问题,常不注意,而且自己阅读代码能力比较弱,无法马上知道错误,要经过好久的调试才会灵感一线,发现原来是这样。今后学习还得多学习他人优秀代码,哪怕是照着打一遍,都比看上个三四遍强。关于c++一些库函数的知识我正在积累并逐渐学者应用到实际中,积少成多,总会有收获的。



