15.函数式编程和偏函数

 

 

五、函数式编程

 

匿名函数与lambda

1、python允许用lambda关键字创造匿名函数

2、匿名是因为不需要以标准的def方式来声明

3、一个完整的lambda语句代表了一个表达式，这个表达式的定义体必须和声明放在同一行

lambda [arg1[, arg2, ... argN]]: expression

 

 例子1：

>>> a = lambda x, y: x + y
>>> print a(3, 4)
7

 

例子2：

>>> def add(x,y):           #定义一个加法函数
    return x+y              #返回两个参数的相加的值
 
>>> z=add(3,4)               
>>> print z 
7                                     #调用加法函数返回7
>>> lambda x,y:x+y
<function <lambda> at 0x0000020F385B86A8>   
#可以看到lambda是一个   function（函数）类对象
>>> f=lambda x,y:x+y          #功能实现的跟add(x,y)一样       
>>> f(1,2)
3
>>> f(3,4)
7
>>> def multiply(x,y):
    return x*y
 
>>> multiply(3,4)
12
>>> multiply=lambda x,y:x*y
>>> multiply(3,4)
12
>>> def subtract(x,y):
    return x-y
 
>>> subtract(3,4)
-1
>>> subtract=lambda x,y:x-y
>>> subtract(3,4)
-1
 
>>> def divide(x,y):
    return x/y
 
>>> divide(4,2)
2.0
>>> divide=lambda x,y:x/y
>>> divide(4,2)
2.0
 
#上面的乘法函数，减法函数，除法函数都可以用lambda表达式来代替，更方便

 

 

 

 

 

高阶函数

 

高阶函数

 

结论：

一个函数可以作为参数传给另外一个函数，或者一个函数为另外一个函数的返回值（若返回值为该函数本身，则为递归），满足其一则为高阶函数。

 

高阶函数英文叫Higher-order function。什么是高阶函数？我们以实际代码为例子，一步一步深入概念

 

变量可以指向函数

 

函数本身也可以赋值给变量，即：变量可以指向函数。如果一个变量指向了一个函数，那么，可以通过该变量来调用这个函数

以Python内置的求绝对值的函数abs()为例，调用该函数用以下代码：

>>> abs(-10)
10

 

但是，如果只写abs呢？

>>> abs
<built-in function abs>

 

可见，abs(-10)是函数调用，而abs是函数本身。

要获得函数调用结果，我们可以把结果赋值给变量：

>>> x = abs(-10)
>>> x
10

 

但是，如果把函数本身赋值给变量呢？

>>> f = abs
>>> f
<built-in function abs>

 

结论：函数本身也可以赋值给变量，即：变量可以指向函数。

如果一个变量指向了一个函数，那么，可否通过该变量来调用这个函数？用代码验证一下：

>>> f = abs
>>> f(-10)
10

 

成功！说明变量f现在已经指向了abs函数本身。直接调用abs()函数和调用变量f()完全相同。

 

 

函数名也是变量

那么函数名是什么呢？函数名其实就是指向函数的变量！对于abs()这个函数，完全可以把函数名abs看成变量，它指向一个可以计算绝对值的函数！

如果把abs指向其他对象，会有什么情况发生？

>>> abs = 10
>>> abs(-10)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: 'int' object is not callable

 

把abs指向10后，就无法通过abs(-10)调用该函数了！因为abs这个变量已经不指向求绝对值函数而是指向一个整数10！

当然实际代码绝对不能这么写，这里是为了说明函数名也是变量。要恢复abs函数，请重启Python交互环境。

注：由于abs函数实际上是定义在import builtins模块中的，所以要让修改abs变量的指向在其它模块也生效，要用import builtins; builtins.abs = 10。

 

传入函数

 

既然变量可以指向函数，函数的参数能接收变量，那么一个函数就可以接收另一个函数作为参数，这种函数就称之为高阶函数。

 

 一个最简单的高阶函数：

 

def add(x, y, f):
    return f(x) + f(y)

 

当我们调用add(-5, 6, abs)时，参数x，y和f分别接收-5，6和abs，根据函数定义，我们可以推导计算过程为：

 

x = -5
y = 6
f = abs
f(x) + f(y) ==> abs(-5) + abs(6) ==> 11
return 11

 

用代码验证一下

>>> add(-5, 6, abs)
11

 

编写高阶函数，就是让函数的参数能够接收别的函数。

小结

把函数作为参数传入，这样的函数称为高阶函数，函数式编程就是指这种高度抽象的编程范式。

 

函数作为返回值

高阶函数除了可以接受函数作为参数外，还可以把函数作为结果值返回。

我们来实现一个可变参数的求和。通常情况下，求和的函数是这样定义的：

def calc_sum(*args):
    ax = 0
    for n in args:
        ax = ax + n
    return ax

但是，如果不需要立刻求和，而是在后面的代码中，根据需要再计算怎么办？可以不返回求和的结果，而是返回求和的函数：

def lazy_sum(*args):
    def sum():
        ax = 0
        for n in args:
            ax = ax + n
        return ax
    return sum

 

当我们调用lazy_sum()时，返回的并不是求和结果，而是求和函数：

>>> f = lazy_sum(1, 3, 5, 7, 9)
>>> f
<function lazy_sum.<locals>.sum at 0x101c6ed90>

调用函数f时，才真正计算求和的结果：

>>> f()
25

 

在这个例子中，我们在函数lazy_sum中又定义了函数sum，并且，内部函数sum可以引用外部函数lazy_sum的参数和局部变量，当lazy_sum返回函数sum时，相关参数和变量都保存在返回的函数中，这种称为"闭包"的程序结构拥有极大的威力。

请再注意一点，当我们调用lazy_sum()时，每次调用都会返回一个新的函数，即使传入相同的参数：

>>> f1 = lazy_sum(1, 3, 5, 7, 9)
>>> f2 = lazy_sum(1, 3, 5, 7, 9)
>>> f1==f2
False

f1()和f2()的调用结果互不影响。

 

 内建高阶函数

 

map()函数

map()函数接收两个参数，一个是函数，一个是序列，map将传入的函数依次作用到序列的每个元素，并把结果作为新的list返回。

 

返回值
Python 2.x 返回列表。
Python 3.x 返回迭代器。

 

 举例说明，比如我们有一个函数f(x)=x²，要把这个函数作用在一个list [1, 2, 3, 4, 5, 6, 7, 8, 9] 上，就可以用 map() 实现如下：

 

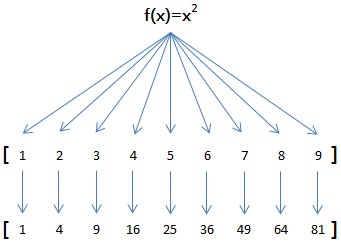
 现在，我们用Python代码实现：

>>> def f(x):
...     return x * x
...
>>> r = map(f, [1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> list(r)
[1, 4, 9, 16, 25, 36, 49, 64, 81]

 

如果不是交互式的话，可以这样做：

def f(x):
    return x * x

print map(f,[1, 2, 3, 4, 5, 6, 7, 8, 9])

或者

def f(x):
    return x * x

print map(f,[i for i in range(1,10)])

 

执行结果：

[1, 4, 9, 16, 25, 36, 49, 64, 81]

 map()传入的第一个参数是f，即函数对象本身。由于结果r是一个Iterator，Iterator是惰性序列，因此通过list()函数让它把整个序列都计算出来并返回一个list。
你可能会想，不需要 map() 函数，写一个循环，也可以计算出结果：

def f(x):
    return x * x

L = []
for n in [1, 2, 3, 4, 5, 6, 7, 8, 9]:
    L.append(f(n))
print L

执行结果：

[1, 4, 9, 16, 25, 36, 49, 64, 81]

 

 

的确可以，但是，从上面的循环代码，能一眼看明白"把f(x)作用在list的每一个元素并把结果生成一个新的list"吗？
所以， map() 作为高阶函数，事实上它把运算规则抽象了，因此，我们不但可以计算简单的f(x)=x ，还可以计算任意复杂的函数，比如，把这个list所有数字转为字符串：

def f(x):
    return x * x

print map(str, [1, 2, 3, 4, 5, 6, 7, 8, 9])

执行结果：

['1', '2', '3', '4', '5', '6', '7', '8', '9']

 只需要一行代码。

 

filter()函数

和 map() 类似， filter() 也接收一个函数和一个序列。和 map() 不同的时， filter() 把传入的函数依次作用于每个元素，然后根据返回值是 True 还是 False 决定保留还是丢弃该元素。

例如，在一个list中，删掉偶数，只保留奇数，可以这么写：

 

def is_odd(n):
    return n % 2 == 1
print filter(is_odd, [1, 2, 4, 5, 6, 9, 10, 15])

 

或者使用filter+lambda结合：

print filter(lambda n:n %2, [1, 2, 4, 5, 6, 9, 10, 15])

 

执行结果：

[1, 5, 9, 15]

 

 

reduce()函数

 

同样的接收两个参数，一个是函数，一个是可迭代对象 Iterable Object（eg: list列表）。reduce中的函数必须也要接收2个参数，执行时把前一个结果继续和序列的下一个元素做累积计算，其效果就是：

reduce(f, [x1, x2, x3, x4]) = f(f(f(x1, x2), x3), x4)

python2中，为内置函数

python3中，导入reduce, from functools import reduce

 

 

比方说对一个序列求和，就可以用reduce实现：

 

def add(x,y):
    return x + y

print reduce(add,[1,3,5,7,9])

执行结果：

25

 

阶乘

 

#!/usr/bin/env python
#coding:utf8

def mulit(x,y):
    return x * y

print reduce(mulit,[1,3,5,7,9])

 

执行结果：

945

 

 

 

sorted函数

 

 

列表里面提供了sort方法，其它数据结构没有.sorted方法可以对任何可迭代对象排序
sort方法支持原地排序(变量排序后，变量本身改变),sorted排序后返回一个新的列表，并不改变原有变量
默认sort和sorted方法由小到大进行排序排序，reverse=True时，由小到大进行排序

 

排序是在程序中经常用到的算法。无论使用冒泡排序还是快速排序，排序的核心是比较两个元素的大小。如果是数字，我们可以直接比较，但如果是字符串或者两个dict呢？直接比较数学上的大小是没有意义的，因此，比较的过程必须通过函数抽象出来。

 

1.sorted() 函数就可以对list进行排序

>> sorted([36, 5, 12, 9, 21])
[5, 9, 12, 21, 36]

2、sorted() 函数也是一个高阶函数，它还可以接收一个比较函数来实现自定义的排序。比如，如果要倒序排序，我们就可以自定义一个 reversed_cmp 函数：

def reversed_cmp(x, y):
　　if x > y:
　　　　return -1
　　if x < y:
　　　　return 1
　　return 0

传入自定义的比较函数 reversed_cmp ，就可以实现倒序排序：

>>> sorted([36, 5, 12, 9, 21], reversed_cmp)
[36, 21, 12, 9, 5]

 

我们再看一个字符串排序的例子：

>>> sorted(['bob', 'about', 'Zoo', 'Credit'])
['Credit', 'Zoo', 'about', 'bob']

默认情况下，对字符串排序，是按照ASCII的大小比较的，由于 'Z' < 'a' ，结果，大写字母 Z 会排在小写字母 a的前面。
现在，我们提出排序应该忽略大小写，按照字母序排序。要实现这个算法，不必对现有代码大加改动，只要我们能定义出忽略大小写的比较算法就可以：

def cmp_ignore_case(s1, s2):
　　u1 = s1.upper()
　　u2 = s2.upper()
　　if u1 < u2:
　　　　return -1
　　if u1 > u2:
　　　　return 1
　　return 0

忽略大小写来比较两个字符串，实际上就是先把字符串都变成大写（或者都变成小写），再比较。
这样，我们给 sorted 传入上述比较函数，即可实现忽略大小写的排序：

>>> sorted(['bob', 'about', 'Zoo', 'Credit'], cmp_ignore_case)
['about', 'bob', 'Credit', 'Zoo']

 

 

 

偏函数

 

 

偏函数（Partial function）是通过将一个函数的部分参数预先绑定为某些值，从而得到一个新的具有较少可变参数的函数。

在Python中，可以通过functools中的partial高阶函数来实现偏函数功能。

首先介绍下偏函数partial。首先借助help来看下partial的定义

 

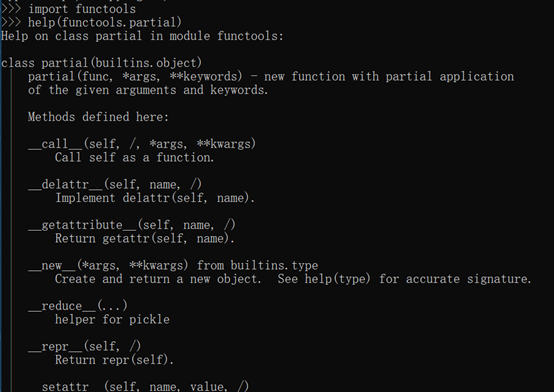
首先来说下第一行解释的意思：

partial 一共有三个部分：

（1）第一部分也就是第一个参数，是一个函数，这个函数可以是你定义的，也可以是Python内置函数

（2）第二部分是一个可变参数，*args，比如内置函数max的参数就是一个可变参数，max（1,2,3,4,5）=5

（3）第三部分是一个关键字参数，比如内置函数int的第二个参数就是命名关键字参数，默认base=10，表示int转换时默认是10进制的：

partial函数的作用就是：将所作用的函数作为partial（）函数的第一个参数，原函数的各个参数依次作为partial（）函数的后续参数，原函数有关键字参数的一定要带上关键字，没有的话，按原有参数顺序进行补充。

 

>>> from operator import add
>>> from functools import partial
>>> add10 = partial(add, 10)
>>> print add10(25)
35

 

 

 

myadd.py内容：

#!/usr/bin/env python
#coding:utf8

from functools import partial

def add(x,y):
    return x + y 

if __name__ == "__main__":
    print add(10, 8)
    print add(10,30)
    print add(10,5)
    add10 = partial(add,10)
    print add10(50) 

 

执行结果

18
40
15
60

 

编写一个窗口程序，要求如下
1. 窗口程序提供三个按钮

#!/usr/bin/env python
#coding:utf8

import Tkinter
from functools import partial

root = Tkinter.Tk()
MyButton = partial(Tkinter.Button,root,fg='white',bg='blue')
b1 = MyButton(text="Button1")
b2 = MyButton(text="Button")
qb = MyButton(text='quit',command=root.quit)
b1.pack()
b2.pack()
qb.pack()
Tkinter.mainloop()

 编写一个窗口程序，要求如下
1. 窗口程序提供三个按钮
2. 其中两个按钮的前景色均为白色，背景色为蓝色
3. 第三个按钮前景色为红色，背景色为红色
4. 按下第三个按钮后，程序退出

 方案

python 可以使用 tkinter 模块实现 GUI 编程，系统默认没有安装相关模块，需要将对
应的 RPM 安装好。
由于创建按钮的实例需要很多参数，同时这些参数使用相同的值，那么可以使用偏函数
的方式将这些值固定下来以简化程序的编写。

实现此案例需要按照如下步骤进行。
步骤一：安装相关的程序包
[root@py01 bin]# yum install -y tkinter

 

步骤二：编写脚本

 

#!/usr/bin/env python
#coding:utf-8
import Tkinter #导入模块，用于编写 GUI 界面
from functools import partial #仅导入偏函数相关的功能函数

root = Tkinter.Tk() #创建背景窗口

#使用偏函数定义按钮的默认参数
MyButton = partial(Tkinter.Button, root, fg = 'white', bg = 'blue')
b1 = MyButton(text = 'Button 1') #创建按钮，指定按钮上的文字
b2 = MyButton(text = 'Button 2')
qb = MyButton(text = 'QUIT', bg = 'red', command = root.quit)

b1.pack() #将安装到背景窗口上
b2.pack()
qb.pack(fill = Tkinter.X, expand = True)
root.title('PFAs!') #设置背景窗口标题
root.mainloop() #启动窗口程序

执行结果：

 

二、偏函数的使用

A、偏函数的第二个部分(可变参数)，按原有函数的参数顺序进行补充，参数将作用在原函数上，最后偏函数返回一个新函数（类似于，装饰器decorator，对于函数进行二次包装，产生特殊效果；但又不同于装饰器，偏函数产生了一个新函数，而装饰器，可改变被装饰函数的函数入口地址也可以不影响原函数）

 

注意：如果不理解装饰器，可以先去看一下装饰器的内容

案例：我们定义一个sum函数，参数为*args可变，计算这些可变参数的和。

扩展：我们想要对sum函数求和后的结果，再加上10加上20甚至加更多，得到一个新的结果

实现：我们分别用decorator和partial来实现，对比一下二者的区别

 

（一）装饰器 decorator 实现

 

test.py

# /usr/bin/env Python3
# -*- encoding:UTF-8 -*-

from functools import wraps

def sum_add(*args1): #我们要给我们的装饰器decorator，带上参数
    def decorator(func):
        @wraps(func) #加上这句，原函数func被decorator作用后，函数性质不变
        def my_sum(*args2): #注意，参数要和原函数保持一致，真正实行扩展功能的是外层的装饰器
            my_s = 0
            for n in args1:
                my_s = my_s +n #这个是我们新加的求和结果
            return func(*args2) + my_s #这个，我们在原求和函数的结果上再加上s，并返回这个值
        return my_sum #返回my_sum函数，该函数扩展原函数的功能
    return decorator  #返回我们的装饰器

@sum_add(10,20) #启用装饰器 对sum函数进行功能扩展 
def sum(*args):
    s = 0
    for n in args:
        s = s+n
    return s
print(sum(1,2,3,4,5))
print(sum.__name__)

 

sum(1,2,3,4,5)返回的结果绝不是15，这样就失去了装饰器存在的意义，当然，这里，我们知道，sum最后返回的值应该是10+20+15 = 45，这样一来，我们的decorator就实现了我们想要的扩展功能，最后，发现，原函数sum的name属性，仍然是sum，说明，这种装饰扩展功能，不影响我们的原函数：

 

（二）偏函数 partial function 实现

这才是我们本篇的重点，准备好了，我们就开始：

我们先来看下普通函数，我们是怎么来实现

A：普通函数可变参数顺序执行

 

#!/usr/bin/env python
#coding:utf8


def sum(*args):
    s = 0
    for n in args:
        s = s + n
    return s


print(sum(10, 20) + sum(1, 2, 3, 4, 5))

 

 

 

我们如果想实现+10+20的效果，必须写两遍sum，这样写，显然是最易懂的，但是，却显得很邋遢

 

 

B：普通函数可变参数加关键字参数组合

针对上面的A过程，我们改下代码，使我们的代码看起来稍显复杂，但是略显专业：

 

 

#!/usr/bin/env python
#coding:utf8




def sum(*args, **others):
    s = 0
    for n in args:
        s = s + n
    s1 = 0
    for k in others:
        s1 = s1 + others[k]  # 我们还要算一下，关键字参数里蕴藏的求和结果，k是dict中的关键字key
    return s + s1  # 最终，我们实现扩展功能，顺序参数和关键字参数结果相加


D = {'value1': 10, 'value2': 20}
print(sum(1, 2, 3, 4, 5, **D))

 

 

 

 

代码看起来，是显得专业了，但是感觉冗余，没必要

 

C：偏函数可变参数顺序填充一步到位

 

 

上面A和B我们都说过了，这两种方式都不好，显然，这么简单的事情，我们不必麻烦decorator了，那我们还有办法没？有，Python，给我们提供了偏函数，来吧，主角登场：

提示：两种使用partial功能方式

 

（1）import functools                        -->functools.partial(func,*args)
（2）from   functools import partial -->partial(func,*args)

 

 

我们这里选第二种,我们看下demo：

 

 

#!/usr/bin/env python
#coding:utf8


from functools import partial


def sum(*args):
    s = 0
    for n in args:
        s = s + n
    return s


sum_add_10 = partial(sum, 10)  # 10 作用在sum第一个参数的位置
sum_add_10_20 = partial(sum, 10, 20)  # 10 20 分别作用在sum第一个和第二个参数的位置
print('A____________我们看下原函数sum的函数地址入口：')
print(sum)
print('B______我们看下partial函数返回函数的地址入口：')
print(partial(sum, 10))
print(sum_add_10(1, 2, 3, 4, 5))  # --> 10 + 1 + 2 + 3 + 4 + 5 = 25
print(sum_add_10_20(1, 2, 3, 4, 5))  # --> 10 + 20 + 1 + 2 + 3 + 4 + 5 = 45

 

 

 

可以看出，我们针对sum函数的求和结果，再加上10，或者加10加20，甚至加更多，都是可以通过偏函数来实现的，注意偏函数的第二部分，参数是可变的，是按顺序走的，因此，偏函数产生的新函数，sum_add_10 实际上等同于sum(10,*args)：

通过几个例子，我们最终发现，还是偏函数比较方便，一行代码就搞定了，而且新定义的函数，可以根据函数名很容易知道，这个函数扩展的原函数是哪个，实现的效果是什么：

 

 

B、偏函数的第三个部分(关键字参数)，按原有函数的关键字参数进行填补，参数将作用在原函数上，最后偏函数返回一个新函数

 

 

 

案例：我们定义一个mod求余函数，两个参数，一个是被除数，一个是除数，除数我们这里用命名关键字参数表示，默认值2

 

扩展：我们的除数不固定，可以是对2就行求余，也可以对3，对4，总之我们需要指定除数的值

 

返回结果： True 或 False

 

实现：原函数实现和partial函数实现

 

demo如下：

 

 

 

#!/usr/bin/env python
#coding:utf8


import  functools
def mod(m,key=2):
    return m % key == 0
mod_to_2 = functools.partial(mod,key=2)
print('A__3___使用原函数的默认关键字参数对2进行求余：')
print(mod(3))                           #对2进行求余-- 原函数 使用默认参数
print('B__3___使用偏函数对2进行求余：')
print(mod_to_2(3))                      #对2进行求余-- 新函数 --偏函数产生
mod_to_5 = functools.partial(mod,key=5)
print('C__25___使用原函数的关键字参数对5进行求余：')
print(mod(25,key=5))                    #对5进行求余 -- 原函数
print('D__25___使用偏函数对5进行求余：')
print(mod_to_5(25))                     #对5进行求余 -- 新函数--偏函数产生  + 3 + 4 + 5 = 45

 

 

我们发现，实际上，偏函数的作用，其实和原函数差不多，只不过，我们要多次调用原函数的时候，有些参数，我们需要多次手动的去提供值，比如上述的对5进行求余，如果我们想知道，15,45,30这些数是否能够被5整除，那么，我们用原函数的话，就需要写三次，key=5，然而，我们用偏函数的话，只需要重复调用新产生的函数mod_to_5（15 or 45 or 30）即可，至于除数5，偏函数已经为我们设定了，因此：

当函数的参数个数太多，需要简化时，使用 functools.partial 可以创建一个新的函数，这个新函数可以固定住原函数的部分参数，从而在调用时更简单。当然，decorator也可以实现，如果，我们不嫌麻烦的话。

 

偏函数参考：https://www.cnblogs.com/huyangblog/p/8999866.html