GIS算法基础(四)平面坐标变换(变换矩阵算法实现)
目录
po一个B站线性代数学习资料,这个作者很好地解释线性代数操作空间的本质。
一、平面直角坐标系的建立
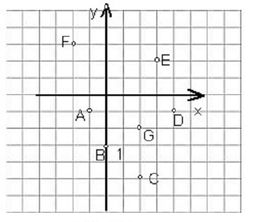
在平面上选一点作为直角坐标的原点,过该原点作相互垂直的两轴,就建立起了平面直角坐标系,如上图所示。
在代码中,我们可以用一个类表示一个点实体,他由一串坐标组成,但是,如果这些点如果位于不同的坐标系中,该怎么转换呢?通过对X,Y的操作,比如平移就在相应的X,Y分量上加偏移量,我们就可以实现。那如果,我们既要平移,又要旋转,或者一系列的对点实体的操作,该怎么实现?这个时候就可以用到平面坐标变换矩阵。
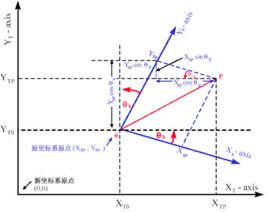
二、平面坐标变换矩阵
“变换矩阵是数学线性代数中的一个概念。在线性代数中,线性变换能够用矩阵表示。如果T是一个把Rn映射到Rm的线性变换,且x是一个具有n个元素的列向量 ,那么我们把m×n的矩阵A,称为T的变换矩阵。”
-------百度百科-变换矩阵
其实没有这么复杂,就是我们通过对一个坐标串构成的矩阵与某个矩阵相乘,得到的新矩阵包含了我们所要的坐标的信息。这个"某个矩阵"在这里就是屏幕坐标变换矩阵。
怎么构建 矩阵吧,矩阵的构建可以用二维数组实现。这个不是算法的重点,所以我就不po代码了,想看代码可以到我的github上看
https://github.com/XiaoZhong233/GIS_ALG/blob/master/src/scau/gz/zhw/BasicTransform.java
平面坐标变换矩阵可由下式表示:
/**
* |a d g|
* T= |b e h| |a d| |g|
* |c f i| |b e| 负责对图形的缩放,旋转,对称,错切 。[c f] 负责对图形进行平移变换 |h| 负责投影变换
*/
构建代码:
public class SurfaceTransformationMatrix {
private double a,b,c,d,e,f,g,h,i;
private double[][] data= {{a,d,g},{b,e,h},{c,f,i}};
private Matrix matrix;
public SurfaceTransformationMatrix() {
this.matrix = new Matrix(data);
}
public SurfaceTransformationMatrix(double[][] data) {
this.matrix = new Matrix(data);
}
public Matrix getMatrix() {
return matrix;
}
}
三、平移变换
公式如下:
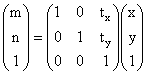
(m,n)是变换后的坐标,(x,y)是变换前的坐标,tx,ty分别对应x轴,y轴的偏移量
构建代码:
public class TransformMatrix extends SurfaceTransformationMatrix{
private Matrix matrix;
public TransformMatrix(double Tx,double Ty) {
super(new double[][]{{1,0,0},{0,1,0},{Tx,Ty,1}});
this.matrix = super.getMatrix();
}
public Matrix getTransformMatrix() {
return matrix;
}
}
平移算法:
/**
* 平移算法
* @param point
* @param x x正方向偏移量
* @param y y正方向偏移量
* @return
*/
public static Point transform(Point point,double x,double y) {
Matrix matrix = new TransformMatrix(x, y).getTransformMatrix();
double [][] data= {{point.getX(),point.getY(),1}};
Matrix pointMatrix = new Matrix(data);
Matrix result = pointMatrix.RightMultiMatrix(matrix);
//System.out.println("平移后的点 :"+new Point(result.getMatrix()[0][0], result.getMatrix()[0][1]).toString());
return new Point(result.getMatrix()[0][0], result.getMatrix()[0][1]);
}
public static Line transform(Line line,double x,double y) {
Point start = line.getStart();
Point end = line.getEnd();
Point newStart = transform(start, x, y);
Point newEnd = transform(end, x, y);
return new Line(newStart,newEnd);
}
public static Polygon transform(Polygon polygon,double x,double y) {
Point[] points = polygon.getPoints();
Point[] result = new Point[points.length];
for(int i=0;i<points.length;i++) {
result[i]=transform(points[i], x, y);
//System.out.println("result :"+result[i].toString());
}
return new Polygon(result, polygon.isClose());
}接下来的变换基本都和这个变换的例子差不多,无非是参数的变化
四、比例变换
变换公式:[x* y* 1] = [x y 1] x [{Sx,0,0},{0,Sy,0},{0,0,1}] = [Sx*x Sy*y 1]
因为公式没找到图,就用二维数组来表示
x*,y*是x,y变换后的坐标
变换关系如下
(1)当Sx = Sy = 1 时,为恒等比例变换,就是图形不变
(2)当Sx = Sy > 1 时,图形沿两个坐标轴方向等比例放大。
(3)当Sx = Sy < 1 时,图形沿两个坐标轴方向等比例缩小。
(4)当Sx != Sy 时,图形沿两个坐标轴方向做非均匀的比例变换。
构建代码:
public class ScaleMtrix extends SurfaceTransformationMatrix{
private Matrix matrix;
public ScaleMtrix(double Sx,double Sy) {
// TODO Auto-generated constructor stub
super(new double[][]{{Sx,0,0},{0,Sy,0},{0,0,1}});
this.matrix = super.getMatrix();
}
public Matrix getScaleMatrix() {
return matrix;
}
}
算法:
/**
* 比例变换算法
* x=y时,恒比例放大或缩小
* x!=y时,图形沿两个坐标轴方向做非均匀比例变换
* @param point
* @param x
* @param y
* @return
*/
public static Point scale(Point point,double x,double y) {
Matrix matrix = new ScaleMtrix(x, y).getScaleMatrix();
double [][] data= {{point.getX(),point.getY(),1}};
Matrix pointMatrix = new Matrix(data);
Matrix result = pointMatrix.RightMultiMatrix(matrix);
return new Point(result.getMatrix()[0][0], result.getMatrix()[0][1]);
}
public static Line scale(Line line,double x,double y) {
Point start = line.getStart();
Point end = line.getEnd();
Point newStart = scale(start, x, y);
Point newEnd = scale(end, x, y);
return new Line(newStart,newEnd);
}
public static Polygon scale(Polygon polygon,double x,double y) {
Point[] points = polygon.getPoints();
Point[] result = new Point[points.length];
for(int i=0;i<points.length;i++) {
result[i]=scale(points[i], x, y);
//System.out.println("result :"+result[i].toString());
}
return new Polygon(result, polygon.isClose());
}
五、对称变换
公式如下:
[x*,y*,1] = [x,y,1] x [{a,d,0},{b,e,0},{0,0,1}] = [ax+by dx+ey 1]
变换关系:
(1)当b=d=0,a=-1,e=1时,产生与y轴对称的反射图形
(2)当b=d=0,a=1,e=-1时,产生与x轴对称的反射图形
(3)当b=d=0,a=e=-1时,产生与原点对称的反射图形
(4)当b=d=1,a=e=0时,产生与直线y=x对称的反射图形
(5)当b=d=-1,a=e=0时,产生与直线y=-x对称的反射图形
构建代码:
/**
* 对称变换矩阵
* @author Administrator
*
*/
public class SymmetryMatrix extends SurfaceTransformationMatrix{
private Matrix matrix;
public SymmetryMatrix(double a,double b,double d,double e) {
// TODO Auto-generated constructor stub
super(new double[][] {{a,d,0},{b,e,0},{0,0,1}});
this.matrix = super.getMatrix();
}
public Matrix getSymmetryMatrix() {
return matrix;
}
}算法:
/**
* 对称变换
* @param point
* @param symmetryType 枚举类型
* @return
*/
public static Point symmetry(Point point,SymmetryType symmetryType) {
Matrix matrix;
switch (symmetryType) {
case xAxis:
matrix = new SymmetryMatrix(1, 0, 0, -1).getSymmetryMatrix();
break;
case yAxis:
matrix = new SymmetryMatrix(-1, 0, 0, 1).getSymmetryMatrix();
break;
case yx:
matrix = new SymmetryMatrix(0, 1, 1, 0).getSymmetryMatrix();
break;
case anti_yx:
matrix = new SymmetryMatrix(0, -1, -1, 0).getSymmetryMatrix();
break;
case origin:
matrix = new SymmetryMatrix(-1, 0, 0, -1).getSymmetryMatrix();
default:
matrix = new SymmetryMatrix(-1, 0, 0, -1).getSymmetryMatrix();
break;
}
double [][] data= {{point.getX(),point.getY(),1}};
Matrix pointMatrix = new Matrix(data);
Matrix result = pointMatrix.RightMultiMatrix(matrix);
return new Point(result.getMatrix()[0][0], result.getMatrix()[0][1]);
}
六、旋转变换
公式如下:
[x*,y*,1] =
[x,y,1] x [{cosa,sina,0},{-sina,cosa,0},{0,0,1}] = [xcosa-ysina xsina+ycosa 1]
a是二维图形绕原点顺时针旋转a角。
构建代码:
public class RotateMatrix extends SurfaceTransformationMatrix{
private Matrix matrix;
public RotateMatrix(double angle) {
// TODO Auto-generated constructor stub
super(new double[][] {{Math.cos(Math.toRadians(angle)),Math.sin(Math.toRadians(angle)),0},
{-Math.sin(Math.toRadians(angle)),Math.cos(Math.toRadians(angle)),0},
{0,0,1}});
this.matrix = super.getMatrix();
}
public Matrix getRotateMatrix() {
return matrix;
}
}算法:
/**
* 旋转变换
* @param point
* @param angle 角度制单位
* @return
*/
public static Point rotate(Point point,double angle) {
Matrix matrix = new RotateMatrix(angle).getRotateMatrix();
double [][] data= {{point.getX(),point.getY(),1}};
Matrix pointMatrix = new Matrix(data);
Matrix result = pointMatrix.RightMultiMatrix(matrix);
return new Point(result.getMatrix()[0][0], result.getMatrix()[0][1]);
}
七、错切变换
公式如下:
[x*,y*,1] = [x,y,1] * [{1,d,0},{b,1,0},{0,0,1}] = [x+by,dx+y,1]
x*,y*为变换后的坐标。
变换关系如下:
(1)当d=0时,x*=x+by,y*=y,此时图形的y坐标不变,x坐标随初值(x,y)及变换系数b而作线性变换;若b>0,则图形沿+x方向做错切位移;b<0图形沿-x方向做错切位移。
(2)当b=0时,x*=x,y*=dx+y,此时图形的x坐标不变,y坐标随初值(x,y)及变换系数d做线性变换;如d>0,则图形沿+y方向作错切变换;d<0时,图形沿-y方向做错切位移。
(3)当b!=0时,且d!=0时,x*=x+by,y*=dx+y,图形沿x,y两个方向错切位移。

构建代码:
public class MiscutMatrix extends SurfaceTransformationMatrix{
private Matrix matrix;
public MiscutMatrix(double d,double b) {
// TODO Auto-generated constructor stub
super(new double[][] {{1,d,0},{b,1,0},{0,0,1}});
this.matrix = super.getMatrix();
}
public Matrix getMiscutMatrix(){
return matrix;
}
}算法如下:
/**
* 错切变换
* @param point
* @param b=0,y轴随变换系数d变换 b>0,图形沿+y方向做错切变换,b<0,图形沿-y方向做错切变换
* @param d=0,y轴随变换系数b变换 b>0,图形沿+x方向做错切变换,b<0,图形沿-x方向做错切变换
* b!=0 && d!=0时,x*=x+by y*=dx+y 图形沿x,y两个方向做错切变换
* @return
*/
public static Point miscut(Point point,double b,double d) {
Matrix matrix = new MiscutMatrix(b,d).getMiscutMatrix();
double [][] data= {{point.getX(),point.getY(),1}};
Matrix pointMatrix = new Matrix(data);
Matrix result = pointMatrix.RightMultiMatrix(matrix);
return new Point(result.getMatrix()[0][0], result.getMatrix()[0][1]);
}
八、复合变换
复合变换是指图形做一次以上的几何变换,变换结果是每次变换矩阵相乘。
(1)、复合平移
直接上代码吧,就直接几个平移矩阵相乘
/**
* 复合平移
* @param point
* @param matrixs
* @return
*/
public static Point complexTransform(Point point,TransformMatrix...matrixs) {
int len = matrixs.length;
Matrix matrix = matrixs[0].getTransformMatrix();
for(int i=1;i<len;i++) {
matrix = matrix.RightMultiMatrix(matrixs[i].getTransformMatrix());
}
double [][] data= {{point.getX(),point.getY(),1}};
Matrix pointMatrix = new Matrix(data);
Matrix result = pointMatrix.RightMultiMatrix(matrix);
return new Point(result.getMatrix()[0][0], result.getMatrix()[0][1]);
}
(2)复合比例变换
/**
* 复合比例变换
* @param point
* @param matrixs
* @return
*/
public static Point complexScale(Point point,ScaleMtrix...matrixs) {
int len = matrixs.length;
Matrix matrix = matrixs[0].getScaleMatrix();
for(int i=1;i<len;i++) {
matrix = matrix.RightMultiMatrix(matrixs[i].getScaleMatrix());
}
double [][] data= {{point.getX(),point.getY(),1}};
Matrix pointMatrix = new Matrix(data);
Matrix result = pointMatrix.RightMultiMatrix(matrix);
return new Point(result.getMatrix()[0][0], result.getMatrix()[0][1]);
}
(3)复合旋转
/**
* 复合旋转变换
* @param point
* @param matrixs
* @return
*/
public static Point complexRotate(Point point,RotateMatrix ...matrixs) {
int len = matrixs.length;
Matrix matrix = matrixs[0].getRotateMatrix();
for(int i=1;i<len;i++) {
matrix = matrix.RightMultiMatrix(matrixs[i].getRotateMatrix());
}
double [][] data= {{point.getX(),point.getY(),1}};
Matrix pointMatrix = new Matrix(data);
Matrix result = pointMatrix.RightMultiMatrix(matrix);
return new Point(result.getMatrix()[0][0], result.getMatrix()[0][1]);
}
比例,旋转变换是与参考的有关的,上面的都是相对于原点的比例变换,如果要参考某个(m,n)点做比例 ,旋转变换,其变换过程就是先把该坐标系的原点移到(m,n)上来,然后做了旋转或比例变换,然后再移回去。
(4)相对某点的比例变换
/**
* 相对于某点的比例变换
* @param point 待变换的点
* @param center 相对点
* @param x
* @param y
* @return
*/
public static Point scaleAround(Point point,Point center,double x,double y) {
TransformMatrix t1 = new TransformMatrix(-center.getX(), -center.getY());
ScaleMtrix scaleMtrix = new ScaleMtrix(x, y);
TransformMatrix t2 = new TransformMatrix(center.getX(), center.getY());
return complexTransmit(point, t1,scaleMtrix,t2);
}(5)相对某点的选址变换
/**
* 围绕某点的旋转变换
* @param point 待变换的点
* @param center 相对点
* @param angle
* @return
*/
public static Point rotateAround(Point point,Point center,double angle) {
TransformMatrix t1 = new TransformMatrix(-center.getX(), -center.getY());
RotateMatrix rotateMatrix = new RotateMatrix(angle);
TransformMatrix t2 = new TransformMatrix(center.getX(), center.getY());
return complexTransmit(point, t1,rotateMatrix,t2);
}
最后 po上我github地址,有需要的同学可以看看
https://github.com/XiaoZhong233/GIS_ALG/blob/master/src/scau/gz/zhw/BasicTransform.java


