GIS算法基础(六)矢量数据向栅格数据的转换(面转换的射线算法实现)
面状换的射线算法已经放在github上:
https://github.com/XiaoZhong233/GIS_ALG/blob/master/src/scau/gz/zhw/Raster.java
目录
一、常见的面转换算法
面状矢量数据是由闭合的线段组成的,在向栅格数据转换的过程中,可以先把边界做线状栅格化(线状栅格化的方法在算法基础)(五)中已经实现),剩下的工作其实就是填充面状要素。所以面状要素的栅格化又称为多边形填充,即在矢量表达的多边形边界内部的所有栅格点上赋以相应的多边形编码。
1)内部点扩散算法
该算法由每个多边形的一个内部点(也叫种子点)开始,向其八个方向的领点扩散,判断各个新加入的点是否在多边形的边界上,如果是在多边形的边界上,则该新加入的点不作为种子点,否则把非边界的领点作为新的种子点与原有种子点一起进行新的扩散运算。一般来说,由于扩散算法比较复杂,并且在一定的栅格精度上,如果复杂图形的同一多边形的两条边界落在同一个或相邻的两个栅格内,会造成多边形不连通,这样一个种子点就不能完成填充

2)射线算法
射线算法就是通过判断数据栅格点是否在多边形内部,如果在内,则填充,在外则不填充。至于怎么判断,在之前的《GIS算法基础(二)计算几何基础(中)》已经对判断点是否在多边形内的两种算法进行了实现。
二、射线算法的实现
算法的基本思想就是通过计算每个栅格点是否在多边形内部,然后决定是否填充。
算法步骤:
①对多边形边界进行栅格化(线状要素的栅格化---GIS算法基础(五)中已经实现)
②遍历栅格像元,判断是否在多边形内部(判断点在多边形内部算法--GIS算法基础(二)计算几何基础(中)中已经实现)
③渲染处理
其实在②中也可以进行一个最小包围盒的获取,然后只需要遍历这个包围盒范围的栅格即可,不过为了简单起见,我的实现就遍历整个栅格像元(30x30其实也不大哈哈)
//矢量化多边形(用射线法或转角法填充面,用八方向栅格化或全路径栅格化填充边界)
/**
*
* @param polygon
* @param RasterType 0-八方向栅格化 1-全路径栅格化
* @param type 0-射线法 1-转角法
*/
public void RasterPolygon1(Polygon polygon,int RasterType,int type) {
RasterLine(polygon, RasterType);
for(int i=0;i<=ROW;i++) {
for(int j=0;j<=COLUMN;j++) {
//count++;
//System.out.println(String.format("%d %d", i,j));
if(CalculateBasic.isPointAtPolygon(polygon, transformVetorPoint(i, j, 0, 0), type)) {
setValue(i, j);
}
}
}
//System.out.println("counter "+count);
}这里的transformVetorPoint是栅格点转矢量点。
在由栅格点判断是否在多边形内部中的时候,由于栅格点是栅格像元,而多边形是矢量要素,不能进行直接的关系判断,因此需要进行转换,把栅格点转为矢量点。
之前矢量点转栅格点的公式:

那么栅格点转矢量点就是逆着来:
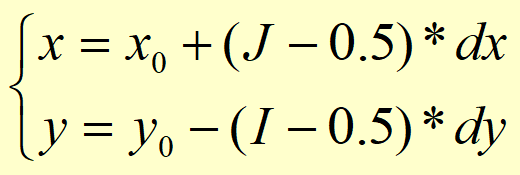
x0,y0代表栅格的坐标原点在直角坐标系中的坐标,dx,dy分别代表矩形栅格的长和宽
transformVetorPoint代码实现:
/**
* 求出的坐标是栅格的中心点
* @param row 行
* @param colum 列
* @param xOffset 起始栅格点的x位移量
* @param yOffset 起始栅格点的y位移量
* @return
*/
public Point transformVetorPoint(int row,int colum,double xOffset,double yOffset) {
double x0=size+xOffset+this.xOffset;//栅格起始点坐标
double y0=ROW+yOffset+this.yOffset;
double x = x0+(colum-0.5)*size;
double y = y0-(row-0.5)*size;
Point newPoint=new Point(x, y);
// newPoint = BasicTransform.transform(newPoint, ROW/2, COLUMN/2);
return newPoint;
}
三、测试结果:
输入数据:
o=new Point(3,9);
d=new Point(9,3);
e=new Point(18,18);
r=new Point(12,18);
t=new Point(21,3);
y=new Point(27,9);
q=new Point(15, 30);
Point[] points = new Point[] {o,d,e,r,t,y,q};
Polygon polygon = new Polygon(points,true);GUI绘制(矢量要素绘制,绘制实现在github上):
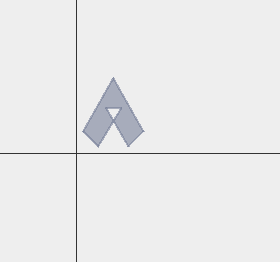
输出结果(控制台输出):



