GIS算法基础(八)基于距离变换的栅格骨架提取算法
一、为什么需要骨架提取
简单来说就是用于细化栅格,便于栅格数据转换为矢量数据
栅格格式向矢量格式转换是提取相同编号的栅格集合表示的边界,栅格点转换成矢量点,很简单,在坐标系确定的情况下通过解析式可以直接转换。而线与面在转换成矢量的时候,本质上都是在提取边界或中轴线,因此在栅格中提取中轴线就与栅格的细化的关系密不可分,这是因为线状栅格数据一般具有粗度且线条本身往往呈现粗细。栅格数据需要细化,以提取中轴线。这是因为:
①中轴线是栅格数据曲线的标准化存储形式
②实现细化是将栅格曲线矢量化的前提
③在有些算法中可以提高计算精度
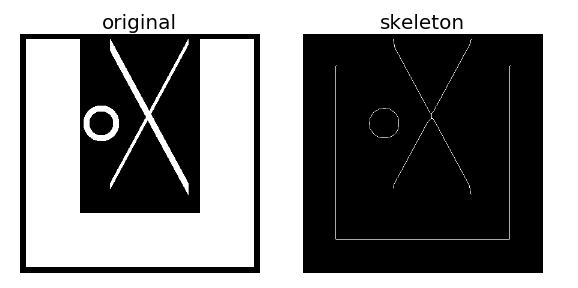
二、距离变换法提取骨架
距离变换图
距离变换图也是一种栅格图像,其中,每个像元值存储了它到栅格图上相邻物体的最近距离。这个距离的量度:可以是曼哈顿距离,棋盘距离,或者欧式距离。这三个距离关系在GIS中很常用。算法实现如下:
/**
*
* @param disType 距离类型
* @param s1 像元1
* @param s2 像元2
* @return
*/
private double calculateDis(DisType disType,Pixel s1,Pixel s2) {
double dis = 0;
switch (disType) {
case Euclidean:
dis = Math.sqrt(Math.pow(s1.getRow()-s2.getRow(), 2)+Math.pow(s1.getColumn()-s2.getColumn(), 2))*size;
break;
case CityBlock:
dis = Math.abs(s1.getRow()-s2.getRow())+Math.abs(s1.getColumn()-s2.getColumn())*size;
break;
case ChessBoard:
dis = Math.max(Math.abs(s1.getRow()-s2.getRow()), Math.abs(s1.getColumn()-s2.getColumn()))*size;
break;
default:
dis = Math.sqrt(Math.pow(s1.getRow()-s2.getRow(), 2)+Math.pow(s1.getColumn()-s2.getColumn(), 2))*size;
break;
}
return dis;
}
基于距离变换法提取骨架算法思想:
对内部点集i到非内部点集e(孤立点与边界点)求最小距离,实际上就是求目标点到最近背景点的距离(背景点-值为0的像元 目标点-值为1的像元),求出距离后 对距离进行分类即可得骨架图
基于距离变换法提取骨架算法步骤:
①将栅格图像进行初始二值化(背景点设为0,目标点设为1)
②将栅格图像进行分类,把栅格分为内部点,边界点,孤立点。
③求每一个内部点到非内部点的距离,距离值赋给栅格值
④对栅格图像进行二值化(距离大于1的栅格值设为1,小于等于1的设为0)
③重复②③④,终止条件为“若下一次栅格图像二值化结果全部为0”
如何分类:
在步骤②中,如何把栅格分为内部点,边界点,孤立点?
以中心像素的四邻域为例,
1、如果中心像素为目标像素(值为1)且四邻域都为目标像素(值为1),则该点为内部点。
2、如果该中心像素为目标像素,四邻域为背景像素(值为0),则该中心点为孤立点。
3、其他情况则为边界点
分类代码实现
//判断是边界点,内部点,孤立点
//前提:栅格已经二值化
public void setNeighbourhood() {
internalPoints = new ArrayList<>();
borderPoints = new ArrayList<>();
for(int i=0;i<ROW;i++) {
for(int j=0;j<COLUMN;j++) {
//假-0 真-1
boolean up=true,down=true,right=true,left=true;
//判断点的上部是否为0
try {
if(data[i-1][j].getValue()==0) {
up=false;
}
} catch (Exception e) {
// TODO: handle exception
up=false;
}
//判断点的下部是否为0
try {
if(data[i+1][j].getValue()==0) {
down=false;
}
} catch (Exception e) {
// TODO: handle exception
down=false;
}
//判断点的左边是否为0
try {
if(data[i][j-1].getValue()==0) {
left=false;
}
} catch (Exception e) {
// TODO: handle exception
left=false;
}
//判断点的右边是否为0
try {
if(data[i][j+1].getValue()==0) {
right=false;
}
} catch (Exception e) {
// TODO: handle exception
right=false;
}
if(!up && !down && !left && !right) {
data[i][j].setType(type.isolated);
}else if(up && down && left && right) {
data[i][j].setType(type.internal);
internalPoints.add(data[i][j]);
}else {
data[i][j].setType(type.boundary);
borderPoints.add(data[i][j]);
}
}
}
}测试结果:
B代表边界点,I代表内部点,孤立点未进行渲染
基于距离变换法提取骨架算法实现
我使用了3*3模板的快速距离变换。
按照从上到下,从左到右的顺序,遍历3x3的栅格图像
但是有个问题是:如果在遍历过程中,碰到了栅格的边界怎么办,所以我写了对应的解决办法,即先确定快速距离变换遍历的范围,在开始遍历快速距离变换。
代码如下:
/**
* 骨架图算法(距离变换法搜索中轴线)
* 对内部点集i到边界点集e求最小距离
* 实际上就是求目标点到最近背景点的距离
* 背景点-值为0的像元 目标点-值为1的像元
* 求出距离后 对距离进行分类即可得骨架图
*/
public void getMinDis(DisType disType) {
//快速距离模板计算
//从左至右,从上到下,顺时针寻找周围是否有边界点
//如果有,则加入计算
//如果没有,则扩大搜寻范围,最大范围到数组越界
//最后得出最小距离
//当前圈层数
if(borderPoints==null && internalPoints==null) {
setNeighbourhood();
}
for(Pixel i:internalPoints) {
List<Double> disList = new ArrayList<>();
//搜索范围
int cicleNum = 1;
//上下左右搜寻边界
int up,down,left,right;
int upLimit,downLimt,leftLimit,rightLimit;
upLimit = 1;
downLimt = ROW;
leftLimit = 1;
rightLimit = COLUMN;
//确定遍历范围,防止边界溢出
for(int curCir=0;curCir<cicleNum;curCir++) {
try {
up = i.getRow()-cicleNum;
if(up<upLimit) {
up=upLimit;
}
} catch (Exception e) {
// TODO: handle exception
up = i.getRow();
}
try {
down = i.getRow()+cicleNum;
if(down>downLimt) {
down = downLimt;
}
} catch (Exception e) {
// TODO: handle exception
down = i.getRow();
}
try {
left = i.getColumn()-cicleNum;
if(left<leftLimit) {
left = leftLimit;
}
} catch (Exception e) {
// TODO: handle exception
left = i.getColumn();
}
try {
right = i.getColumn()+cicleNum;
if(right>rightLimit) {
right=rightLimit;
}
} catch (Exception e) {
// TODO: handle exception
right = i.getColumn();
}
//记录栅格周边是否有非内部点,没有的话则圈数+1
boolean flag = false;
//从最左最上开始遍历,遍历顺序从左至右,从上到下
for(int row=up;row<down;row++) {
for(int col=left;col<right;col++) {
//判断是否为中心点,即i点,是就跳过
if(row==i.getRow() && col==i.getColumn()) {
continue;
}
//判断是否是内部点,如果是内部点就直接跳过
if(data[row][col].getType()!=type.internal) {
flag = true;
//计算最小距离
double dis = calculateDis(disType, i, data[row][col]);
disList.add(dis);
}
}
}
//当前圈数内未发现非内部点
if(!flag) {
cicleNum++;
}else {
//已经发现了非内部点,循环结束
break;
}
}
//当前栅格搜索完毕,获取到最近非内部点的距离
if(!disList.isEmpty()) {
double min = Collections.min(disList);
i.setNearDis(min);
}
}
}测试结果:
原始数据:

距离变换细化一次:

距离变换细化2次

。。。
n次








