GIS算法基础(十)矢量压缩算法-光栏法
前言:
远程仓库地址:https://github.com/XiaoZhong233/GIS_ALG
光栏法是一种矢量数据的压缩算法。光栏法的基本思路是对每一条曲线上的所有点, 逐点定义一个扇形区域。若曲线的下一节点在扇形外, 则保留当前节点; 若曲线的下一节点在扇形内, 则舍去当前节点。
说明:
光栏法与道格拉斯算法都是矢量压缩算法,但是光栏法能很好的保存线的形状,而道格拉斯普克算法是概化算法,他的作用主要是把凹凸不平的折线变得平直,因此算“概化”算法
算法步骤:

1、输入光栏的口径d
这个口径也就是每次扫描的扇形区域,若曲线的下一节点在扇形外, 则保留当前节点; 若曲线的下一节点在扇形内, 则舍去当前节点。
2、读取坐标
1、2两点坐标,记入p1,p2
3、建立光栏
连接p1和p2点,过 p2点作一条垂直于p1p2 的直线,在该垂线上取 两点a1和a2,使a1p2= a2p2=d/2,此时a1和 a2为“光栏”边界点, p1与a1、p1与a2的连线 为以p1为顶点的扇形的 两条边,这就定义了一 个扇形(这个扇形的口朝 向曲线的前进方向,边 长是任意的)。通过p1并在扇形内的所有直线都具有这种性质, 即p1p2上各点到这些直线的垂距都不大于d/2。
若p3点在扇形内,则舍去p2点。然后连接p1和p3,过p3作 p1p1的垂线,该垂线与前面定义的扇形边交于c1和c2。在垂线 上找到b1和b2点,使p3b1=p3b2=d/2,若b1或b2点落在原扇 形外面,则用c1或c2取代。此时用p1b1和p1c2定义一个新的扇 形,这当然是口径(b1c2)缩小了的“光栏”。
4、检查下一节点
若该点在新扇形内,则重复第(2)步;直 到发现有一个节点在最新定义的扇形外为止。
当发现在扇形外的节点,如p4,此时保留p3点,以p3作为 新起点,重复1°~3°。如此继续下去,直到整个点列检测完 为止。所有被保留的节点(含首、末点),顺序地构成了简化后 的新点列。

实现代码:
1 /** 2 * 光栏法压缩折线 3 * @param caliber 口径 4 * @return 5 */ 6 public Polyline simplify_LightBar(double caliber) { 7 if(caliber<=0) 8 return null; 9 if(this.points.size()<2) { 10 return this; 11 } 12 //求光栏下边界 13 List<Point> points = this.getPoints(); 14 Point p1 = points.get(0); 15 Point p2 = points.get(1); 16 Line line = new Line(p1,p2); 17 double len = line.getLength(); 18 double angle1 = Math.toDegrees(Math.atan2(.5*caliber,len)); 19 double angle2 = line.getVector2D().getAngle(); 20 21 //求光栏下边界 22 Line down = new Line(angle2-angle1, p1); 23 //求光栏上边界 24 Line up = new Line(angle1+angle2,p1); 25 26 27 // //计算光栏a1,a2坐标 28 // //p1p2直线的法线矢量 29 // Vector2D n = line.getN(); 30 // //光栏垂直平分线的垂线 31 // Line l = new Line(n,p2); 32 // Point a1 = l.intercourse(down); 33 // Point a2 = l.intercourse(up); 34 for(int i=2;i<points.size();i++) { 35 Point p = points.get(i); 36 //如果下一个点在光栏内,则删除上一个点,当前点为新p2 37 //如果不在,则保留上一个点,以上一个点为新p1 38 if(isInLightBar(up, down, p)) { 39 points.get(i-1).setEnable(false); 40 p2=p; 41 //求当前点与p1的垂线 42 Line line2 = new Line(p1,p2); 43 Vector2D nn = line.getN(); 44 Line line3 = new Line(nn,p); 45 //建立新的光栏 46 double length = line2.getLength(); 47 double angle11 = Math.toDegrees(Math.atan(.5*caliber/length)); 48 double angle22 = line2.getVector2D().getAngle(); 49 Line newDown = new Line(angle22-angle11, p1); 50 Line newUp = new Line(angle11+angle22,p1); 51 //求当前点与p1的连线的垂线与新光栏的交点 52 Point b1 = line3.intercourse(newDown); 53 Point b2 = line3.intercourse(newUp); 54 //检查新光栏的交点是否在原光栏内 55 //如果在就使用新光栏,不在就构建另一个光栏 56 if(isInLightBar(up, down, b1) && isInLightBar(up, down, b2)) { 57 down = newDown; 58 up = newUp; 59 }else { 60 //只有b1在光栏内 61 if(isInLightBar(up, down, b1)) { 62 down = new Line(p1,b1); 63 } 64 if(isInLightBar(up, down, b2)) { 65 up = new Line(p1,b2); 66 } 67 } 68 69 }else { 70 points.get(i-1).setEnable(true); 71 p1=points.get(i-1); 72 p2=points.get(i); 73 line = new Line(p1,p2); 74 len = line.getLength(); 75 angle1 = Math.toDegrees(Math.atan(.5*caliber/len)); 76 angle2 = line.getVector2D().getAngle(); 77 //求光栏上下边界 78 down = new Line(angle2-angle1, p1); 79 up = new Line(angle1+angle2,p1); 80 } 81 82 83 84 } 85 86 List<Point> selectedPoints = new ArrayList<>(); 87 Collections.addAll(selectedPoints, new Point[this.points.size()]); 88 Collections.copy(selectedPoints, this.points); 89 Iterator<Point> iterator = selectedPoints.iterator(); 90 while (iterator.hasNext()) { 91 Point point = (Point) iterator.next(); 92 if(!point.isEnable()) { 93 iterator.remove(); 94 } 95 } 96 97 return new Polyline(selectedPoints); 98 } 99 /** 100 * 判断点是否光栏内 101 * @param up 102 * @param down 103 * @param point 104 * @return 105 */ 106 private static boolean isInLightBar(Line up,Line down,Point point) { 107 Point start = up.getStart(); 108 Line line = new Line(start,point); 109 Vector2D upVector = up.getVector2D(); 110 Vector2D downVector = down.getVector2D(); 111 Vector2D target = line.getVector2D(); 112 //利用矢量的叉积判断即可 113 if(target.crossProduct(upVector)>=0 && target.crossProduct(downVector) <=0) { 114 return true; 115 } 116 return false; 117 }
运行结果:
原始数据:

光栏法压缩后(阈值5)

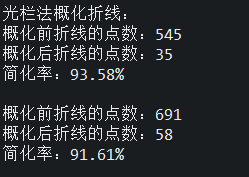
因为有两条折线,所以概化了两次
再次使用光栏法压缩(阈值调为10)

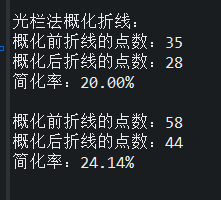
再次使用光栏法压缩(阈值调为20)


再次使用光栏法压缩(阈值调为50)

总结
与道格拉斯算法的对比:
道格拉斯普克算法采用递归实现,它需要对整条曲线进行扫描,才能进行压缩,而且采用递归,计算量较大。
光栏法能给定阈值保留曲线特征点、并且他和道克拉斯普克算法最大的不同是,他能实时计算的,且计算量较小,占用的内存也小了。
因此光栏法是一种优秀高效的矢量压缩算法


