CBT

1. 设置扬声器阵列，预先设置扬声器阵列的覆盖角
2. 根据扬声器阵列的覆盖角得到截止频率F
3. 将音频信号小于截止频率F的频段采用空间重采样法进行恒定束宽控制；将音频信号大于或等于截止频率F的频段采用CBT阵列理论进行恒定束宽控制；

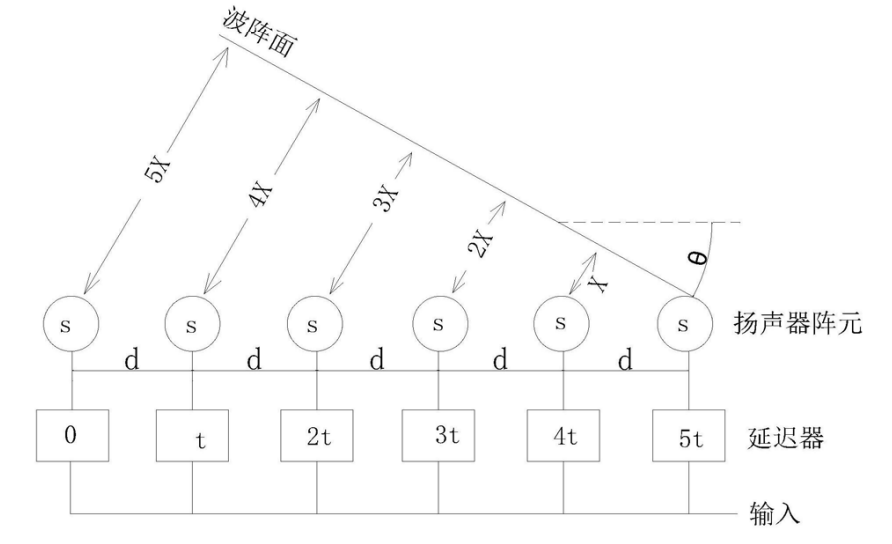
基本流程图如下：

step1: 首先，确定系统参数. 根据期望的\(\theta\)，结合实际的手中已有的条件、资源等（如考虑到阵元的size以及Number涉及到钱的问题），折中确定好阵列的间距，也就确定了阵列的长度
如阵列间距为17mm, 50个阵元, 则具体计算公式为:
\(f_{下限} = \frac{声速}{阵列长度} = \frac{343}{(50-1)17*10^{-3}} = 417\)Hz
\(f_{上限} = \frac{声速}{阵元间距} = \frac{343}{17*10^{-3}} = 20200\)Hz
当驱动器间距等于一个波长时，出现波束宽度控制的频率上限，而当驱动器间距大于半个波长时，可能开始形成旁瓣。因此，即使具有换能器102(或驱动器)的阵列150可间隔开17mm，阵列150也可提供高达20200Hz下的恒定波束宽度，在10 ,100Hz处开始形成旁瓣。

step2: 然后, 衍生虚拟圆弧. 通过延时来虚拟地“弯曲”这个线性的阵列，以实现beamwidth.
具体做法如下：

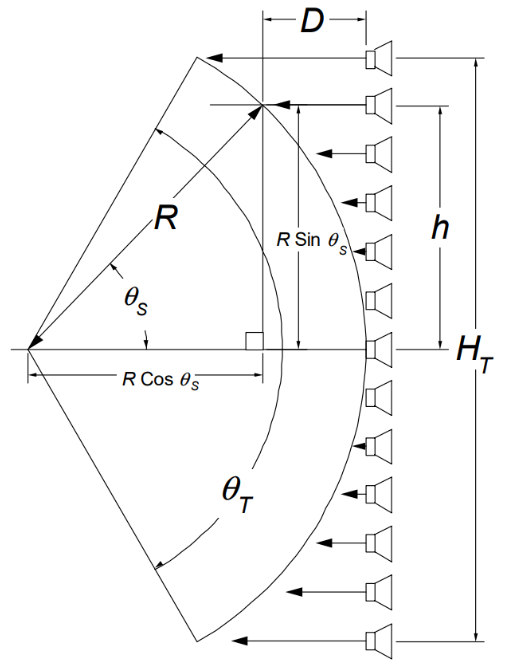
step1：对各阵列进行不同程度的时间延迟，进而产生虚拟圆弧
进一步做法如下：
确定好的beamwidth是整个圆弧角对应的范围，即图中的\(\theta_T\), 弧角的一半即半角为\(\theta_0\)

将每个阵元向后移动到弧上，水平移动，注意这里移动到弧上之后的阵元间距即每段弧长是不等的。

然后根据图中的几何关系，确定好每个阵元具体相对于圆弧中心的角度\(\theta_S\)
具体公式为

\[U(x)= \begin{cases} 1+0.066x - 1.8x^2 + 0.734x^3 &, x\leq 1 \\ 0 &, x\ge 1 \end{cases} \]

其中，这里的\(x = \frac{\theta}{\theta_0}\)

CBT圆弧的半径计算方式为:

\[R= \frac{H_t}{2\sin(\frac{\theta_t}{2})} = \frac{H_t}{2\sin(\theta_0)} \]

从直线阵向后移动到弧上的各阵元的角定位的计算方式为:

\[\theta_S = \arcsin(\frac{h}{R}) \]

其中, \(h\)是各阵元的高度.

进一步, 从直线阵水平后移到圆弧阵所需的偏移量的计算方式为:

\[D = R(1-\cos(\theta_S)) \]

知道了各个阵元的偏移量, 也就确定了各阵元具体所需的延时\(\tau\)

\[\tau = D/C \]

至此, 完成了从直线阵到虚拟圆弧阵的转换, 但此时还是单一方向的, 暂无偏转.

step3: 波束指向中心进行偏转
二维旋转矩阵逆时针:

\[\begin{bmatrix} \cos(\alpha) & -\sin(\alpha) \\ sin(\alpha) & \cos(\alpha) \end{bmatrix} \]

二维旋转矩阵顺时针:

\[\begin{bmatrix} \cos(\alpha) & \sin(\alpha) \\ -sin(\alpha) & \cos(\alpha) \end{bmatrix} \]

可能有所疑问, 为何这就是旋转了? 具体可以这么看:

\[V \cdot A = \begin{bmatrix} \cos(\alpha) & -\sin(\alpha) \\ \sin(\alpha) & \cos(\alpha) \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x\cos(\alpha)-y\sin(\alpha) \\ y\sin(\alpha)+y\cos(\alpha) \end{bmatrix} \]

而

\[A = \begin{bmatrix} r\sin(\theta) \\ r\sin(\theta) \end{bmatrix} \]

所以

\[\begin{align*} x &= r \cos(\theta) \\ y &= r \sin(\theta) \\ \end{align*} \]

\[\begin{align*} x &= r \cos(\theta) \\ y &= r \sin(\theta) \\ \cos(\theta + \alpha) &= \cos(\theta)\cos(\alpha) - \sin(\theta)\sin(\alpha) \\ \sin(\theta + \alpha) &= \sin(\theta)\cos(\alpha) + \cos(\theta)\sin(\alpha) \end{align*} \]

所以, \(V\)是一个旋转矩阵.

step4:
相乘完成线阵的偏转, 然后归一, 因为可能会涉及到延迟 和 提前. 没办法提前, 所以, 进行一个类似归一化的操作, 令提前的为0, 然后延迟的再延迟即可.

最后就是权重和相移相乘 $ \omega e^{-j2\pi f\tau} $

然后fft后的数据和这个相乘的结果就是最终的波束数据, 此时, 再将结果进行ifft, 转换到时域.