KMP模式匹配算法
在讲KMP模式匹配算法之前,先来讲讲朴素的模式匹配算法:
朴素的模式匹配算法:
假设现在有一个母串 S=“GoodGoogle"和一个子串T = “Google”,要在母串中找到子串的位置(首字符位置)。那么可以这样做:从S和T的首字符开始遍历,如果首字符相等,就进而比较第二个字符,第二个字符相等,就比较第三个字符......直到成功在母串找到子串(一次成功),或者因为某个字符不同而中断。
从首字符开始直接成功找到子串自然不必多说(这是最理想的状况)。来说说因为字符不同而中断的情况:
母串S = “GoodGoogle”,字串T = “Google",显然,在字符串下标为3(第四个字符)的地方,‘d’ 和 ‘g’ 不同,这个时候就要中断比较。中断之后呢? 就从母串S的第二个字符开始比较(和字串的首字符开始比较,也就是‘ o '和’ G '),直到比较的字符不同为止,继而换母串的第三个字符,继续同字串的第一个字符开始比较起来,如此反复,就能找到字串在母串中的位置。
总结一下:对母串的每一个字符作为字串的开头,与要匹配的字符串进行匹配。对母串做大循环,每个字符开头做子串的小循环,直到匹配成功或者全部遍历完(即未找到)。
源代码大致如下:
1 int Index(char S[], char T[]) 2 { 3 int i = 0, j = 0; //下标从1开始,下标为0的字符用空格代替,不计 4 int lenS = strlen(S) - 1; 5 int lenT = strlen(T) - 1; 6 7 while (i <= lenS && j <= lenT) 8 { 9 if (S[i] == T[j] 10 { 11 ++i; 12 ++j; 13 } 14 else 15 { 16 i = i - (j - 1) + 1; 17 j = 0; //i下移一位,j回到子串开头。 18 } 19 if (j > lenT) //也就是说匹配成功 20 reutrn i - lenT; //返回匹配字串的首字符地址 21 else 22 return 0; //匹配失败 23 }
这个算法的优缺点都很明显,优点显然是易于理解,而缺点即是时间复杂度: (假设字串为m,母串为n),那么最坏的情况是每次遍历都在最后一个不等,直到母串的最后一个元素,也就是说,每次最多比较m次,最多比较(n - m + 1)次。那么时间复杂度也就是O(m * ( n - m + 1)),也就是平方阶。这样的话在比较大量字符串的时候这个算法也就无卵用了。
且不论我们能不能忍受这个低效的算法。对于科学家们来说这是无法忍受的,于是,D.E.Knuth J.H.Morris V.R.Pratt三人便发明了一个模式匹配的算法,也就是KMP算法。
KMP算法:(我想吐槽一下这玩意儿理解起来真难)
利用已经部分匹配这个有效信息,保持i指针不回溯,通过修改j指针,让母串尽量地移动到有效的位置。
嘛 ,听我慢慢说来。
假设现在有一个母串“abcdefgab" 以及一个子串" abcdex",假设i指针指向母串首字符,j指针指向字串首字符。
接下来,按照前面介绍的模式朴素匹配算法,一个一个进行比较。但是,仔细观察,你会发现,子串"abcdex"的首字母”a"与它后面的"bcdex"都不相同,而子串与母串的前面五位都相同(相匹配),这也就是说,子串的"a"不可能和母串的第二到第五位(也就是”bcde")相同,这样的话,我们就可以把模式朴素匹配算法省略一部分(也就是子串的首字符和母串的第二到第五个字符不用比较,比较了也是白费劲)。
如此一来,i的指针就没有了回溯的必要了(在模式朴素匹配算法里面经常要回溯)。需要回溯的就只有j指针,也就是指向子串的指针。
所以,整个KMP的重点就在于当子串的某一个字符与母串不匹配时,j指针要移动到哪儿?
那么接下来我们就来发现一下子串的 j 指针的移动规律。
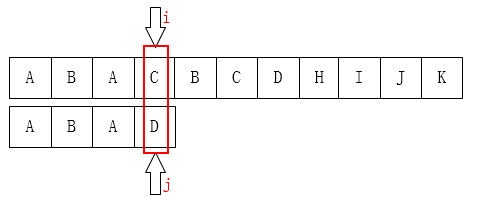
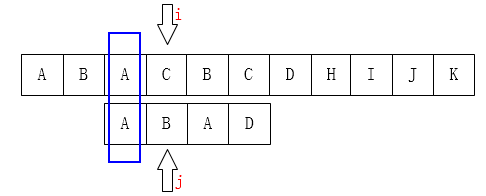
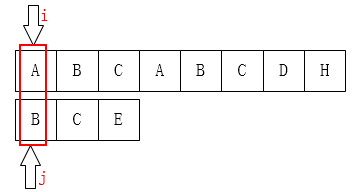
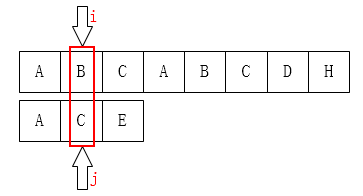
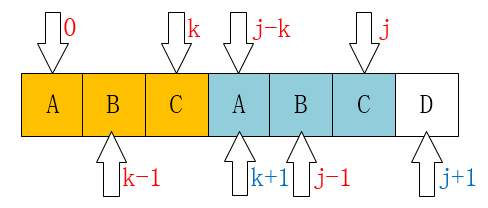
如左上图:C 和 D不匹配了,我们要把j移动到哪儿? 显然是第二位(B),为什么呢? 因为在子串中 ,D前面的A和子串的第一个字符A一样。移动结果如右上图。
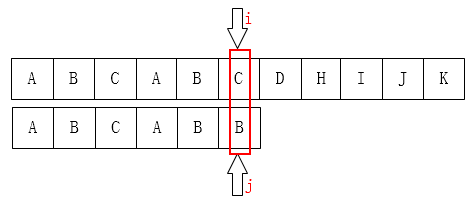
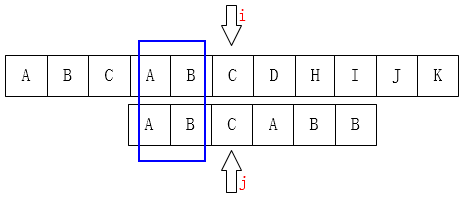
再看一组图:C和B不匹配,我们可以把指针移动到第三位C
这样的话,我们就可以看出来点什么了:j 要移动的下一个位置k存在着这样的性质:k之前(0 ~ k - 1)的元素和 j 之前(j - k ~ j - 1)的元素相同(实际上,符合条件的k不止一个)。
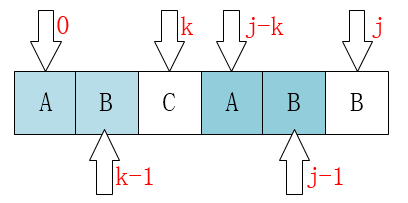
那么现在问题又来了,怎么求这个k?
因为在每一个位置都可能发生不匹配,因此我们要计算每一个位置所对应的k值,也就是说我们需要一个数组来存放k,假设这个数组名为next,那么就有 next[j] = k; 即把k 的值赋值个对应的j,表示当母串[i] != 子串[j]时(即母串和子串不匹配的时候),j指针指向的下一个位置(也就是k)。
实现next的源代码如下:
1 void get_next(char T[], int *next) 2 { 3 int k = -1, j = 0; 4 next[0] = -1; 5 while (j < lenT) // lenT = strlen(T) - 1 6 { 7 if (k == -1 || T[j] == T[k]) 8 { 9 next[++j] = ++k; 10 } 11 else 12 k = next[k]; 13 } 14 }
这个源代码看起来很简单,实际上理解起来有难度(我tm困在这个半天)。
当j = 0的时候,如果不匹配,此时j 不可能再向左(向前)回溯,只能由i 向右移动一位,因此,next[0] = -1。
而当j = 1时,j 就只能移动到前面(也就是第一个元素的位置了)
 、
、
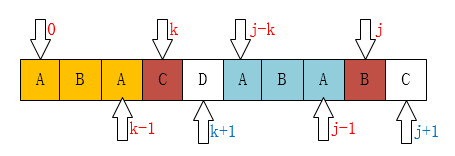
接着就是当 j > 1时 了。仔细观察上面两个图,会发现一些规律: 当T[k] == T[j]时,有next[j + 1] == next[j] + 1。
而这个规律,也可以证明:已知 next[j] == k; 即 T[ 0 ~ k - 1] == T[j - k ~ j - 1];
又因为T[k] = =T[j];
所以 T[0 ~ k - 1] + T[k] == T[j - k ~ j - 1] + T[j] ,即T[0 ~ k] == T[j - k ~ k]
从而可得 next[++j] == next[j] + 1 == ++k;
这也就是上面的if语句块的公式的由来。
而当T[k] != T[j]时,又该怎么办呢? 直接使用上面的next[++j] = ++k肯定是不行的,因为当T[k] != T[j] 的时候 不可能存在T[0 ~ k] == T[j - k ~ k]。
那么这时候,我们可以通过缩小k的范围,使得彼时的k 满足 T[k] == T[j] ——也就是T[0 ~k] == T[j - k ~ k]。
具体要怎么做呢?怎样缩小k的范围?
答案也很简单,对k做递归运算就好了。
我们可以把 (j - k ~ j )的这个范围作为母串,把(0 ~ k)范围作为子串,进行一次KMP匹配。
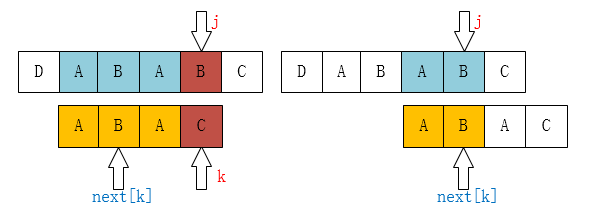
如上图,进行了一次kmp匹配之后,k = next[k] (递归调用) ,这个时候我们就会发现出现 T[next[k]] == T[j]这个条件了(next[k] == k)。这样子,也就把未知的东西转化成已知的了。
这样一来,获取子串T的next数组也就搞定了,接下来是KMP算法本身(调用next数组)。
int Index_KMP(char S[], char T[], int pos) { int i = 0; j = 0; //i用于母串,j用于子串 int next[255]; get_next(T, next); //得到next数组 while (i <= strlen(S) - 1 && j <= strlen(T) - 1) { if (j == -1 || S[i] == T[j]) //俩字母相等则继续,而j == -1 则是用于一开始就不匹配的情况 { ++i; ++j; } else { j = next[j]; //j 退回合适的位置,也就是get_next()里面k的位置,而i不需要回溯 } } if (j > strlen(T) - 1) return i - (strlen(T) - 1); else return 0; }
分析一下上面的代码:代码和朴素的匹配模式算法相比,改动不多,关键就是去掉了i 值回溯的部分以及把j 退回到合适的位置(而不是j = 0)。而我们比较关心的是代码的复杂度,这个才是最重要的,平方阶的代码无卵用。
假设子串T的长度为m,母串的长度为n,那么get_next()函数的复杂度为O(m),而Index_KMP的复杂度是O(n) 。总的时间复杂度应该就是O( m + n), 也就是说是线性的。(nice)
整个KMP大致就是这样了,但实际上.................还没完,这个算法还存在缺陷。
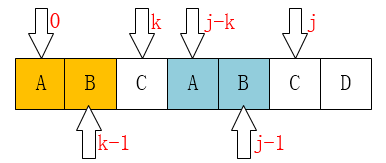
我举个栗子:
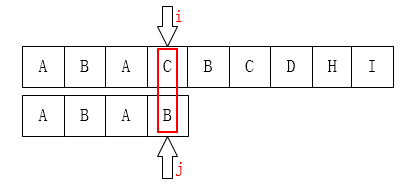
显然,由上面的get_next()函数得到的next数组应该是 [ -1, 0, 0, 1],那么j就应该移动到第二个字符的位置(下标为1)。 如下图:

问题就出在这里了,看上图,这一步是没有意义的,后面的B是不匹配的,那么前面的B也不匹配。那么原因在于哪里呢?
很容易看出,问题出现在不应该有T[ j ] == T [ next [j] ],为什么?
假设母串是S,那么当S [ i ] != T[ j ] 的时候,j 会调到下一个位置,也就是 next[ j ],那么,如果j == next[ j ] 的话,那么这个步骤就毫无意义(重复了)。
解决办法也很简单,就是将本来的next[ j ] = k 中的k 再次递归,变成next [ k ]。直到不重复为止。
void get_next(char T[], int *next) { int j = 0, k = -1; next[0] = -1; while (j < strlen(T) - 1) { if (k == -1 || T[j] == T[k]) { if (T[++j] == T[++k] //如果相等,那么就不要用next[j] = k这一步骤,而是跳过,使用next[k]来找到更小的。 { next[j] = next[k]; } else next[j] = k; } else k = next[k]; } }
这样子,KMP的缺陷就搞定了。
-_-
总算搞定了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号