边缘碰撞检测
边缘碰撞检测
粗碰撞检测
包围盒形式
外接圆碰撞检测
这个方法比较直观,多边形外接圆圆心距离大于两者的半径和即可( d>R1+R2 )

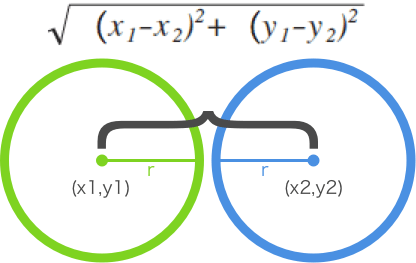
Math.sqrt(Math.pow(circleA.x - circleB.x, 2) +
Math.pow(circleA.y - circleB.y, 2))
< circleA.radius + circleB.radius
在线运行示例:
http://codepen.io/JChehe/pen/EZrorG
为了尽可能表示车辆所占用的面积,又尽量减少自由空间的侵占,在一些paper中常会看到用多个圆来包络车辆

优点:易于实现,算法计算量小
缺点:会侵占可行驶区域,造成自由空间狭窄。
AABB(Axis Aligned Bounding Box)
AABB矩形框与AABB矩形框
AABB方法使用与坐标轴平行的外接矩形来分析两个物体之间的碰撞关系,只需要比较两个矩形的上下、左右边的大小即可,非常轻便。但是忽略了物体的旋姿态,会丢失掉一部分自由区域,适合进行粗略的碰撞检测

GLboolean CheckCollision(GameObject &one, GameObject &two) // AABB - AABB collision
{
// x轴方向碰撞?
bool collisionX = one.Position.x + one.Size.x >= two.Position.x &&
two.Position.x + two.Size.x >= one.Position.x;
// y轴方向碰撞?
bool collisionY = one.Position.y + one.Size.y >= two.Position.y &&
two.Position.y + two.Size.y >= one.Position.y;
// 只有两个轴向都有碰撞时才碰撞
return collisionX && collisionY;
}
在线运行示例:
在线运行示例(先点击运行示例以获取焦点,下同): See the Pen AxisAlignedBoundingBox collision detection
圆框与AABB矩形框(矩形框不旋转)
解决方式一:
检测圆和AABB碰撞的算法会稍稍复杂,关键点如下:我们会找到AABB上距离圆最近的一个点,如果圆到这一点的距离小于它的半径,那么就产生了碰撞。
难点:在于获取AABB上的最近点。
下图展示了对于任意的AABB和圆我们如何计算该点:
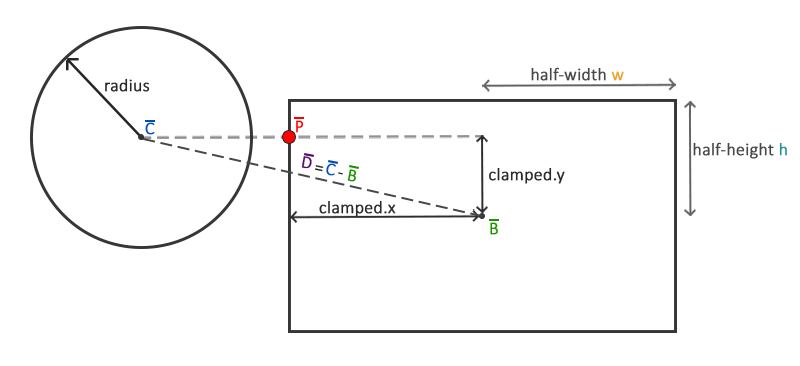
第一步:首先我们要获取球心与AABB中心的矢量差。
第二步:接下来用AABB的半边长(half-extents)和来限制(clamp)矢量。长方形的半边长是指长方形的中心到它的边的距离;简单的说就是它的尺寸除以2。这一过程返回的是一个总是位于AABB的边上的位置矢量(除非圆心在AABB内部)。
限制运算把一个值限制在给定范围内,并返回限制后的值。通常可以表示为:
float clamp(float value, float min, float max) {
return std::max(min, std::min(max, value));
}
例如,值42.0f被限制到6.0f和3.0f之间会得到6.0f;而4.20f会被限制为4.20f。
限制一个2D的矢量表示将其x和y分量都限制在给定的范围内。
这个限制后矢量+AABB框图的中心就是AABB上距离圆最近的点的坐标。接下来我们需要做的就是计算一个新的差矢量,它是圆心和的差矢量。
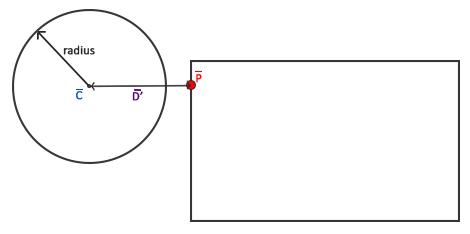
第三步:根据最近点p与圆心之间的矢量摸长与圆的半径进行对比,判断是否发生碰撞
GLboolean CheckCollision(BallObject &one, GameObject &two) // AABB - Circle collision
{
// 第一步:
// 获取圆的中心
glm::vec2 center(one.Position + one.Radius);
// 计算AABB的信息(中心、半边长)
glm::vec2 aabb_half_extents(two.Size.x / 2, two.Size.y / 2);
glm::vec2 aabb_center(
two.Position.x + aabb_half_extents.x,
two.Position.y + aabb_half_extents.y
);
// 第二步
// 获取两个中心的差矢量
glm::vec2 difference = center - aabb_center;
glm::vec2 clamped = glm::clamp(difference, -aabb_half_extents, aabb_half_extents);
// AABB_center加上clamped这样就得到了碰撞箱上距离圆最近的点closest
glm::vec2 closest = aabb_center + clamped;
// 第三步:
// 获得圆心center和最近点closest的矢量并判断是否 length <= radius
difference = closest - center;
return glm::length(difference) < one.Radius;
}
解决方式二:
如何找出矩形上离圆心最近的点呢?下面我们从 x 轴、y 轴两个方向分别进行寻找。为了方便描述,我们先约定以下变量:
矩形上离圆心最近的点为变量:closestPoint = {x, y};
矩形 rect = {x, y, w, h}; // 左上角与宽高
圆形 circle = {x, y, r}; // 圆心与半径
首先是 x 轴:
如果圆心在矩形的左侧(if(circle.x < rect.x)),那么 closestPoint.x = rect.x。
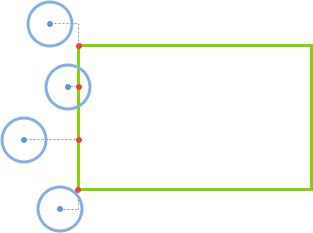
如果圆心在矩形的右侧(else if(circle.x > rect.x + rect.w)),那么 closestPoint.x = rect.x + rect.w。
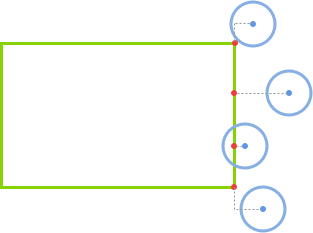
如果圆心在矩形的正上下方(else),那么 closestPoint.x = circle.x。
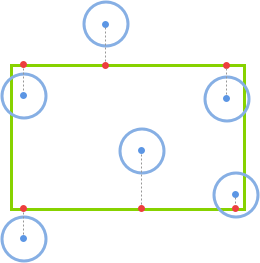
同理,对于 y 轴(此处不列举图例):
如果圆心在矩形的上方(if(circle.y < rect.y)),那么 closestPoint.y = rect.y。
如果圆心在矩形的下方(else if(circle.y < rect.y + rect.h)),那么 closestPoint.y = rect.y + rect.h。
圆形圆心在矩形的正左右两侧(else),那么 closestPoint.y = circle.y。
因此,通过上述方法即可找出矩形上离圆心最近的点了,然后通过『两点之间的距离公式』得出『最近点』与『圆心』的距离,最后将其与圆的半径相比,即可判断是否发生碰撞。
var distance = Math.sqrt(Math.pow(closestPoint.x - circle.x, 2) + Math.pow(closestPoint.y - circle.y, 2))
if(distance < circle.r) return true // 发生碰撞
else return false // 未发生碰撞
在线运行示例:
在线运行示例:See the Pen Circle and Rectangle
圆形与旋转矩形(以矩形中心为旋转轴)
概念:即使矩形以其中心为旋转轴进行了旋转,但是判断它与圆形是否发生碰撞的本质还是找出矩形上离圆心的最近点。
对于旋转后的矩形,要找出其离圆心最近的点,似乎有些困难。其实,我们可以将我们思想的范围进行扩大:将矩形的旋转看作是整个画布的旋转。那么我们将画布(即 Canvas)反向旋转『矩形旋转的角度』后,所看到的结果就是上一个方法“圆形与矩形(无旋转)”的情形。因此,我们只需求出画布旋转后的圆心位置,即可使用『圆形与矩形(无旋转)』的判断方法了。
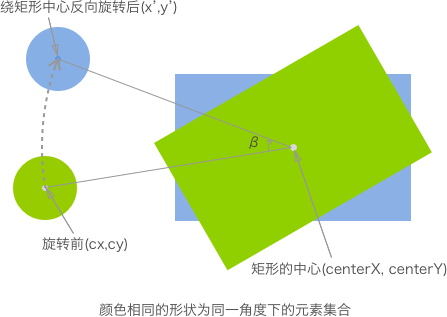
先给出可直接套用的公式,从而得出旋转后的圆心坐标:
x’ = cos(β) * (cx – centerX) – sin(β) * (cy – centerY) + centerX
y’ = sin(β) * (cx – centerX) + cos(β) * (cy – centerY) + centerY
该公式的推导过程:
根据下图,计算某个点绕另外一个点旋转一定角度后的坐标。我们设 A(x,y) 绕 B(a,b) 旋转 β 度后的位置为 C(c,d)。
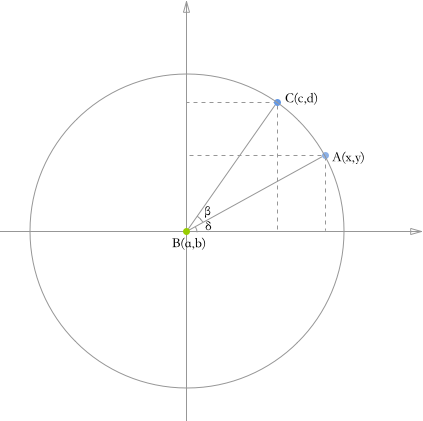
- 设 A 点旋转前的角度为 δ,则旋转(逆时针)到 C 点后的角度为(δ+β)
- 由于 |AB| 与 |CB| 相等(即长度),且
- |AB| = y/sin(δ) = x / cos(δ)
- |CB| = d/sin(δ + β) = c / cos(δ + β)
- 半径 r = x / cos(δ) = y / sin(δ) = d / sin(δ + β) = c / cos(δ + β)
- 由以下三角函数两角和差公式:
- sin(δ + β) = sin(δ)cos(β) + cos(δ)sin(β)
- cos(δ + β) = cos(δ)cos(β) - sin(δ)sin(β)
- 可得出旋转后的坐标:
- c = r * cos(δ + β) = r * cos(δ)cos(β) - r * sin(δ)sin(β) = x * cos(β) - y * sin(β)
- d = r * sin(δ + β) = r * sin(δ)cos(β) + r * cos(δ)sin(β) = y * cos(β) + x * sin(β)
由上述公式推导后可得:旋转后的坐标 (c,d) 只与旋转前的坐标 (x,y) 及旋转的角度 β 有关。
注意:(c,d) 是旋转一定角度后(相对于旋转点的坐标)。因此,前面提到的(可直接套用的公式)中加上了矩形的中心点(旋转中心点)的坐标值。
从图中也可以得出以下结论:A 点旋转后的 C 点总是在圆周(半径为 |AB|)上运动,利用这点可让物体绕旋转点(轴)做圆周运动。
得到旋转后的圆心坐标值后,即可使用(圆形与矩形(无旋转))方法进行碰撞检测了。
在线运行示例:https://codepen.io/JChehe/pen/dWmYjO
总结:
优点:投影与横纵坐标轴上,计算简单
缺点:未考虑车辆姿态的矩形框图,会降低可行域
需要感知的信息:物体AABB下左上角点位置及框图的尺寸(长和宽)
OBB-box
OBB-box会跟着物体的朝向一起旋转,而大小不会改变,相对来说比AABB-box更加准确,但是检测碰撞的运算量会比AABB-box大一点。
优点:OBB考虑到车辆的姿态,框图面积更小,可行域的损失较小
缺点:投影方式相较于AABB复杂,计算量较大
地图格子划分
概念:将地图(场景)划分为一个个格子。地图中参与检测的对象都存储着自身所在格子的坐标,那么你即可以认为两个物体在相邻格子时为碰撞,又或者两个物体在同一格才为碰撞。另外,采用此方式的前提是:地图中所有可能参与碰撞的物体都要是格子单元的大小或者是其整数倍。
蓝色X 为障碍物:

// 通过特定标识指定(非)可行区域
map = [
[0, 0, 1, 1, 1, 0, 0, 0, 0],
[0, 1, 1, 0, 0, 1, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 1, 0, 0],
[0, 1, 0, 0, 0, 0, 1, 0, 0],
[0, 1, 1, 1, 1, 1, 1, 0, 0]
],
// 设定角色的初始位置
player = {left: 2, top: 2}
// 移动前(后)判断角色的下一步的动作(如不能前行)
...
在线运行示例:
在线运行示例: [See the Pen map cell collision detection( http://codepen.io/JChehe/pen/pRqqGV/ )
缺点:
- 适用场景局限。
适用案例:
- 推箱子、踩地雷等
像素检测
概念:以像素级别检测物体之间是否存在重叠,从而判断是否碰撞。
实现方法有多种,下面列举在 Canvas 中的两种实现方式:
- 如下述的案例中,通过将两个物体在 offscreen canvas 中判断同一位置(坐标)下是否同时存在非透明的像素。
- 利用 canvas 的
globalCompositeOperation = 'destination-in'属性。该属性会让两者的重叠部分会被保留,其余区域都变成透明。因此,若存在非透明像素,则为碰撞。
注意,当待检测碰撞物体为两个时,第一种方法需要两个 offscreen canvas,而第二种只需一个。
offscreen canvas:与之相关的是 offscreen rendering。正如其名,它会在某个地方进行渲染,但不是屏幕。“某个地方”其实是内存。渲染到内存比渲染到屏幕更快。—— Offscreen Rendering
当然,我们这里并不是利用 offscreen render 的性能优势,而是利用 offscreen canvas 保存独立物体的像素。换句话说:onscreen canvas 只是起展示作用,碰撞检测是在 offscreen canvas 中进行。
另外,由于需要逐像素检测,若对整个 Canvas 内所有像素都进行此操作,无疑会浪费很多资源。因此,我们可以先通过运算得到两者相交区域,然后只对该区域内的像素进行检测即可。
图例:
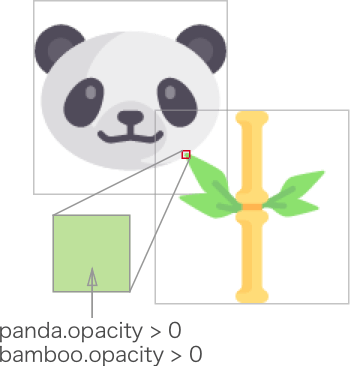
在线运行示例:
http://codepen.io/JChehe/pen/qRLLzB/
缺点:
- 因为需要检查每一像素来判定是否碰撞,性能要求比较高。
适用案例:
- 需要以像素级别检测物体是否碰撞。
精细碰撞检测
SAT(Separating Axis Theorem分离轴定理)
概念:通过判断任意两个 凸多边形 在任意角度下的投影是否均存在重叠,来判断是否发生碰撞。若在某一角度光源下,两物体的投影存在间隙,则为不碰撞,否则为发生碰撞。
图例:
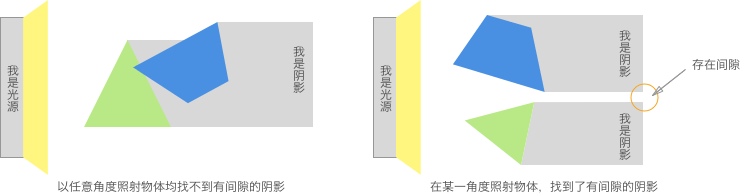
在程序中,遍历所有角度是不现实的。那如何确定 投影轴 呢?其实投影轴的数量与多边形的边数相等即可。

以较高抽象层次判断两个凸多边形是否碰撞:
function polygonsCollide(polygon1, polygon2) {
var axes, projection1, projection2
// 根据多边形获取所有投影轴
axes = polygon1.getAxes()
axes.push(polygon2.getAxes())
// 遍历所有投影轴,获取多边形在每条投影轴上的投影
for(each axis in axes) {
projection1 = polygon1.project(axis)
projection2 = polygon2.project(axis)
// 判断投影轴上的投影是否存在重叠,若检测到存在间隙则立刻退出判断,消除不必要的运算。
if(!projection1.overlaps(projection2))
return false
}
return true
}
三个问题:
上述代码有几个需要解决的地方:
- 问题一:如何确定多边形的各个投影轴
- 问题二:如何将多边形投射到某条投影轴上
- 问题三:如何检测两段投影是否发生重叠
投影轴
如下图所示,我们使用一条从 p1 指向 p2 的向量来表示多边形的某条边,我们称之为边缘向量。在分离轴定理中,还需要确定一条垂直于边缘向量的法向量,我们称之为“边缘法向量”。
投影轴平行于边缘法向量。投影轴的位置不限,因为其长度是无限的,故而多边形在该轴上的投影是一样的。该轴的方向才是关键的。
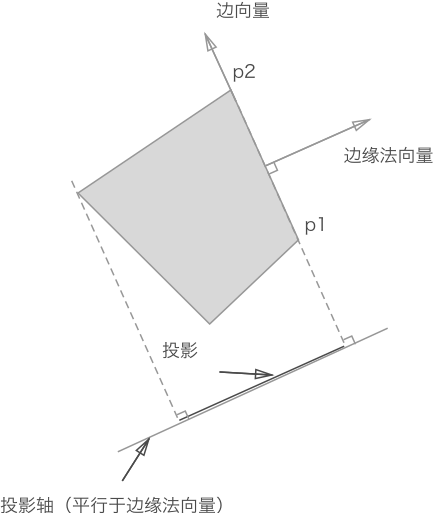
// 以原点(0,0)为始,顶点为末。最后通过向量减法得到 边缘向量。
var v1 = new Vector(p1.x, p1.y)
v2 = new Vector(p2.x, p2.y)
// 首先得到边缘向量,然后再通过边缘向量获得相应边缘法向量(单位向量)。
// 两向量相减得到边缘向量 p2p1(注:上面应该有个右箭头,以表示向量)。
// 设向量 p2p1 为(A,B),那么其法向量通过 x1x2+y1y2 = 0 可得:(-B,A) 或 (B,-A)。
axis = v1.edge(v2).normal()
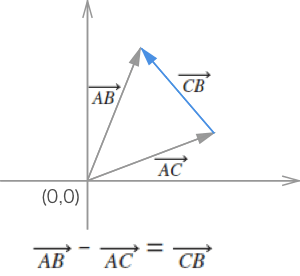
向量相减
更多关于向量的知识可通过其它渠道学习。
投影
投影的大小:通过将一个多边形上的每个顶点与原点(0,0)组成的向量,投影在某一投影轴上,然后保留该多边形在该投影轴上所有投影中的最大值和最小值,这样即可表示一个多边形在某投影轴上的投影了。
判断两多边形的投影是否重合:projection1.max > projection2.min && project2.max > projection.min
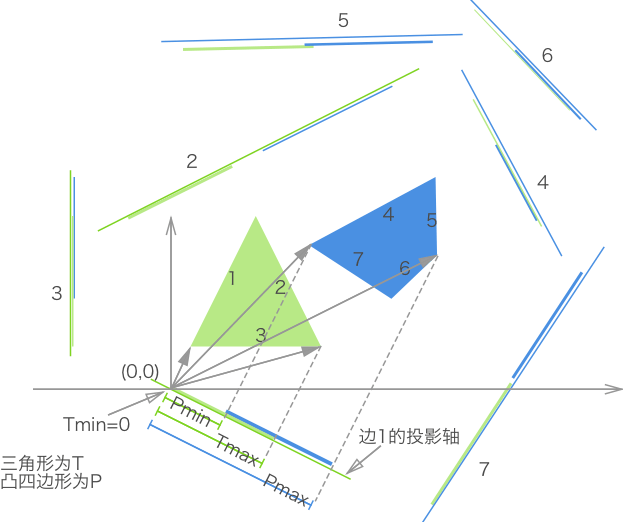
为了易于理解,示例图将坐标轴原点(0,0)放置于三角形边1投影轴的适当位置。
由上述可得投影对象:
// 用最大和最小值表示某一凸多边形在某一投影轴上的投影位置
var Projection = function (min, max) {
this.min
this.max
}
projection.prototype = {
// 判断两投影是否重叠
overlaps: function(projection) {
return this.max > projection.min && projection.max > this.min
}
}
如何得到向量在投影轴上的长度?
向量的点积的其中一个几何含义是:一个向量在平行于另一个向量方向上的投影的数值乘积。
由于投影轴是单位向量(长度为1),投影的长度为 x1 * x2 + y1 * y2
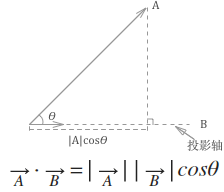
// 根据多边形的每个定点,得到投影的最大和最小值,以表示投影。
function project = function (axis) {
var scalars = [], v = new Vector()
this.points.forEach(function (point) {
v.x = point.x
v.y = point.y
scalars.push(v.dotProduct(axis))
})
return new Projection(Math.min.apply(Math, scalars),
Math.max,apply(Math, scalars))
}
圆形与多边形之间的碰撞检测
由于圆形可近似地看成一个有无数条边的正多边形,而我们不可能按照这些边一一进行投影与测试。我们只需将圆形投射到一条投影轴上即可,这条轴就是圆心与多边形顶点中最近的一点的连线,如图所示:
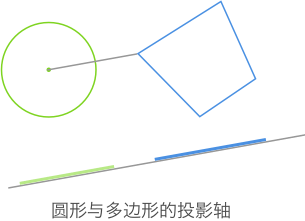
因此,该投影轴和多边形自身的投影轴就组成了一组待检测的投影轴了。
而对于圆形与圆形之间的碰撞检测依然是最初的两圆心距离是否小于两半径之和。
分离轴定理的整体代码实现,可查看以下案例:
实现案例:
http://codepen.io/JChehe/pen/KabEaw/
优点:
- 精确
缺点:
- 不适用于凹多边形
适用案例:
- 任意凸多边形和圆形。
更多关于分离轴定理的资料:
- Separating Axis Theorem (SAT) explanation
- Collision detection and response
- Collision detection Using the Separating Axis Theorem
- SAT (Separating Axis Theorem)
- Separation of Axis Theorem (SAT) for Collision Detection
- “等一下,我碰!”——常见的2D碰撞检测
GJK(Gilbert–Johnson–Keerthi)算法
在精细碰撞检测中,除了 SAT ,另外一个就是 GJK方法。做了一定的加速处理,它也只适用于凸多边形间的碰撞检测。
主要思想:当两个图形发生重叠时,那么在两个图形中一定存在一对点,相减后为原点
EPA (Expanding Polytope Algorithm)
https://zhuanlan.zhihu.com/p/178841676


