路径规划中曲率问题

1、什么是曲率

百科解释：曲线的曲率（curvature）就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。
曲率越大表示曲线的弯曲程度越大。曲率的倒数就是曲率半径。

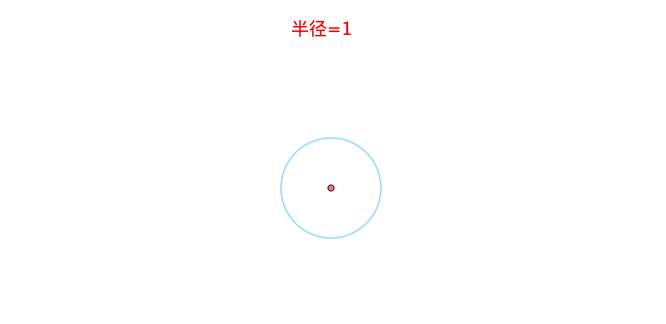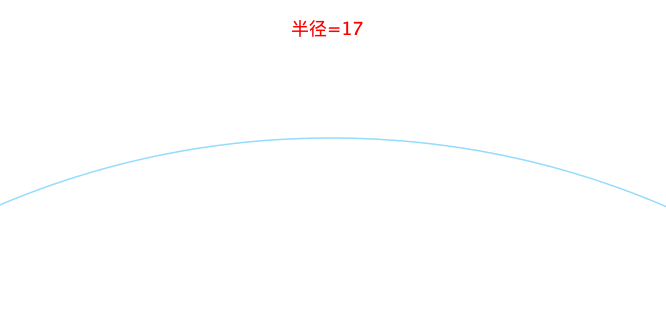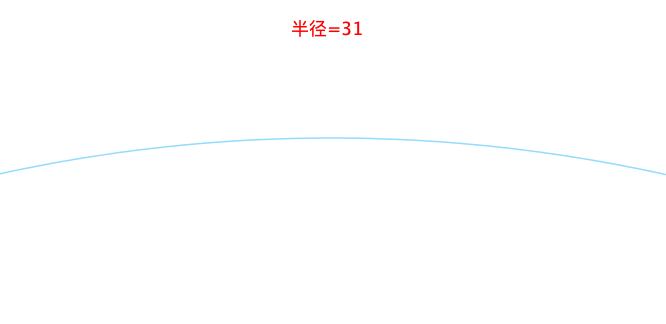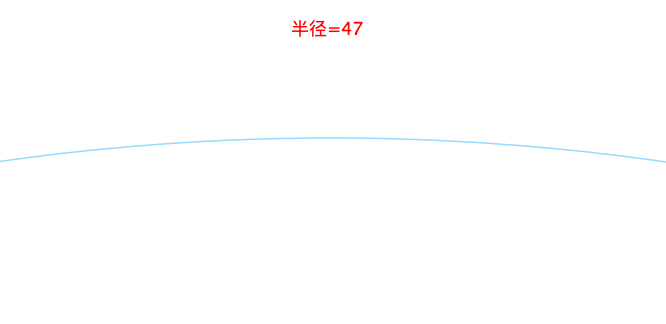
2、曲率计算方式

2.1 连续曲线下的曲率计算

2.1.1 直角坐标方程下计算曲率

设曲线的直角坐标方程为y=f（x），且y=f（x）具有二阶导数，曲线在点M处的切线的斜率为

 ,所以

又

 ,故曲线L在M点处的曲率为

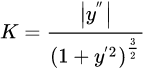
2.1.2 参数方程下计算曲率

设曲线是由参数方程

 给出，利用参数方程求导法可得

2.2 离散点下曲率计算(路径规划中常用)

三点确定曲率

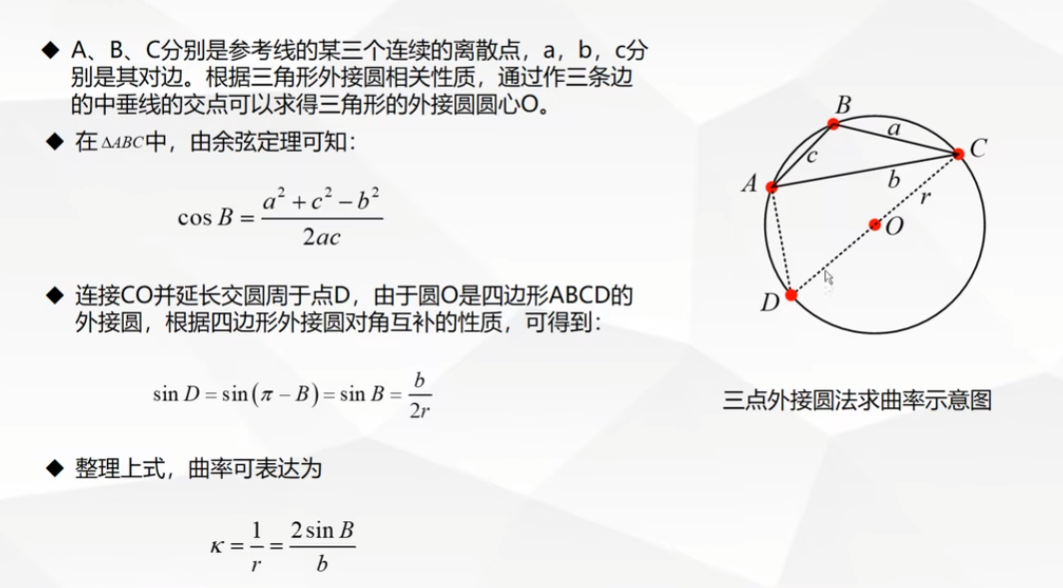
// An highlighted block
try
{   //取点 P1、P2、P3是位置信息
    A = PT1.pose.position;
    B = PT2.pose.position;
    C = PT3.pose.position;
    double curvity;
    //计算曲率部分，使用正弦定理 a/sinA = 2R
    if(A.x == B.x == C.x)//三点横坐标相同，即共线，直接标记曲率为0
    {
        curvity = 0;
    }
    else
    {
        double a,b,c; r;
        double cosA,sinA,dis;
        c = sqrt((A.x - B.x)*(A.x - B.x) + (A.y - B.y)*(A.y - B.y));
        b = sqrt((A.x - C.x)*(A.x - C.x) + (A.y - C.y)*(A.y - C.y));
        a = sqrt((B.x - C.x)*(B.x - C.x) + (B.y - C.y)*(B.y - C.y));
        dis = a*a + c*c - b*b;
        cosB = dis/(2*dis1*dis3);//余弦定理求角度
        sinB = sqrt(1 - cosA*cosA);//求正弦
        r = 0.5*b/sinB;//正弦定理求外接圆半径
        curvity = 1/r;//半径的倒数是曲率，半径越小曲率越大
    }
    cout<<"curvity = "<<curvity<<"\n";
}
catch(tf::TransformException &ex)//处理意外情况
{
    ROS_ERROR("%s",ex.what());
    cout<<"三点取点失败\n";
}

离散点计算曲率（介绍了采用多个点，使用最小二乘法进行曲率运算）

2.3 车辆运动过程中曲率计算

3、曲率在路径规划中的一些问题

3.1曲率不连续点是什么：

是即使两个相邻段之间是平滑连接的，但是两个段具有不同或不同方向的曲率。大多数这样的光滑连接，其实际上是间断点（曲率不连续点）。在该类型的不连续点上，所有相关坐标轴都表现出加速度的不连续性。

参考文章：

3.2 避免猛打方向盘

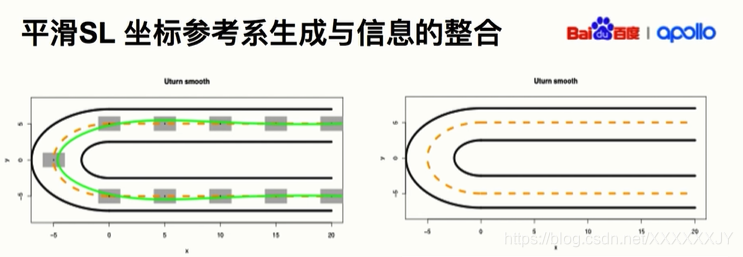
若生成右图所示的路径，那么乘坐感会较差，因为在直线与转弯的交界处需要猛打方向盘。所以先根据道路中心线获得左图的若干小黑点，然后生成灰色的框，希望规划的路径尽可能平稳地穿过这个灰色的框，并且满足曲率2阶可导（这样就避免猛打方向盘了）。

如何通俗地理解曲率？
估计自车轨迹曲率的方法
ACS运动控制：轨迹拐点、曲率不连续点
三点法求曲率，使用C++实现