汽车二自由度模型公式推导及simulink模型——传递函数、状态空间
二自由度车辆方程
1、简化与假设
为便于掌握操纵稳定性的基本特性,我们将一对简化为线性二自由度的汽车模型进行研究,分析中忽略一下几点:
1、忽略转向系统的影响,直接以前轮转角作为输入。
2、忽略悬架的作用,认为汽车车厢只作平行于地面的平面运动,即汽车沿z轴的位移,绕y轴的俯仰角与绕x轴的侧倾角均为零。
3、另外,汽车沿着x轴的前进速度u视为不变。因为之后将用运动学和动力学的方式联立等式(理论力学的内容),而沿x轴速度不变意味着x轴方向的加速度为0,不用参与到联立的等式中。
因此,汽车只有沿y轴的侧向运动与绕z轴的横摆运动这样两个自由度。
此外,汽车的侧向加速度限定在0.4g以下,轮胎侧偏特性处于线性范围。在建立运动微分方程时还假设:驱动力不大,不考虑地面切向力对轮胎侧偏特性的影响,没有空气动力的作用,忽略左、右车车轮轮胎由于载荷的变化而引起轮胎特性的变化以及轮胎回正力矩的作用。这样,实际汽车便简化成为一个两轮摩托车模型。
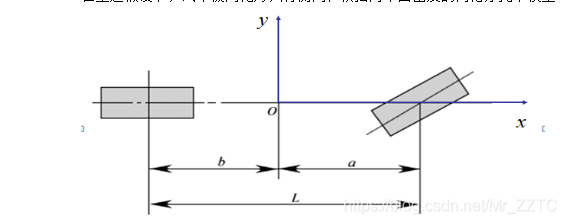
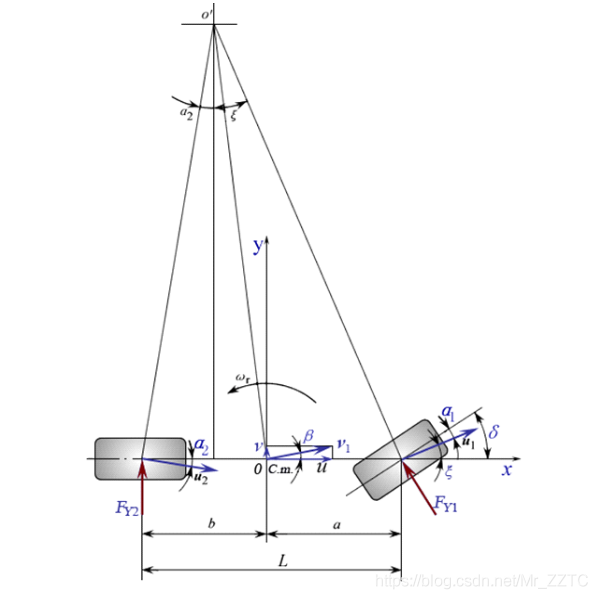
Fig2. 二自由度汽车模型
2、汽车运动分析
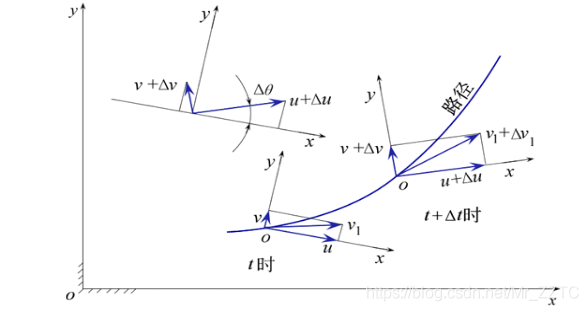
Fig .3 l利用固结与汽车的车辆坐标系分析汽车的运动
很小,且忽略二阶微量
车辆沿ox轴和oy轴的速度分量
求取汽车质心得绝对加速度在车辆坐标系ox轴和oy轴的速度分量
二自由度汽车受到的外力沿y轴方向的合力与绕质心的力矩和力:
考虑前轮转角很小,上式可以写成:
引入质心侧偏角:
是u1和x轴的夹角:
前后轮转角偏差:
综上所述,可以列出外力、外力矩与汽车运动参数的关系式:
整理后得到二自由度运动微分方程:
线性二自由度汽车模型的运动微分方程包含了最重要的汽车质量和轮胎侧偏刚度两方面的参数,所以能够反映汽车曲线运动最基本的特征。
可以看出,汽车的横摆、侧向运动与前后轮的侧偏刚度、纵向车速、质心位置、前轮转角、整车质量有关。其中,纵向车速、前轮转角是驾驶员控制的,所谓转弯时减速慢行就是防止由于侧向加速度过大导致侧滑、侧偏甚至侧翻。整车质量、质心位置、前后轮侧偏刚度是车辆的固有特性,就是工程师应该在设计时应该考虑的,保证车辆有较好的转向特性,一般可以通过稳定性因子K来确定车辆稳定性。
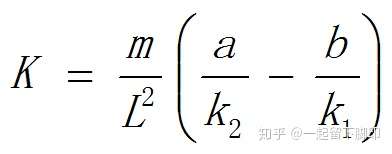
K大于0时,具有不足转向特性,横摆角速度可控;
K小于0时,具有过度转向特性,超过一定车速车辆将失稳。
将上面的微分方程可以继续整理成状态空间形式:
上述是非常重要的两个公式,衡量了瞬态汽车运动时的侧向加速度和横摆角速度。为简化表达式。我们设如下参数:

上述方程可以通过传递函数和状态空间表示。这两种方法皆能用来设计闭环控制系统,通过将所测得的汽车性能参数调整至理想数值来提升车辆稳定性,也及ESC系统作用。
传递函数法
上述等式可写为:


联立可得:



(过程推导)


角速度稳态增益和速度增益如下:






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 25岁的心里话
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· 零经验选手,Compose 一天开发一款小游戏!
· 通过 API 将Deepseek响应流式内容输出到前端
· AI Agent开发,如何调用三方的API Function,是通过提示词来发起调用的吗
2021-05-02 无人驾驶—预测系统
2021-05-02 03. Pandas数据结构
2021-05-02 python中dtype,type,astype的区别
2021-05-02 pandas数据读取
2021-05-02 什么是pandas
2021-05-02 Numpy实现多项式曲线拟合
2021-05-02 Numpy实现SVD矩阵分解