8基于模型预测控制的路径规划
Introduction
- Model
- System model(质点本身的运动)
- Problem model(一般需要非线性方法来解决)
- Prediction
- State space
- Input space
- Parameter space
- Control
- The process of choosing the best policy
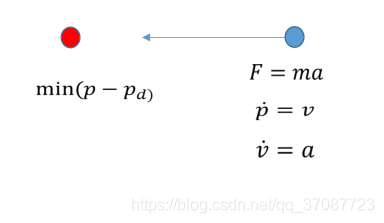
Model
模型预测控制通常的描述
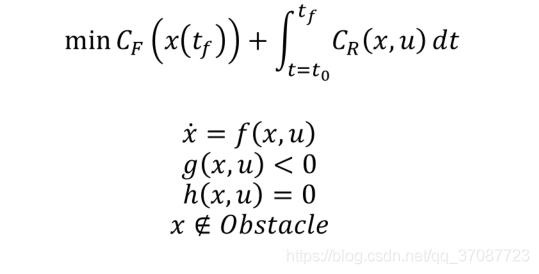
final cost,tf关于系统最后的状态的函数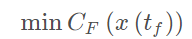
running cost,t0-tf之间的cost,关于系统状态的函数
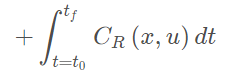
约束分别为:
动力学约束(微分约束)
不等式约束(关于功率,加速度和速度等限制)
等式约束(从系统的一个状态到另一个状态的边界约束)
障碍物约束(特殊,通常非凸的)
Parameter space
在预测轨迹有作用.
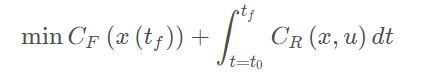
目的:找寻最佳的输入u uu
需要将无限维度的输入转化到有限维度的输入.
方法:
- 零阶保持器(直接采样离散化),如下图有13段调整的输入
- 多项式(将输入转化为多项式,调整a,b,c,d参数)
- B样条
- 数值解方法
- 有限Jerk轨迹
- 基于神经网络的方法

Optimization
- 搜索:
- 图搜索
- 基于随机抽样的搜索
- 凸优化:
- 二次规划,解决线性优化
- 非凸优化:
- 序列二次规划
- 粒子群优化解决非线性,不连续的优化
Control
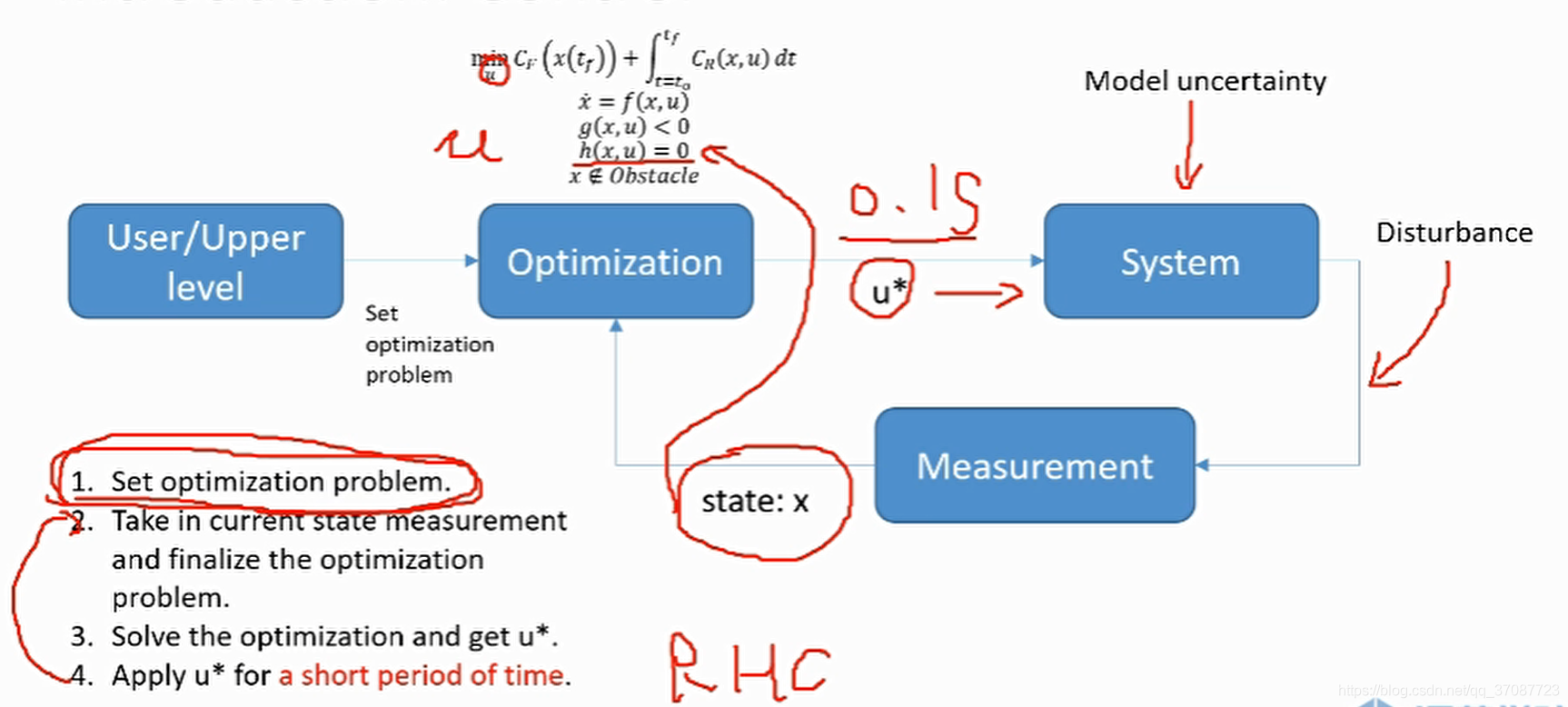
优化的输入u ∗ ,只在0.1s内(假定)去求解,不断重新解的u,这个过程被称为RHC(Receding Horizon Control)
Tube based MPC
为了解决需要快速响应的系统问题,控制频率要求高
多了Nominal system ,也就是标称名义系统模型,不考虑外界干扰,能以较低的频率解优化问题,较高的频率控制.应用广泛。
之所以叫Tube based MPC,是因为Associate controller可以使我们的real state 镇定在reference trajectory附近,形成一个管道。
[论文](Tube-Based MPC: a Contraction Theory Approach)
Convenient sources
• Matlab MPC toolbox:
内置教学,可以作为代码生成.
• μAO-MPC:
可以作为代码生成.
• Acado toolkit:
可以作为代码生成.解决非线性问题
• YANE:
大量的非线性算子
• Multi-Parametric Toolbox 3:
显示MPC,不同于前面的使用数值优化,查表法,较高效
Linear Model Predictive Control
4s为prediction horizon
4s分成20段

变为矩阵描述
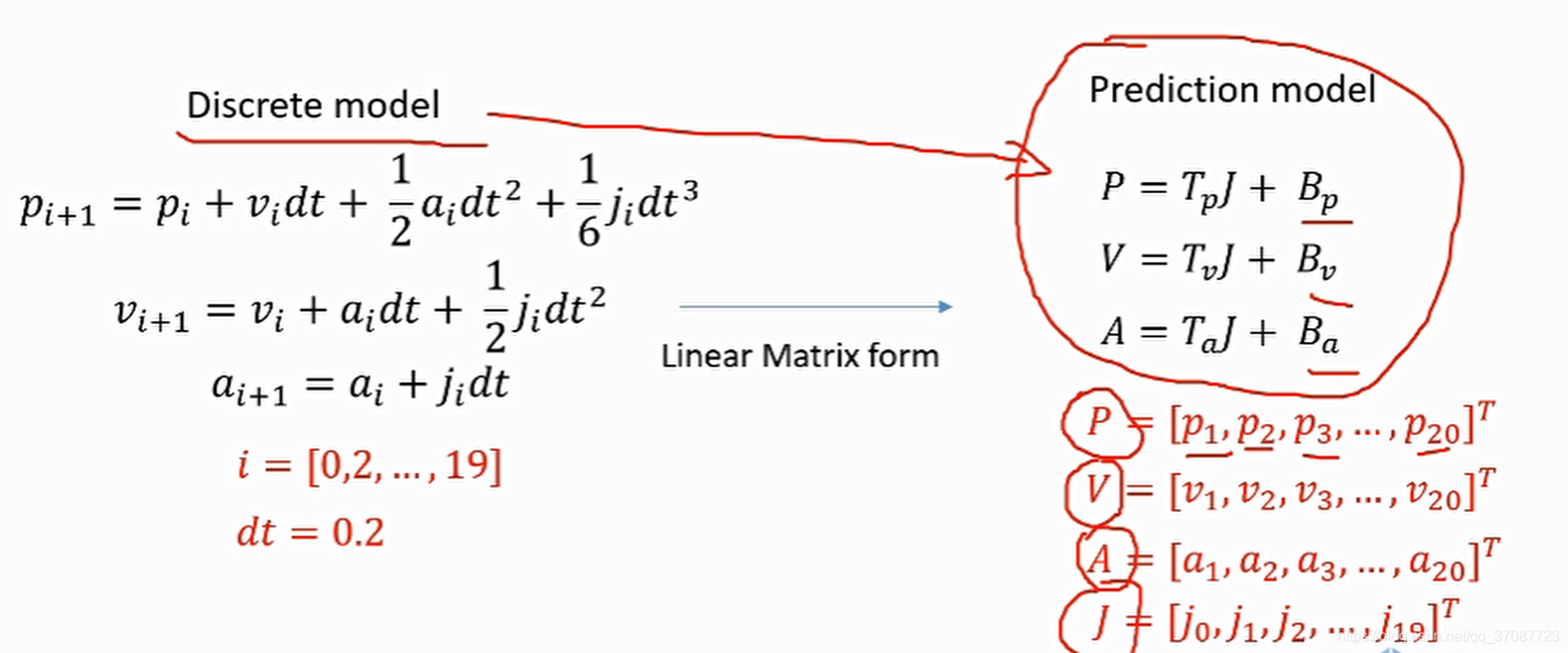
预测模型
解Tp , Tv , Ta参考如下代码,大致思路就是便是将这几个量(p,v,a)化为关于j的表达式
function [Tp, Tv, Ta, Bp, Bv, Ba] = getPredictionMatrix(K,dt,p_0,v_0,a_0)
Ta=zeros(K);
Tv=zeros(K);
Tp=zeros(K);
for i = 1:K
Ta(i,1:i) = ones(1,i)*dt;
end
for i = 1:K% K为i
for j = 1:i
Tv(i,j) = (i-j+0.5)*dt^2;%
end
end
for i = 1:K
for j = 1:i
Tp(i,j) = ((i-j+1)*(i-j)/2+1/6)*dt^3;
end
end
Ba = ones(K,1)*a_0;
Bv = ones(K,1)*v_0;
Bp = ones(K,1)*p_0;
for i=1:K
Bv(i) = Bv(i) + i*dt*a_0;
Bp(i) = Bp(i) + i*dt*v_0 + i^2/2*a_0*dt^2;
end
问题模型:
假设
**目标1:**最终要到达零位置,零速度,零加速度。优化函数

**目标2:**平滑轨迹。优化函数![]()
wn为权重
整体优化目标:
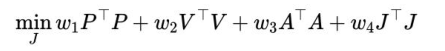
其中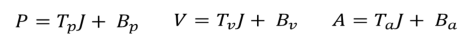
通过上两式的变化有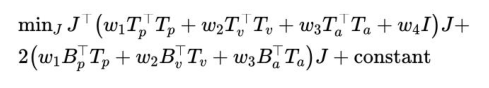
这是一个凸优化问题,使用MATLAB 的quadprog()求解二次规划问题
clear all;
close all;
clc;
p_0 = 10;
v_0 = 0;
a_0 = 0;
K=20;
dt=0.2;
log=[0 p_0 v_0 a_0];
w1 = 100;
w2 = 1;
w3 = 1;
w4 = 1;
for t=0.2:0.2:10
%% Construct the prediction matrix
[Tp, Tv, Ta, Bp, Bv, Ba] = getPredictionMatrix(K,dt,p_0,v_0,a_0);
%% Construct the optimization problem
H = w4*eye(K)+w1*(Tp'*Tp)+w2*(Tv'*Tv)+w3*(Ta'*Ta);
F = w1*Bp'*Tp+w2*Bv'*Tv+w3*Ba'*Ta;
%% Solve the optimization problem
J = quadprog(H,F,[],[]);
%% Apply the control
j = J(1);
p_0 = p_0 + v_0*dt + 0.5*a_0*dt^2 + 1/6*j*dt^3;
v_0 = v_0 + a_0*dt + 0.5*j*dt^2;
a_0 = a_0 + j*dt;
%% Log the states
log = [log; t p_0 v_0 a_0];
end
%% Plot the result
plot(log(:,1),log(:,2:4));
grid on;
xlabel('t(s)');
legend('p','v','a');
其中:
K = 20, 表示20个时间段,每段0.2s,共计预测未来4s内输出
log记录系统轨迹
调节四个权重的值
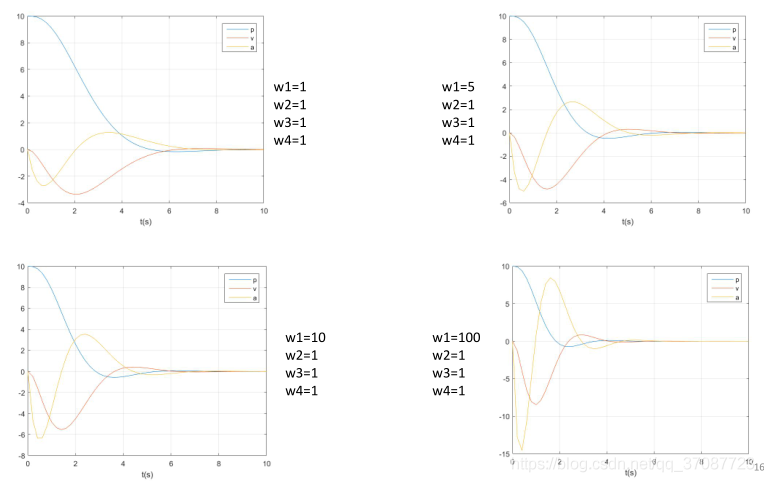
J 的解析解,不去解QP问题,可能效率会更高些J=-inv(H)*F';%J的解析解

hard constraints

由于许多求解器使用的都是小于形式,所以需要化为四组约束条件,写成代码A J < b
clear all;
close all;
clc;
p_0 = 10;
v_0 = 0;
a_0 = 0;
K=20;
dt=0.2;
log=[0 p_0 v_0 a_0];
w1 = 100;
w2 = 1;
w3 = 1;
w4 = 1;
for t=0.2:0.2:20
%% Construct the prediction matrix
[Tp, Tv, Ta, Bp, Bv, Ba] = getPredictionMatrix(K,dt,p_0,v_0,a_0);
%% Construct the optimization problem
H = w4*eye(K)+w1*(Tp'*Tp)+w2*(Tv'*Tv)+w3*(Ta'*Ta);
F = w1*Bp'*Tp+w2*Bv'*Tv+w3*Ba'*Ta;
A = [Tv;-Tv;Ta;-Ta];
b = [ones(20,1)-Bv;ones(20,1)+Bv;ones(20,1)-Ba;ones(20,1)+Ba];%[-1,1]
%% Solve the optimization problem
J = quadprog(H,F,A,b);
%% Apply the control
j = J(1);
p_0 = p_0 + v_0*dt + 0.5*a_0*dt^2 + 1/6*j*dt^3;
v_0 = v_0 + a_0*dt + 0.5*j*dt^2;
a_0 = a_0 + j*dt;
%% Log the states
log = [log; t p_0 v_0 a_0];
end
%% Plot the result
plot(log(:,1),log(:,2:4));
grid on;
xlabel('t(s)');
legend('p','v','a');
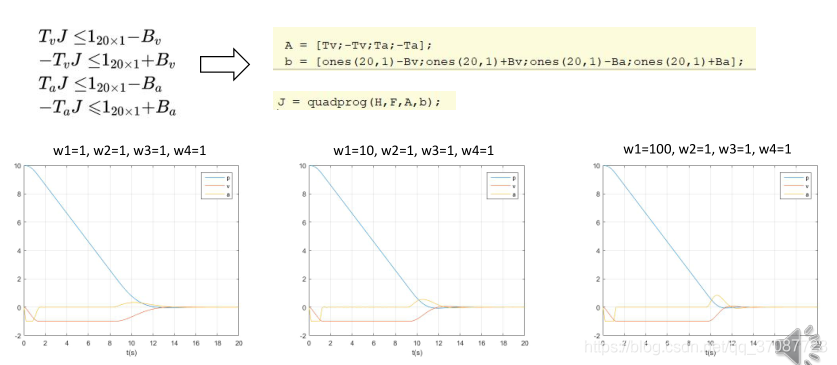
预测时域只有4s,所以无法在如此短的时间内位置从10m达到0m,这是由于限制了速度和加速度1 m / s 1m/s1m/s,无法求得解.
所以将目标放到优化函数,这样至少有一个解.
note:模型预测控制受限于预测时域,但如果要扩大模型预测时域,会使得系统的计算负担加大,而太短则会使得系统无法镇定,从而发散.
soft constraints
如果速度和加速度不可避免超出约束限制呢 ?比如刮风
如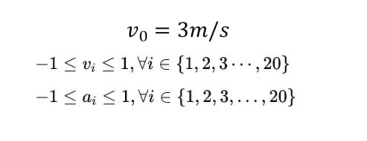
那么求解器会没有解,控制器也不知道该如何去控制?
此时需要将惩罚函数(S ( V ) )添加到优化目标,不过这样不能使用二次规划问题.
一般使用指数函数,但这样在转角位置不可导,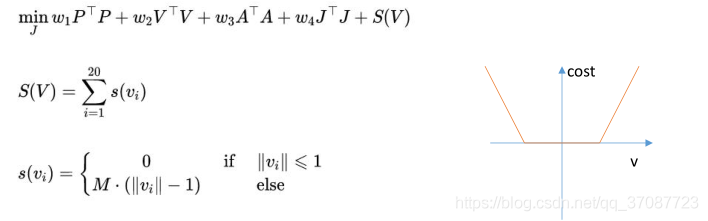

M是一个很大的正数
L要足够大,使得等式成立,又不能太大,不然会超过约束条件太多,所以加入 w s ∗ L T ∗ L 这样能够用二次优化问题来求解.
clear all;
close all;
clc;
p_0 = 10;
v_0 = -3;
a_0 = 0;
K=20;
dt=0.2;
log=[0 p_0 v_0 a_0];
w1 = 10;
w2 = 1;
w3 = 1;
w4 = 1;
w5 = 1e4;
for t=0.2:0.2:20
%% Construct the prediction matrix
[Tp, Tv, Ta, Bp, Bv, Ba] = getPredictionMatrix(K,dt,p_0,v_0,a_0);
%% Construct the optimization problem
H = blkdiag(w4*eye(K)+w1*(Tp'*Tp)+w2*(Tv'*Tv)+w3*(Ta'*Ta),w5*eye(K));%note w5->M
F = [w1*Bp'*Tp+w2*Bv'*Tv+w3*Ba'*Ta zeros(1,K)];
A = [Tv zeros(K);-Tv -eye(K);Ta zeros(K); -Ta zeros(K); zeros(size(Ta)) -eye(K)];%-eye(K)->L
b = [ones(20,1)-Bv;ones(20,1)+Bv;ones(20,1)-Ba;ones(20,1)+Ba; zeros(K,1)];
%% Solve the optimization problem
J = quadprog(H,F,A,b);
%% Apply the control
j = J(1);
p_0 = p_0 + v_0*dt + 0.5*a_0*dt^2 + 1/6*j*dt^3;
v_0 = v_0 + a_0*dt + 0.5*j*dt^2;
a_0 = a_0 + j*dt;
%% Log the states
log = [log; t p_0 v_0 a_0];
end
%% Plot the result
plot(log(:,1),log(:,2:4));
grid on;
xlabel('t(s)');
legend('p','v','a');
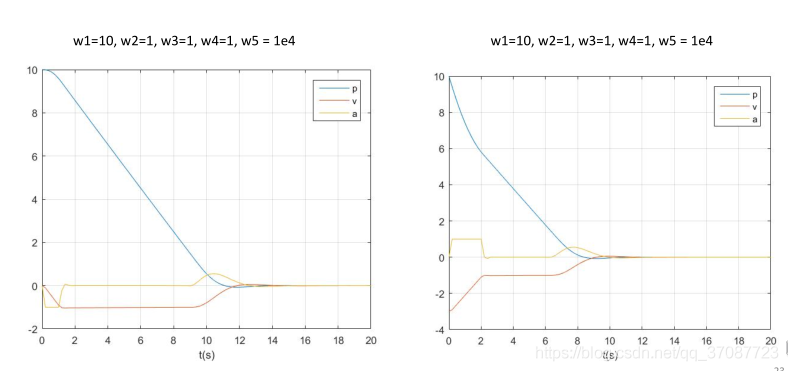
Design rule
设计状态时考虑软约束,以免没有解
- 它们受到测量噪声和干扰的影响
输入考虑硬约束 - 它们可以任意变化,不受噪音干扰,超过约束可能会损害物理系统
limitation
- 通常需要线性模型,或者模型可以合理的线性化(自适应MPC) ,参考MATLAB
- 障碍约束通常具有非凸性。如下图所示,障碍物为蓝色,在外面为或的关系,是非凸的.
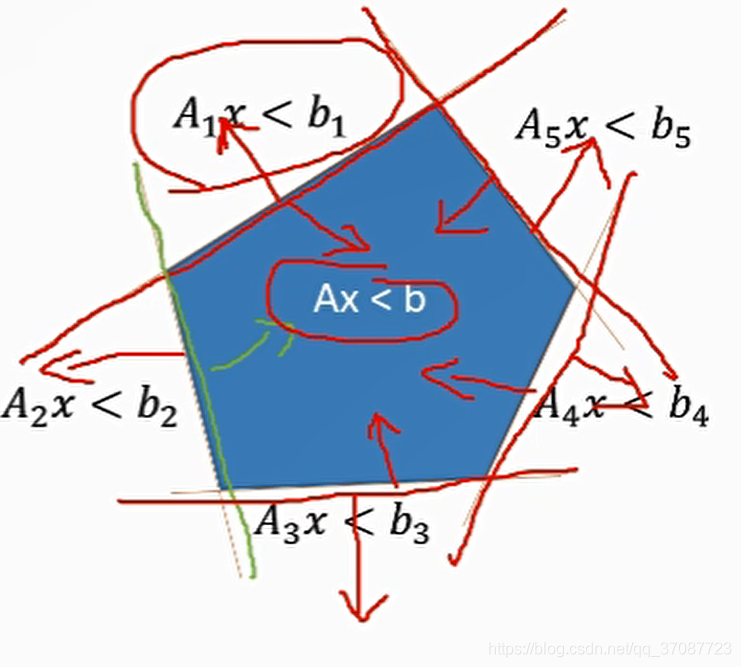
Parameter space: Boundary constrained motion primitives (BSCP)
-
多项式参数空间

- 零阶保持参数空间

- BSCP

Parameter space: Jerk limited trajectory
我们不仅需要有限的冲击jerk,而且还有有限的加速度和速度。
将称其为JLT。
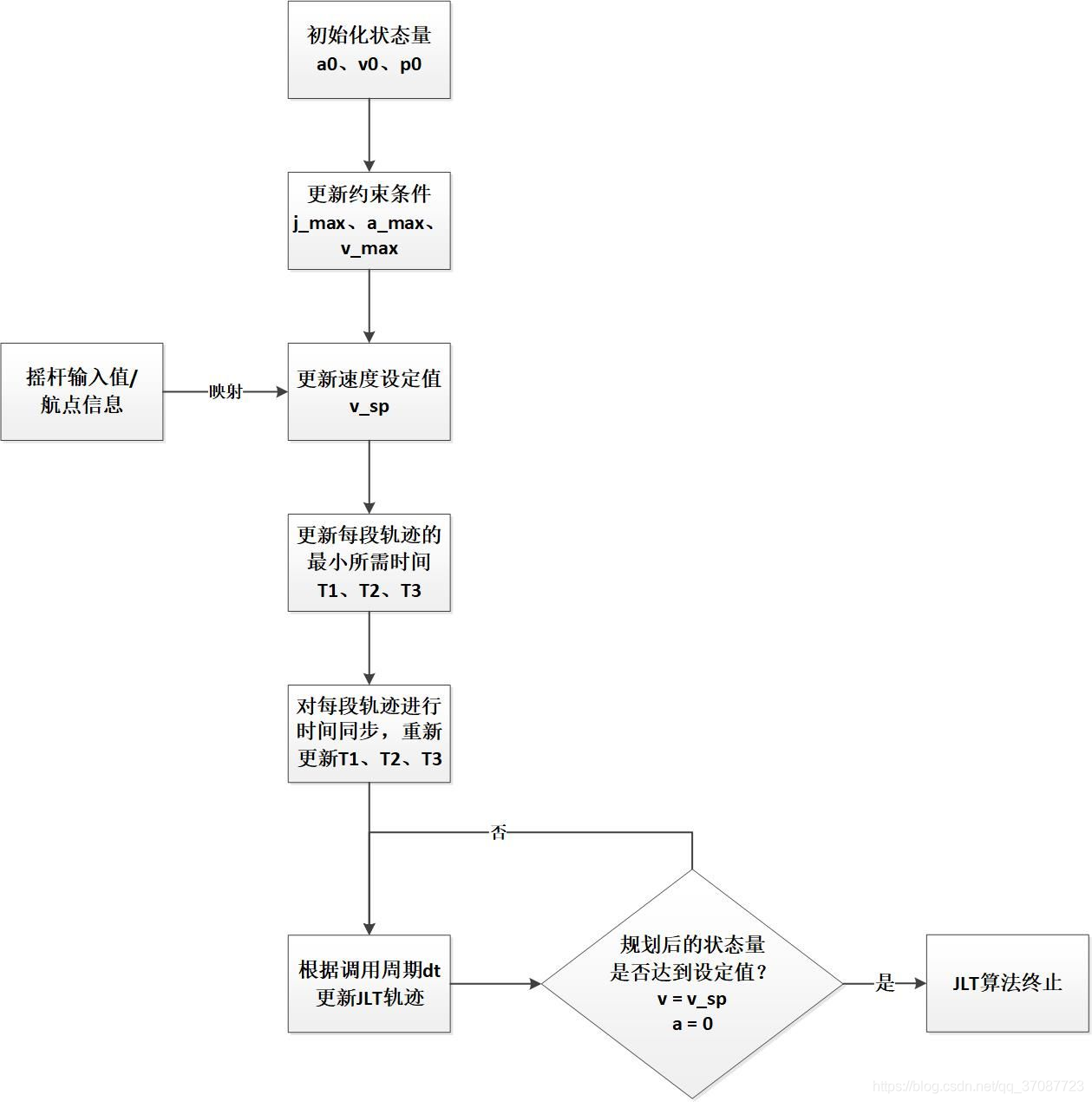

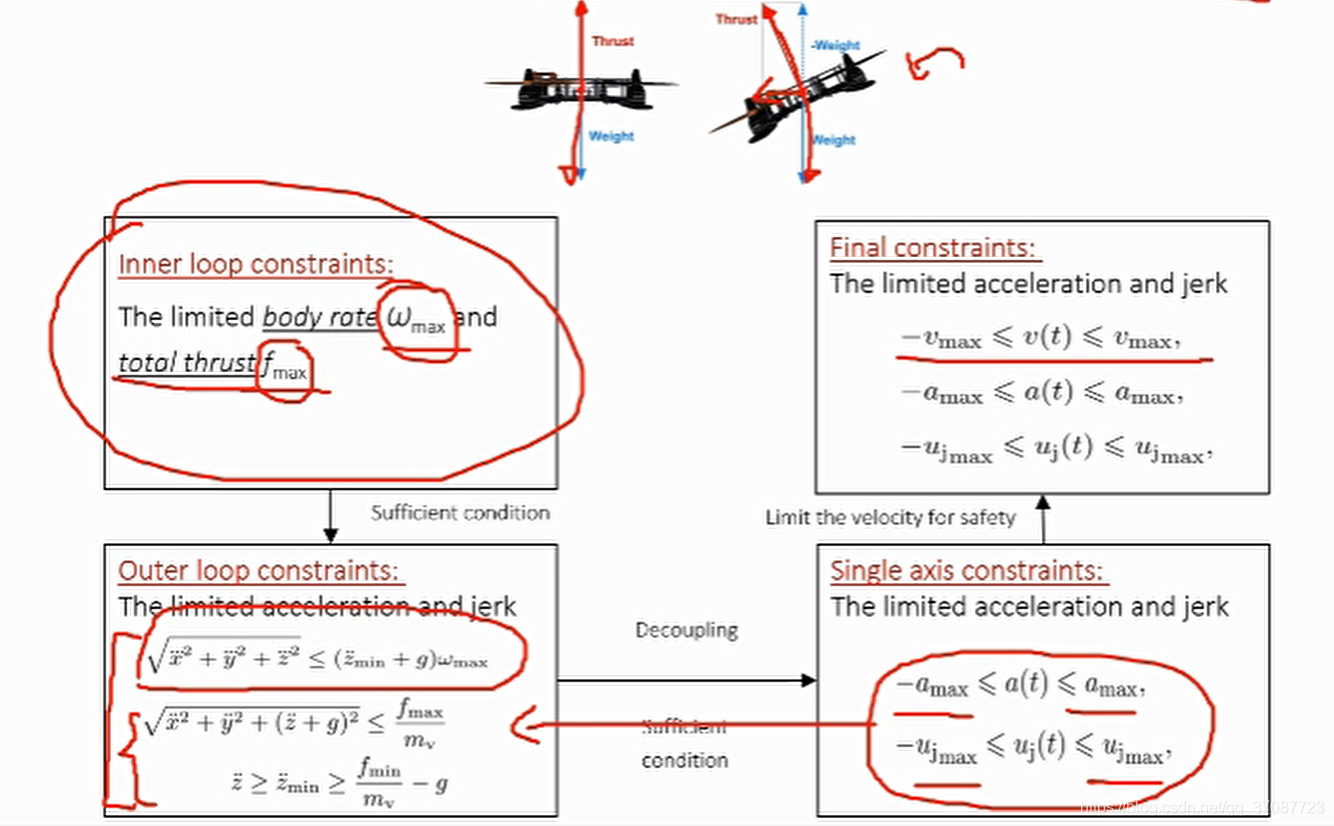
第二步中需要内环约束映射到外环的原因是由于运动规划器针对外环操作
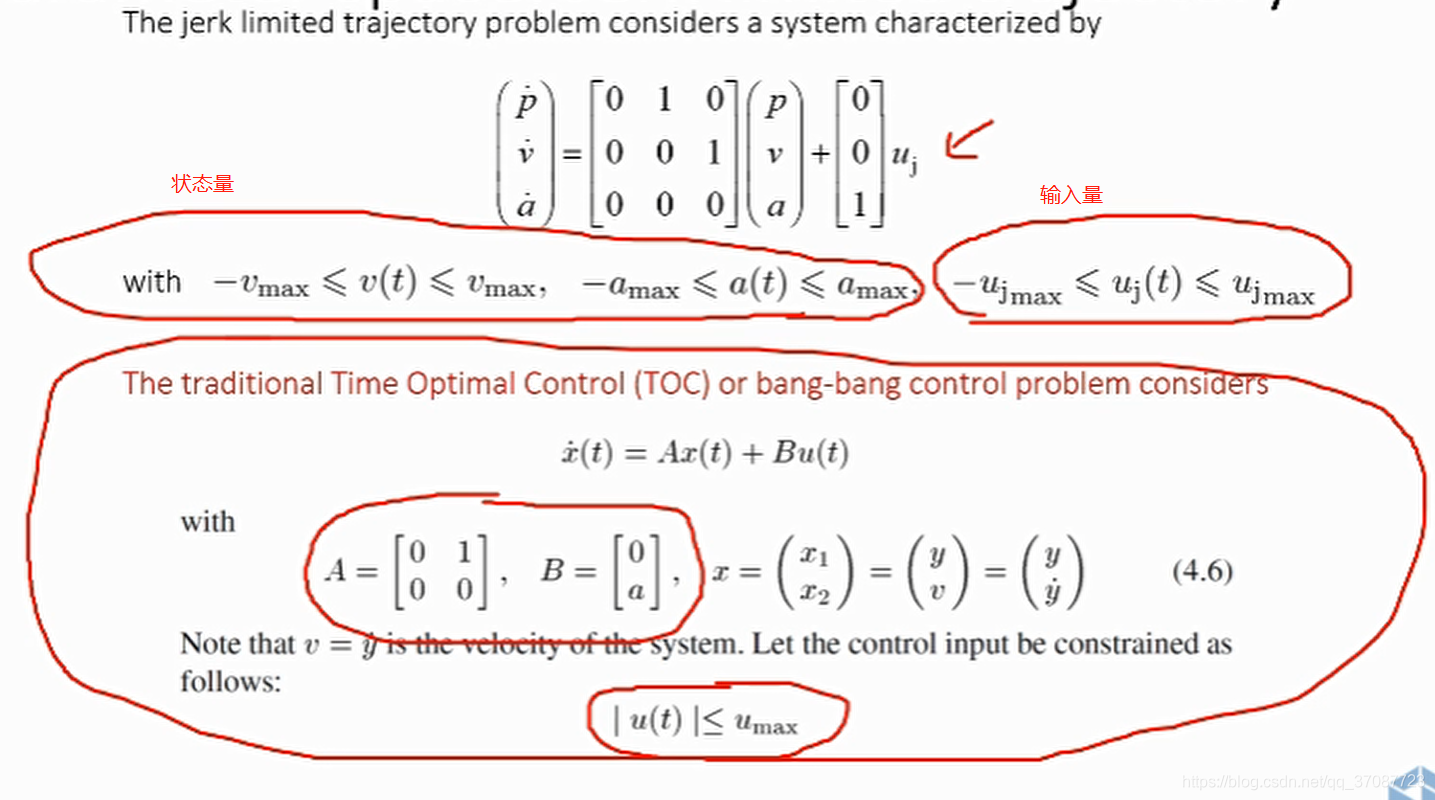
下图上部是三阶积分器模型
使用时最优控制
不仅能对输入量进行控制,也能状态量进行控制
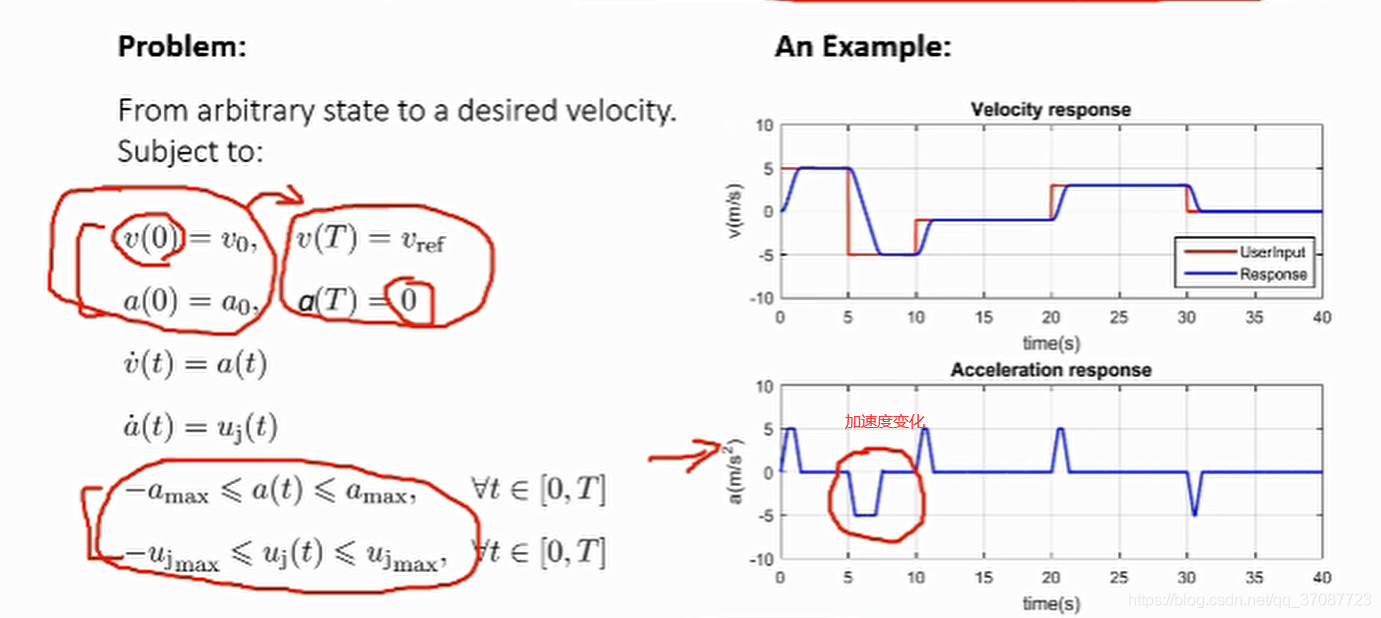
结果表明,轨迹主要由u=−ujmax,u=ujmax和0三段组成,[论文](On-Line Trajectory Generation in Robotic Systems)
如何求解?
通过观察,加速度图像要么是三角形,要么是梯形,目标是使得加速度图像的面积等于 要求的速度变化量
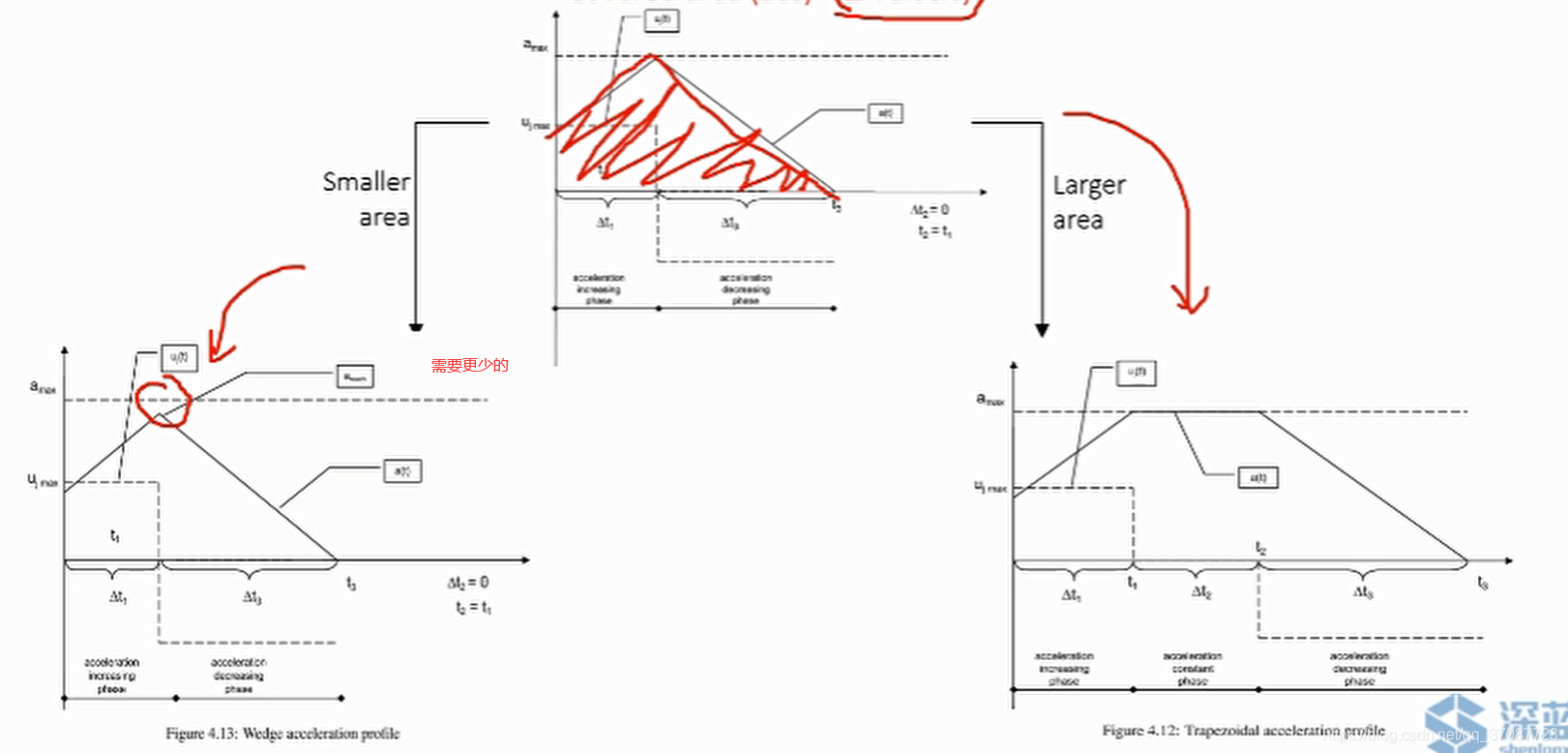
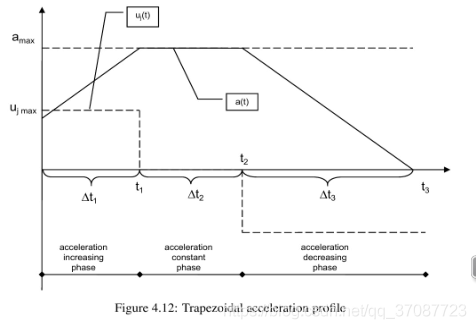
容易求出一个二阶积分器,接下来是三阶积分器
从任意状态到期望点
速度,位置曲线越平滑越有利于飞行
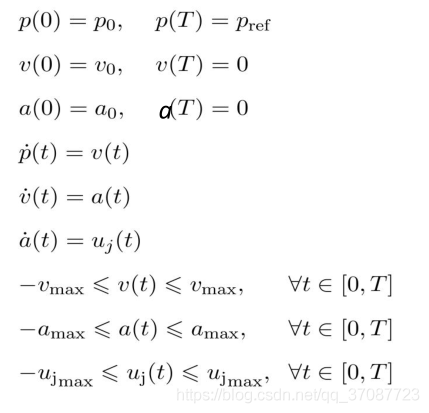
例子
此时对应的是位置的变化
先加速到最大,然后减速,需要求解加速时间
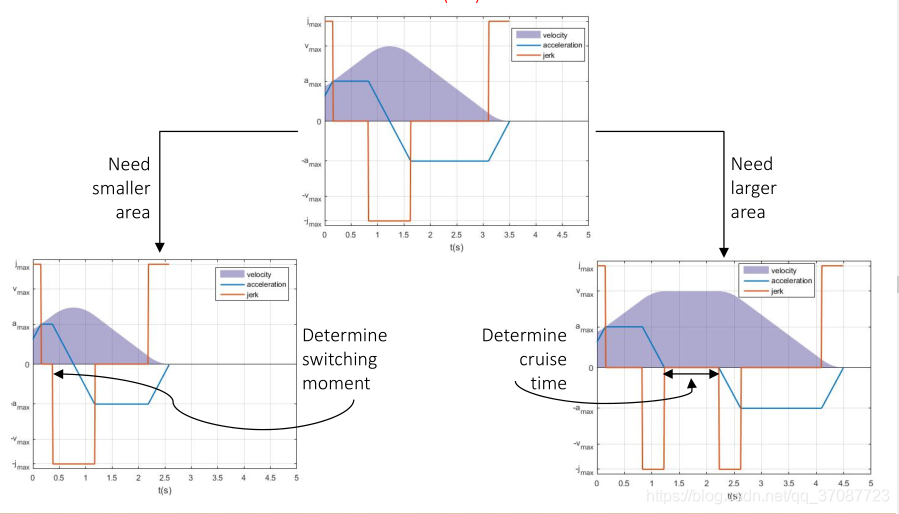
限制在安全走廊问题

- 一种高效的三维速度、加速度和限jerk轨迹生成算法,对硬件要求低
- 能对变化的即时反应(环境/任务)

JLT:Non-linear MPC
environment perception
Pixelized environment
●占据地图
〇像素是否被占用
●成本地图
- 进入某个像素的代价
- 离最近障碍物的距离信息(EDT)


未知区域代价在两者之间
映射过程
- 读取传感器数据
- 更新占用地图
a.添加新的障碍
b.清洁LOS区域
3.执行EDT - 执行成本分配
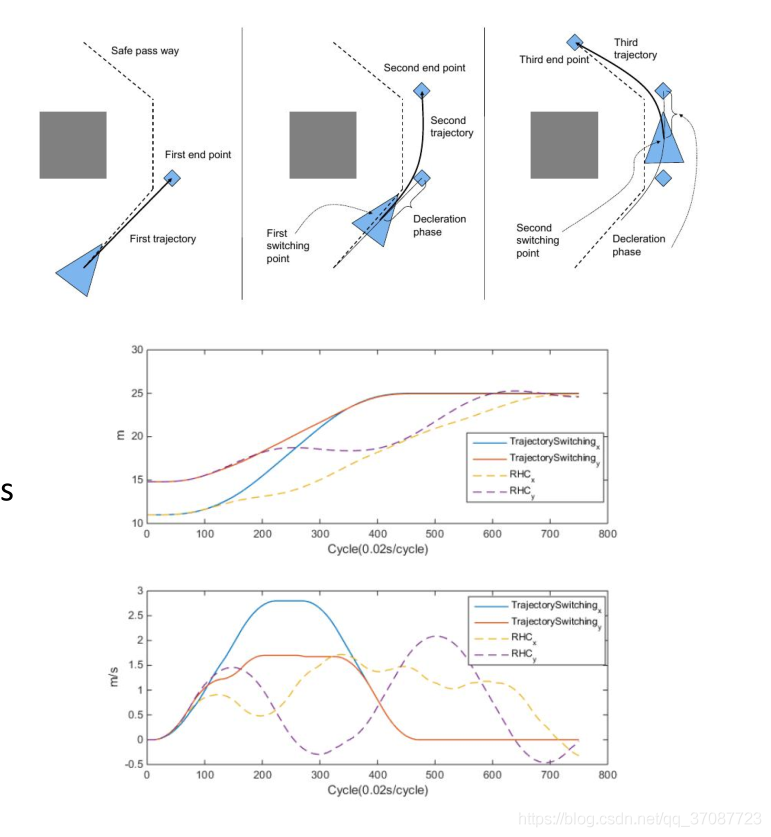
Two level guidance
把问题分成一系列的TPBVP(Two-point boundary value problem)。
•全局规划
提供一系列相互连接的线段
•轨迹规划
求解jerk有限轨迹TPBVP。
该轨迹将车辆导向线段路径上的第一个拐点Xf(每个Xf对应一条轨迹)。
它为评估提出了多种轨迹。
•评估者
评估轨迹的质量

Evaluator
检查每个轨迹的质量,不根据采样点来评分(点与点之间可能有障碍物)
•使用connected表示原始轨迹线段。
•执行DDA marching,检查每个像素覆盖的轨迹。
•找到具有最高成本价值的像素。
•根据时间评估轨迹
持续时间和清洁度
Event Manager
(事件驱动MPC!,Y确定何时更新轨迹)搭配tube 来使用,可以使得MPC的更新频率有依据,便于降低计算量
●轨迹调节
〇 持续监控当前轨迹是否安全。
●事件处理程序
〇如果当前轨迹即将结束,触发一个重新规划事件
〇如果当前轨道不安全,则触发重新规划应急事件
●节省计算能力,飞行更平稳
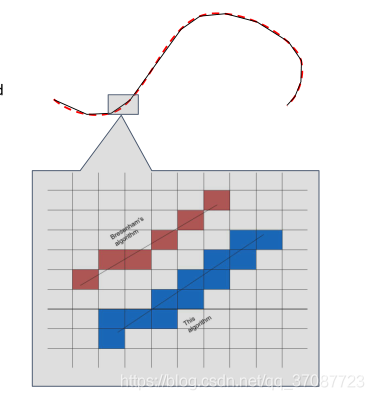
对比图
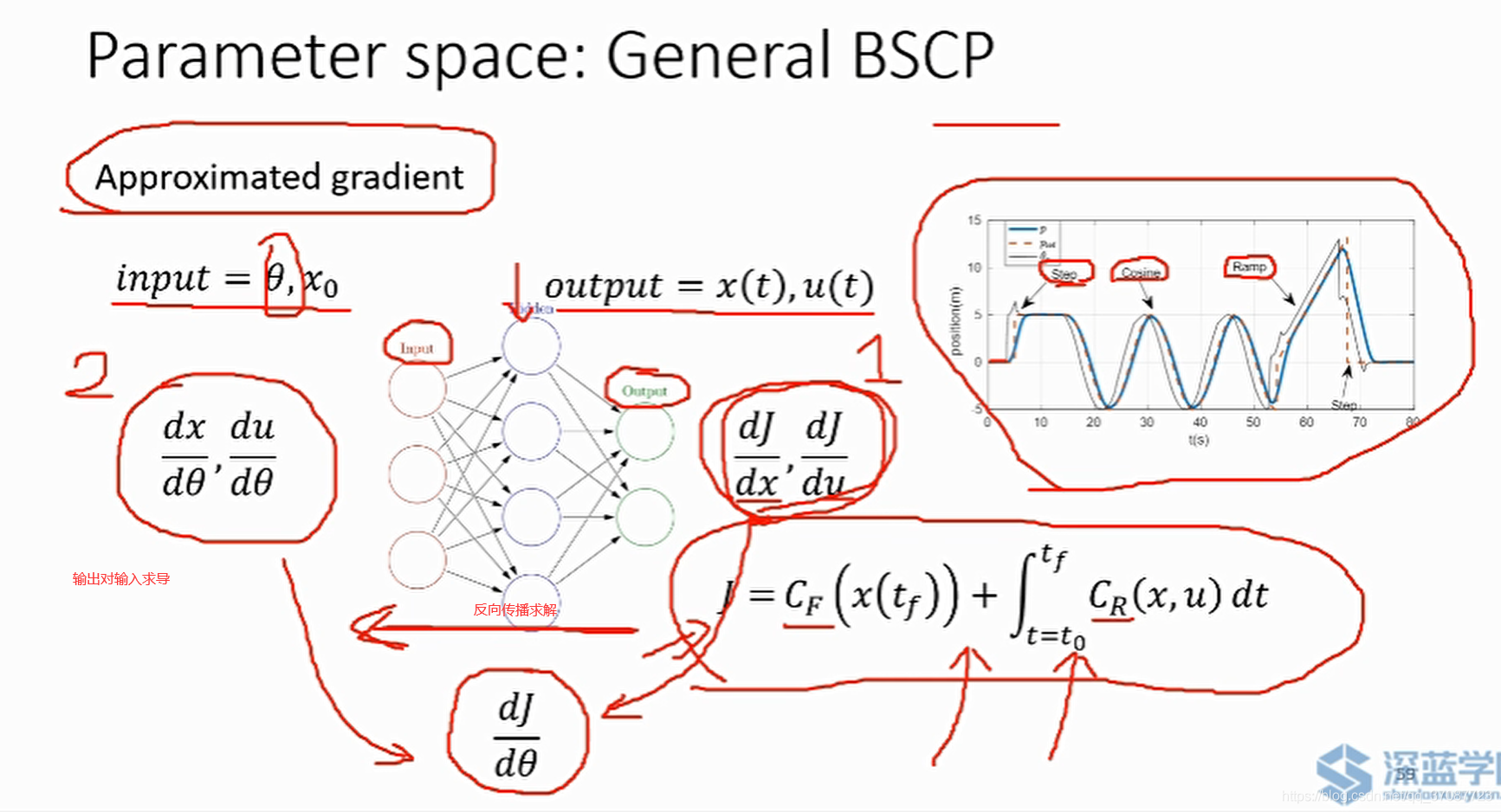
cost function and constraints(由于本来就满足前三个约束,只需要关注最后一个)
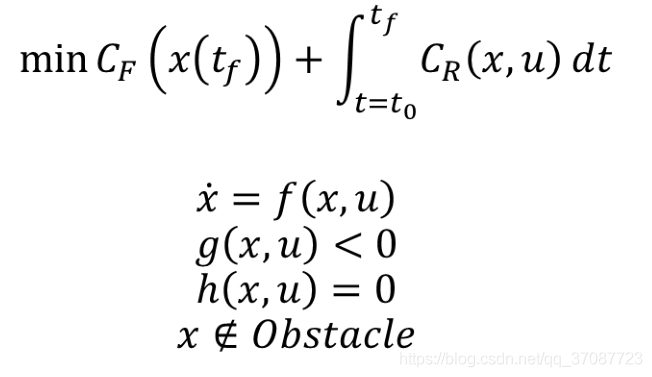
硬约束:
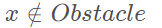
软约束(非线性)
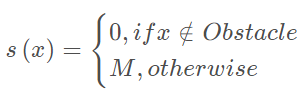
running cost
组成:轨迹到目标点距离,轨迹平滑(惩罚过大的输入),障碍物约束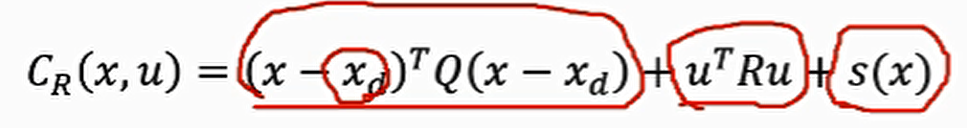
end cost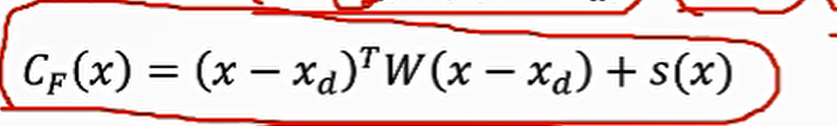
x0,xf−>x(t)
x_0,固定,确定x_f,但却很难得到关于xf 的梯度,所以这是一个缺乏梯度的优化函数(由于非线性软约束的存在),而且在对其轨迹进行评分时函数是不连续粒子群优化


在地图中散xf 点,对到达的终点x f 的轨迹进行评分,最终收敛到一个点,其自身存在速度,关乎下一次到达的点
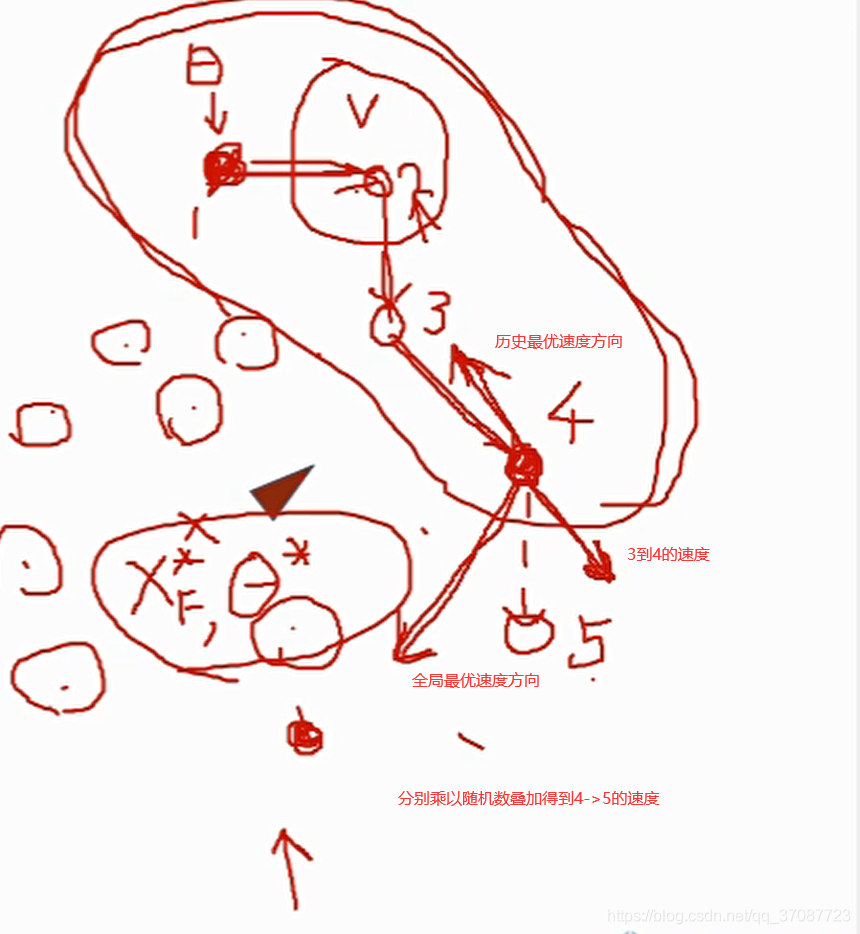
通过不断的迭代,得到最优的final point
由于θ ∗的牵引到达最优点
每一次MPC通过PSO找到最优的终点.
飞行效果

JLT仅仅适应于三阶积分器,不适应于汽车模型,固定翼等等,那么需要更一般的算法
Parameter space: General BSCP
一般的BVP问题:
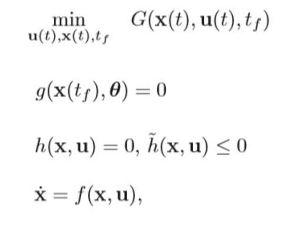
终止条件,第二个,
动力学约束![]()
通常需要数值优化(数值解)。
有时可以通过控制器来达到相同效果.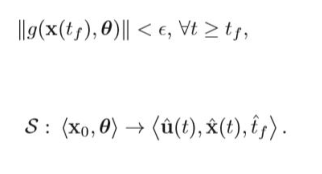

[论文](Model Predictive Local Motion Planning With Boundary State Constrained Primitives)

问题说这个系统是一个黑箱的系统?
对于这种黑箱系统,需要PSO这类算法,但是需要采样许多点才能够收敛,系统实时性慢,
那么可以将

数值优化解用神经网络来近似参数 ,不需要梯度的方法.
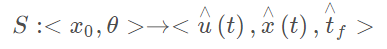
更新x0 。
优化
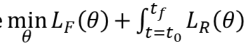
得到θ ∗
使用NN估计输入u,作为参考量,输出轨迹,不准,
将θ ∗带入原来的BVP,解出来,
- List item
不需要费时的数值解
- 直接用输入

网络的大小和训练细节
估测梯度
PSO
PSO: 10个粒子,10次迭代。VS均匀采样:100个粒子1次迭代
PSO相对于均匀采样轨迹更平滑
Unicycle model

对于更大的差速小车,需要有线加速度和角加速度,二阶系统。
Dynamic window approach

- 给定一组期望的线速度,角速度
- 预测的未来轨迹是一段圆狐
- 根据障碍物距离,无碰撞距离,与目标的相对距离等计算轨迹。
- 给每个轨迹评分
- 选择分数较高的轨迹
详见博客
每次DWA算法都需要在(红色的窗口,但不能在深灰色区域)找到一个最优的速度和角速度,限制选择范围是因为电机速度不能大的跳变。
Second order unicycle


对线性加速度和角加速度有额外的限制。
给定一对预期的线速度和角速度,未来的轨迹不再是一个圆弧。
需要一个底层控制器用于调节线速度/角速度到期望的值。
compare DWA with our approach
| DWA | MPC |
|---|---|
| 限制在一阶小车 | 处理二阶也可以 |
| 轨迹预测为一个圆弧,对于高阶可以用forward simulation | 对于高阶可以用forward simulation或者神经网络 |
| 找到优化轨迹方法,也就是最优的速度,如前文所述 | 粒子群优化,比DWA均匀采样的更优 |
Homework
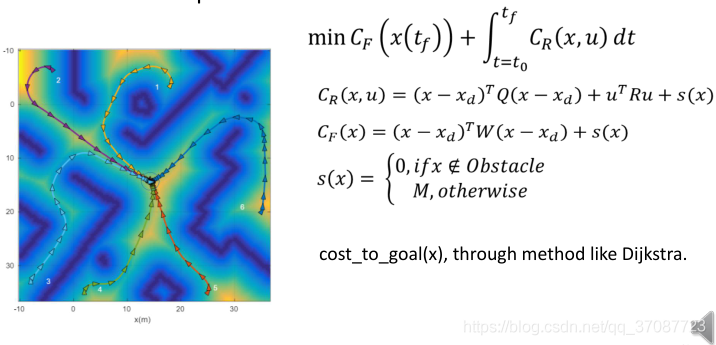
Previously, we have discussed how to design a quadratic programming based MPC to allow a single-axis triple integrator to travel from an arbitrary state to the centre of the state space, a.k.a with zero position,velocity and acceleration.Now please design a quadratic programming based MPC to track conical spiral for a 3-axis triple integrator (basically a quadrotor model).
向下速度减弱一些,防止失速
作业二
二阶模型
评价函数已经给出了,任务从任意的初始状态到地图的中心。



