5轨迹优化

Introduction

为什么需要平滑轨迹呢

•适合自主移动。
•速度/高阶动力学状态不能突变。
•机器人不能在转弯时停下来。
•节约能源。

为啥需要轨迹生成/优化

问:我们有前端(寻径)，为什么必须有后端（轨迹生成）?
见上
问:前端是动态可行的，为什么后端必须要存在
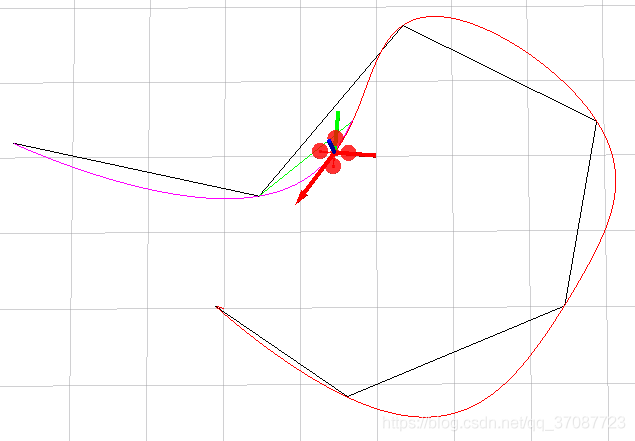
如蓝色为优化的轨迹，更适合汽车的运动

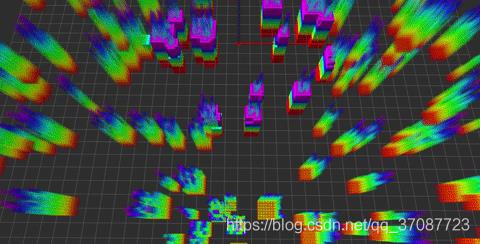
平滑的轨迹生成

边界条件:起点、目标位置(方向)
中间条件:中继节点waypoint，位置(方向)
- 通过路径规划(A*， RRT*等)可以找到路标点（中继节点）
平滑度评价函数
- 通常转化为 "最小化输入变化率" 的问题

Minimum Snap Optimization

微分平坦（Differential Flatness）

四旋翼飞行器的状态和输入可以写成代数函数组合，也就是四种仔细选择的平面输出及其导数

能够自动生成轨迹
平坦输出空间中的任何光滑轨迹(具有合理有界导数（不会快速发散）)都可以被欠驱动的四轴飞行器跟随。
a possible choice
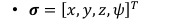
$Ψ$ 偏航角
$θ$ 俯仰角
$\phi$ 横滚角
平坦输出空间的轨迹
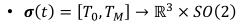
T0，TM时间段，定义R³×SO(2)
Quadrotor dynamics

Nonlinear dynamics

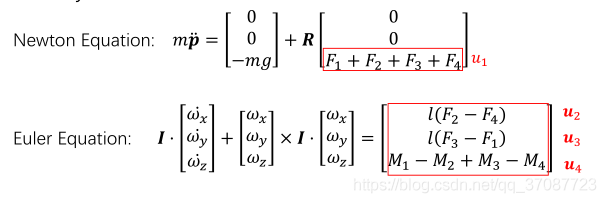
- 转动方程 Euler Equation
- where R 旋转矩阵，w世界坐标系 B 物体坐标系 l力臂长度
  note : 无人机产生的推力方向只能够垂直于桨叶平面
quadrotor states
位置，方向，线速度，角速度（在物体坐标系下)

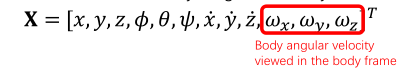
需要高维空间的变量整理成低维空间的变量，主要的思路是通过，位置和一个偏航角去表示这12个状态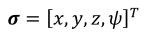
运动方程：等价于上面两个方程 Newton &Euler Equation
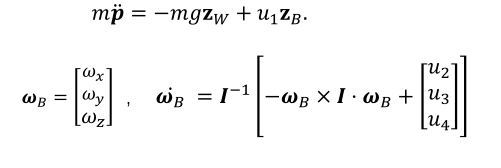
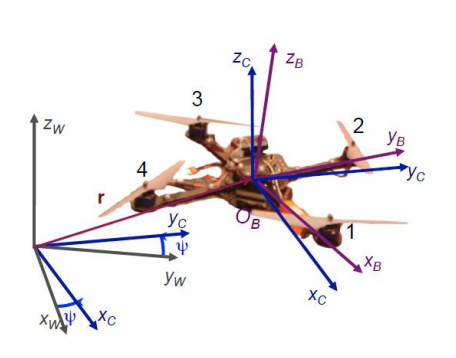
note:位置、速度和加速度只是平面输出的导数，一般选择加速度做优化，机器人的姿态没有优化
[参考论文](Minimum Snap Trajectory Generation and Control for Quadrotors , Daniel Mellinger and Vijay Kumar)

Orientation（方向）

zB为合加速度的单位向量，t使用x , y , z 的二阶导和重力加速度表示

Angular velocity（角速度）

Summary

Close the planning-control loop

在这里插入图片描述

通过轨迹规划得到的位置信息p_des速度信息(位置信息的导数)，加速度信息(位置信息的二阶导)和偏航角输入位置控制器，计算出推力u 1 和姿态信息，

将姿态信息输入姿态控制器解算出三个方向的力矩u2 , u3 , u4 同完成对无人机的控制。

polynomial Trajectories

Minimum-snap

Smooth 1D Trajectory

在这里插入图片描述

可以参看路径跟踪-曲线插值法文章理解

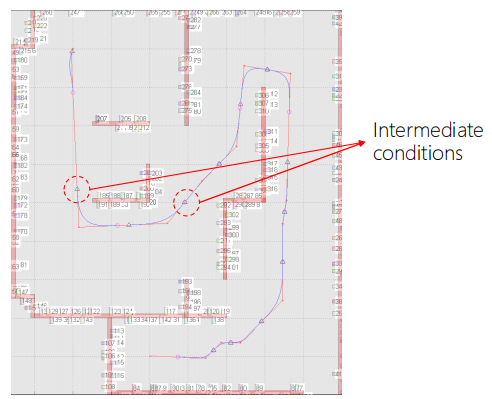
平滑直线段的角。
•首选恒速运动。
•首选零加速度。
需要特殊处理短段。

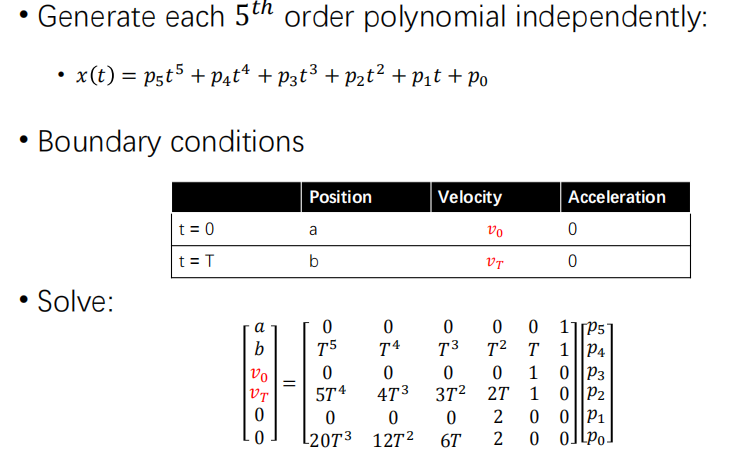
Optimization-based Trajectory Generation

在平面输出空间中显式地最小化某些导数

translation(线性方向)

minimum snap trajectory 可以理解为最小化加加加速度轨道
关于牛顿第二定律深度理解：
Jerk: 所受力的变化率。（如每秒增加一牛顿）
snap: 所受力的变化率的变化。（如前一秒增加一牛顿，接下来一秒增加两牛顿，第二秒受力与最初相比增加了三牛顿）
最小snap，就让jerk变化比较小。如果snap为0，就代表每秒加速度稳定增加（受力稳定增加）
在平面输出空间中显式地最小化某些导数

•最小冲击:最小角速度，良好的视觉跟踪
•最小弹跳:最大差动推力，节省能源
NOTE：如果是针对minimum jerk，则需要提供位置，速度，加速度3个状态量。如果只考虑起点和终点，则有2 ∗ 3 = 6 个状态。同时考虑多项式形式包含有x0(也就是常数项），所以最终多项式的次数N=5
同样的道理，如果minimum snap，则需要提供位置，速度，加速度，以及加速度变化率，4个状态量。所以N = 2 ∗ 4 − 1 = 7 。

Note2：如果考虑多段的情况，例如K段，则minimum jerk ，需要 (k-1) +3 +3= k+5 , 这里只要求能够连续的到达中间点，至于以怎样的速度，怎样的加速度到达这个点，是优化出来的，不属于约束。、

假设每一段的阶数为N ,则每一段轨迹所能提供的自由度为N+1。N阶多项式可以提供N次导数，加上原多项式，即为N+1。所以，总计（N+1）*k.
(N+1)*k>= k+5. 则 N_{min} = 5/k. 表明段数越多，则提供的阶次越低。
每一个分段都是多项式；每个分段的多项式都是相同的阶次，这样对于问题的求解比较简单；每一段的时间间隔都是已知的(也可以不已知,但那就是优化时间间隔的问题了)

Multi-segment minimum-snap trajectory

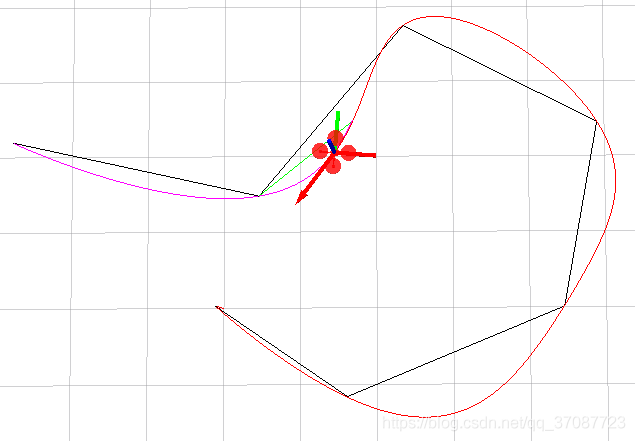
一个多项式曲线过于简单，一段复杂的轨迹很难用一个多项式表示，所以将轨迹按时间分成多段，每段各用一条多项式曲线表示，形如：

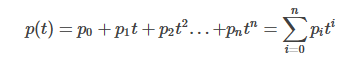
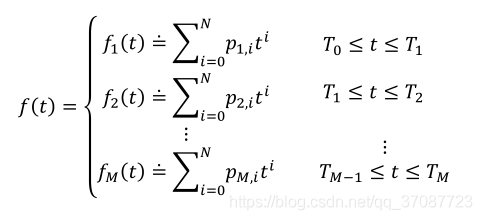
M为轨迹的段数，i指一段的第几项(0,N)
Minimum Snap的最小化目标函数为snap（jerk的导数，jerk为加速度的导数），对于一段轨迹，最小化jerk选择的阶数为5(2x3-1），3个未知量分别为位置、速度、加速度)，最小化snap选择的阶数为7(2x4-1），4个未知量分别为位置、速度、加速度、jerk)。实际过程中，考虑最坏情况，k段距离阶数的选择与1段轨迹相同。

每一段都是一个多项式。
•不需要确定阶次，但保持相同的阶次可以使问题更简单。
•必须知道每个段的时间长度!

constraints

导数约束
局部连续约束

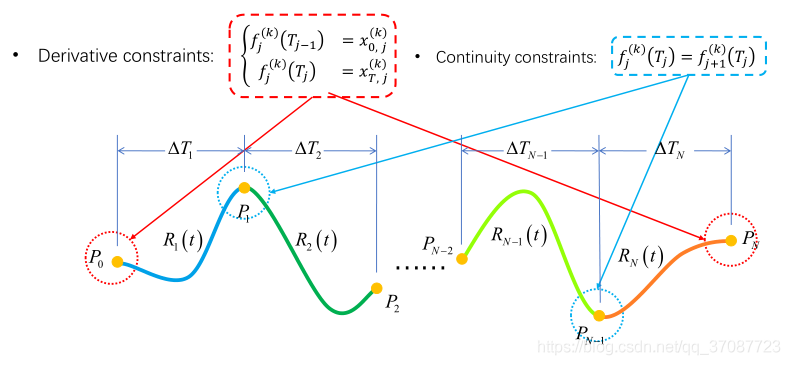
different timeline

时间分配的方法：匀速分配或梯形分配，假设每段polynomial内速度满足匀速或梯形速度变化，根据每段的距离将总时间T分配到每段。
这里的轨迹分段和时间分配都是初始分配，在迭代算法中，如果corridor check和feasibility check不满足条件，会插点或增大某一段的时间
用的是后一种

Objective function

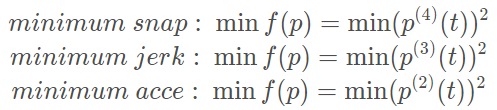
其中第j段多项式段的成本函数：最终要将整个路径（分成多段）的成本函数最终形式表示出来（主要得到Q）

function Q = getQ(n_seg, n_order, ts)
    Q = [];
    for k = 1:n_seg
        Q_k = zeros(n_order + 1, n_order + 1);
        %#####################################################
        % STEP 1.1: 计算第k段的矩阵Q_k 
        for i = 4:n_order
            for j = 4:n_order
                Q_k(i+1,j+1) = factorial(i)/factorial(i-4)*factorial(j)/factorial(j-4)/(i+j-n_order)*ts(k)^(i+j-n_order);
            end
        end
        Q = blkdiag(Q, Q_k);
    end
end

导数约束(A 的构建)

两段之间的连续性约束：

在未给出特定导数时，确保轨迹段之间的连续性

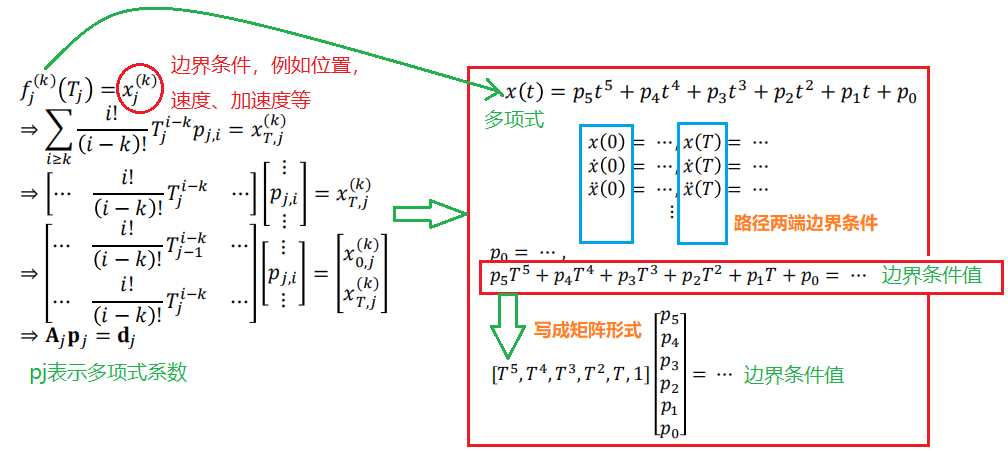
整理得到最终的约束问题，每一段都是相关的二次型；从而转化为标准的凸优化问题

A_e_q∗P=d_e_q（b_eq）

function [Aeq beq]= getAbeq(n_seg, n_order, waypoints, ts, start_cond, end_cond)
    n_all_poly = n_seg*(n_order+1);
    %#####################################################
    % p,v,a,j 的起点约束, 
    Aeq_start = zeros(4, n_all_poly);
    % STEP 2.1: write expression of Aeq_start and beq_start
    Aeq_start(1:4,1:8) = getCoeffCons(0);
    beq_start =  start_cond';
    
    %#####################################################
    % p,v,a,j 的终端约束
    Aeq_end = zeros(4, n_all_poly);
    t = ts(end);
    Aeq_end(1:4, end-7:end) = getCoeffCons(t);
    beq_end =  end_cond';
    
    %#####################################################
    % 中点的位置约束
    Aeq_wp = zeros(n_seg-1, n_all_poly);
    beq_wp = zeros(n_seg-1, 1);
    
    for k = 0:1:n_seg-2
        beq_wp(k+1, 1) = waypoints(k+2);
        coeff = getCoeffCons(ts(k+1));
        Aeq_wp(k+1, 1+k*8:8+k*8) = coeff(1, :);  
    end
    
    %#####################################################
    % 连续性约束
    Aeq_con_p = zeros(n_seg-1, n_all_poly);
    beq_con_p = zeros(n_seg-1, 1);
    Aeq_con_v = zeros(n_seg-1, n_all_poly);
    beq_con_v = zeros(n_seg-1, 1);
    Aeq_con_a = zeros(n_seg-1, n_all_poly);
    beq_con_a = zeros(n_seg-1, 1);
    Aeq_con_j = zeros(n_seg-1, n_all_poly);
    beq_con_j = zeros(n_seg-1, 1);
    Aeq_con = [Aeq_con_p; Aeq_con_v; Aeq_con_a; Aeq_con_j];
    beq_con = [beq_con_p; beq_con_v; beq_con_a; beq_con_j];
    
    for k = 0:1:n_seg-2 
        Aeq_con(1+4*k:4+4*k,1+8*k:8+8*k) = getCoeffCons(ts(k+1));
        Aeq_con(1+4*k:4+4*k,1+8*(k+1):8+8*(k+1)) = -getCoeffCons(0);            
    end
    
    %#####################################################
    % 构造约束矩阵
    Aeq = [Aeq_start; Aeq_end; Aeq_wp; Aeq_con];
    beq = [beq_start; beq_end; beq_wp; beq_con];
end
function coeff = getCoeffCons(t)
    coeff = [1,  1*t,  1*t^2,  1*t^3,  1*t^4,  1*t^5,  1*t^6,  1*t^7;
             0,  1,    2*t,    3*t^2,  4*t^3,  5*t^4,  6*t^5,  7*t^6;
             0,  0,    2,      6*t,    12*t^2, 20*t^3, 30*t^4, 42*t^5;
             0,  0,    0,      6,      24*t,   60*t^2, 120*t^3,210*t^4];
end

%main 
clc;clear;close all;
path = ginput() * 100.0;

n_order       = 7;% order of poly
n_seg         = size(path,1)-1;% segment number
n_poly_perseg = (n_order+1); % coef number of perseg

ts = zeros(n_seg, 1);
% calculate time distribution in proportion to distance between 2 points
% dist     = zeros(n_seg, 1);
% dist_sum = 0;
% T        = 25;
% t_sum    = 0;
% 
% for i = 1:n_seg
%     dist(i) = sqrt((path(i+1, 1)-path(i, 1))^2 + (path(i+1, 2) - path(i, 2))^2);
%     dist_sum = dist_sum+dist(i);
% end
% for i = 1:n_seg-1
%     ts(i) = dist(i)/dist_sum*T;
%     t_sum = t_sum+ts(i);
% end
% ts(n_seg) = T - t_sum;

% or you can simply set all time distribution as 1
for i = 1:n_seg
    ts(i) = 1.0;
end

poly_coef_x = MinimumSnapQPSolver(path(:, 1), ts, n_seg, n_order);
poly_coef_y = MinimumSnapQPSolver(path(:, 2), ts, n_seg, n_order);


% display the trajectory
X_n = [];
Y_n = [];
k = 1;
tstep = 0.01;
for i=0:n_seg-1
    %#####################################################
    % STEP 3: get the coefficients of i-th segment of both x-axis
    % and y-axis
    for t = 0:tstep:ts(i+1)
        X_n(k)  = polyval(Pxi, t);
        Y_n(k)  = polyval(Pyi, t);
        k = k + 1;
    end
end
 
plot(X_n, Y_n , 'Color', [0 1.0 0], 'LineWidth', 2);
hold on
scatter(path(1:size(path, 1), 1), path(1:size(path, 1), 2));


function poly_coef = MinimumSnapQPSolver(waypoints, ts, n_seg, n_order)
    start_cond = [waypoints(1), 0, 0, 0];
    end_cond   = [waypoints(end), 0, 0, 0];
    %#####################################################
    % STEP 1: compute Q of p'Qp
    Q = getQ(n_seg, n_order, ts);
    %#####################################################
    % STEP 2: compute Aeq and beq 
    [Aeq, beq] = getAbeq(n_seg, n_order, waypoints, ts, start_cond, end_cond);
    f = zeros(size(Q,1),1);
    poly_coef = quadprog(Q,f,[],[],Aeq, beq);
end

Convex Optimization

Convex function and convex set

一个函数是严格凸函数当且仅当条件二和x = y时才取等号

参考自：Convex Optimization,Daniel Palomar,HKUST

如果在一个集合任意连接一条线，如果都在集合内，那便是凸集

优化与凸优化

师曰:将一个问题转化一个凸优化问题没有系统化方法
凸优化问题求解

范围：SOCP>QCQP>QP SOCP>LP

SDP可以覆盖前面所有问题，一般planning问题转化到
上面几个问题便可以求解了

MiniMum-snap求闭式解

Decision variable mapping

优化变量的映射

多项式轨迹的直接优化是数值不稳定的，对多项式系数p，可以针对多个点（有物理意义）
首选改变变量的映射，而不是优化线段端点导数
我们有M j p j = d j ，p j = M j ^{− 1} d j， $其中𝑴j是一个映射矩阵，它将多项式系数映射到导数,优化路标点的v,a$

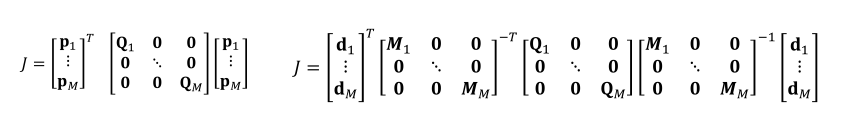
给出一个构建M矩阵的例子如下：P->M

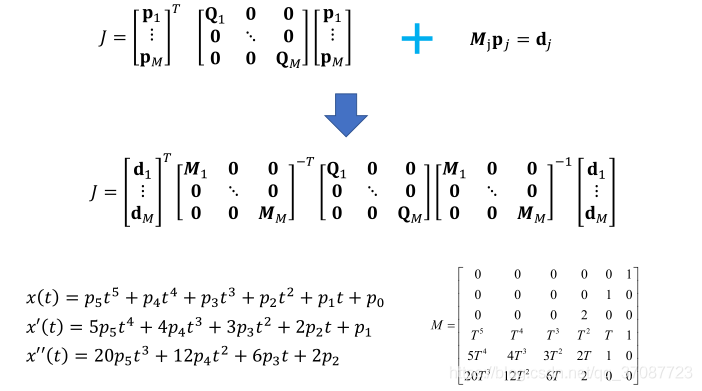
可以看出M可以通过将某段轨迹初始时刻t=0(上三行）和末尾时刻t=T（下三行）代入上式得到。
只考虑p,v,a的话,M的表达式如下

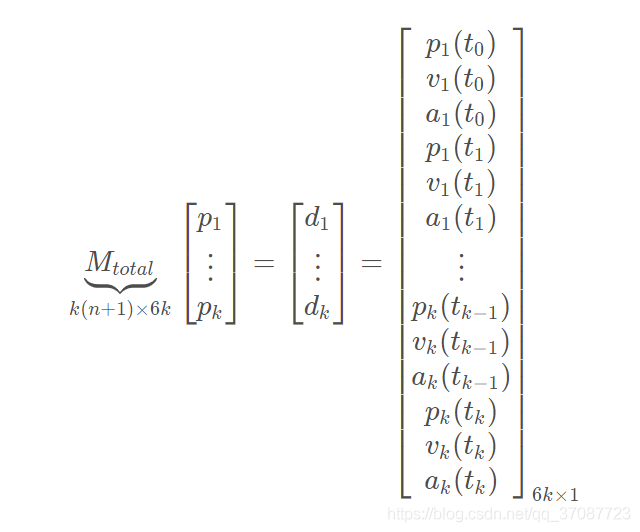
M_total是已知的（怎么构造可参见文章一种的等式约束构造方法），而 d 中只有少部分（起点、终点的pva等）是已知的，其他大部分是未知的。如果能够求出d ，那么轨迹参数可以通过 p=M⁻¹ d

参考：Polynomial Trajectory Planning for Aggressive Quadrotor Flight in Dense Indoor Environments , Charles Richter, Adam Bry, and Nicholas Roy

fixed(constrained) and free variable separation

使用选择矩阵C来分离自由(dP)和受约束(dF)变量
自由变量:未指定的导数，仅由连续性约束强制执行,即

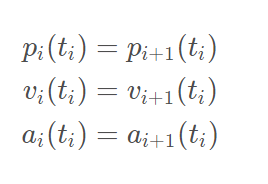
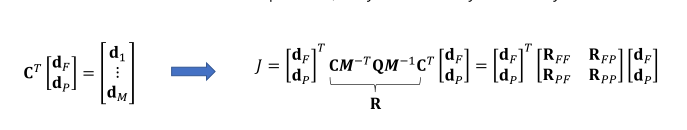
对R进行分块
转化成一个可以求解的无约束二次规划
封闭的形式:

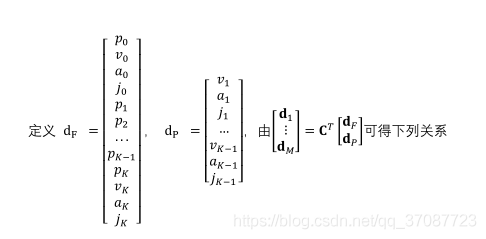
对dp求偏导为0,求J的最优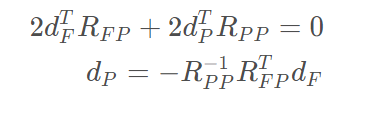
在这里插入图片描述

对于两段轨迹，构造C^T ,如图所示，相应变量对应即可映射矩阵C

参考文章

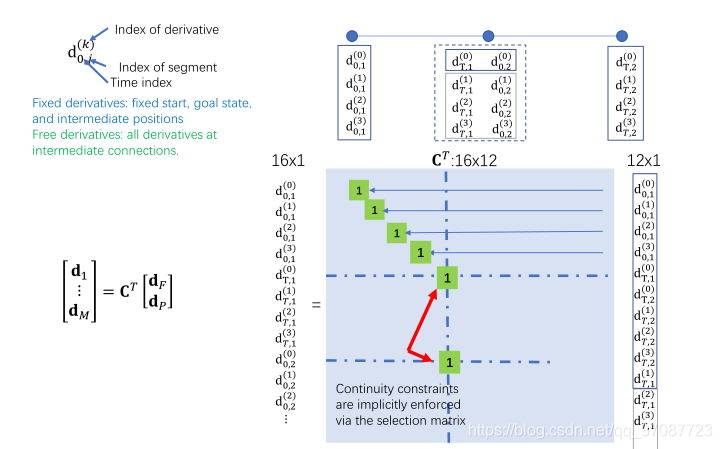
same result as convex optimization

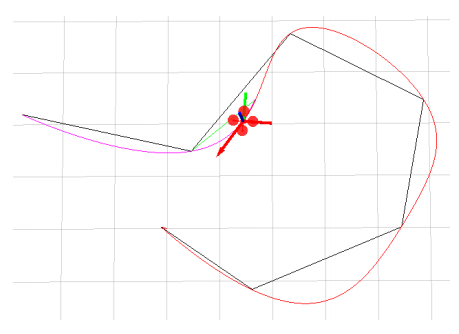
Hierachical approach（用于无人机）

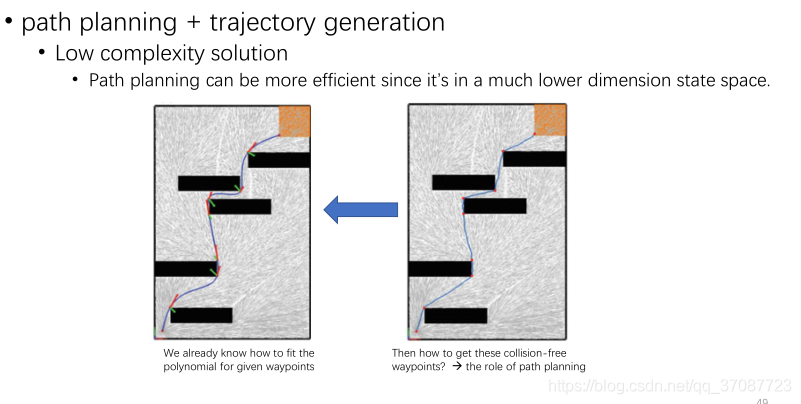
trajectory optimazition considering obstacle

发生碰撞就在中间加入路标点，不断加入直至没有碰到障碍物optimazition

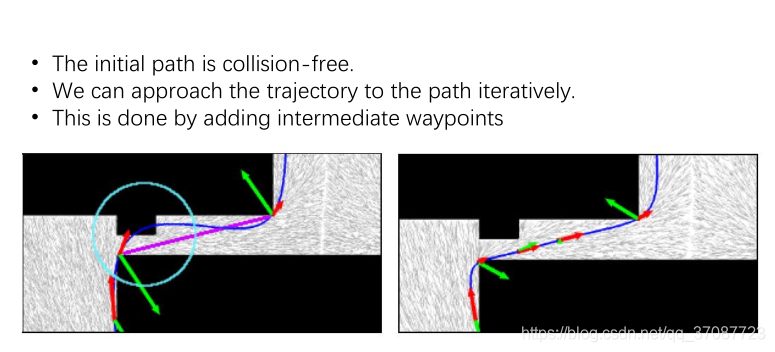
better solutions

Smooth Trajectory Generation with Guaranteed Obstacle Avoidance

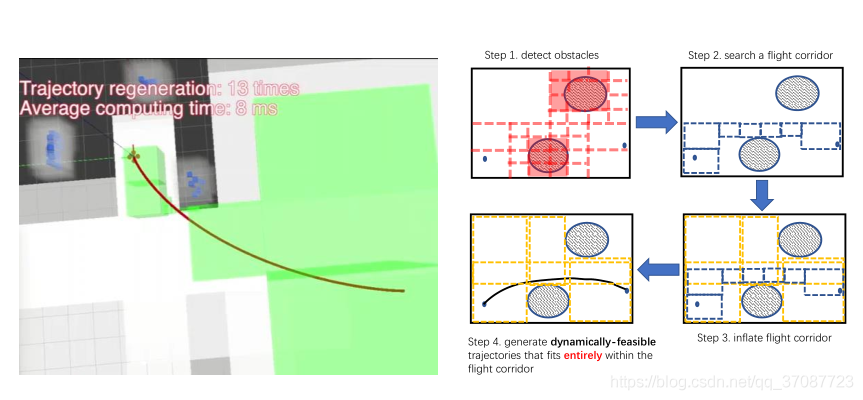
How to make constraints globally activated
迭代地检查极值并添加额外的约束。

迭代求解非常耗时。

如果严格没有可行的解决方案满足所有约束。
我们必须运行10次迭代来确定解决方案的状态

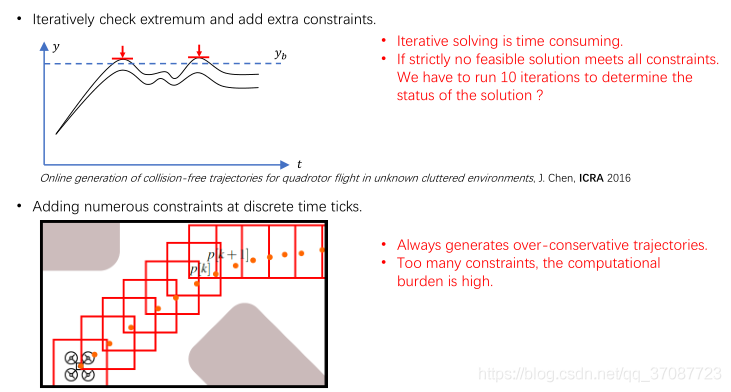
添加多个约束
总会产生过于保守的轨迹。
约束太多，计算量大。

论文
Online generation of collision-free trajectories for quadrotor flight in unknown cluttered environments , J. Chen, ICRA 2016
A hybrid method for online trajectory planning of mobile robots in cluttered environments , L Campos-Macías, RAL 2017

Implementation Details

convex solvers

我们的目标式制定一个轨迹生成问题转化为凸优化约束
许多现成的方法（off-the-shelf)能帮我们解决这个问题
根据需要选择一个求解器

CVX 数学公式直接表达
Mosek 功能全面
OOQP QP问题代码开源
GLPK LP问题

Numerical Stability

Normalization

首先是时间的标准化
在很小间隔的时间段内不生成轨迹
将短期持续时间缩放到一个（1，0）区间里的数（归一化），或者将比例因子添加到曲线的所有部分
note: 使用相对坐标轴

然后是尺度（空间）的标准化
适应条件是处于大规模的场景，如waypoint x = 100.0 m x=100.0mx=100.0m情况，使得我们仅需要考虑一个小问题（沙盒），重新调整解决方案
这两种操作大大提高了实际计算的稳定性。

Other engineering stuff

要不要3轴独立去解？通常求解要好一点
闭式解是不是更好？这个计算力较大，一般商用不会用，会用QP去求数值解
多项式是不是最优表达？如果仅是jerk 或者snap ,那么就是最优解

Time Allocation

Problem Definition

分段轨迹取决于分段时间分配。
时间分配显著影响最终轨迹。
如何合理分配时间?

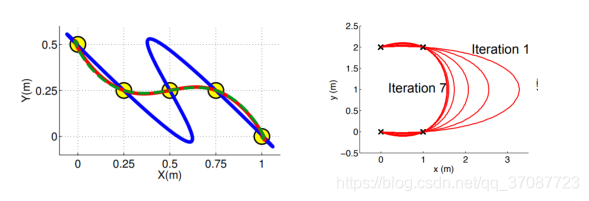
Naive solution

使用“梯形速度”时间剖面来获得每个片段的时间持续时间。
•假设在每一块上，加速到最大值，速度→减速为0。
•加速度+ 最大速度+ de-accelerate。
•使用预期的平均速度来获得每个部件的持续时间。

缺点

离最佳状态还很远。
•只获取保守的时间配置。
•对环境风格没有反应

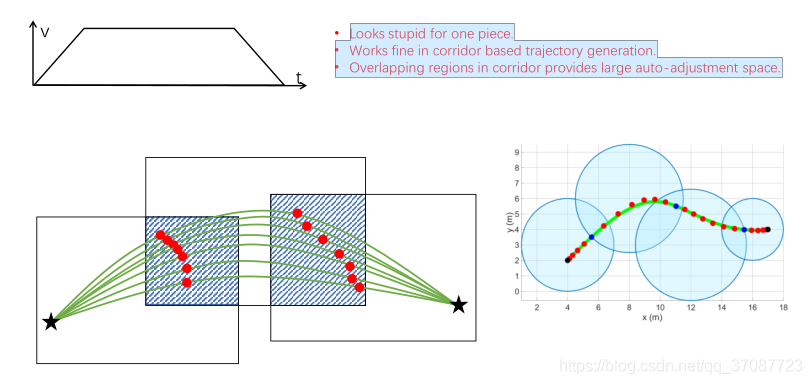
允许路标点交叠区域移动
论文：Online generation of collision-free trajectories for quadrotor flight in unknown cluttered environments , J. Chen, ICRA 2016
Fast, dynamic trajectory planning for a dynamically stable mobile robot , M. Shomin, IROS 2014

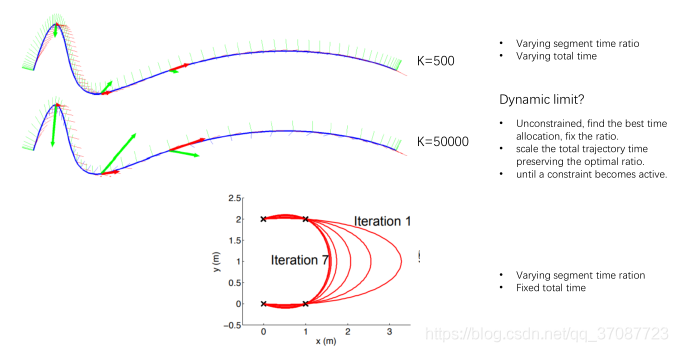
Iterative numerical solution

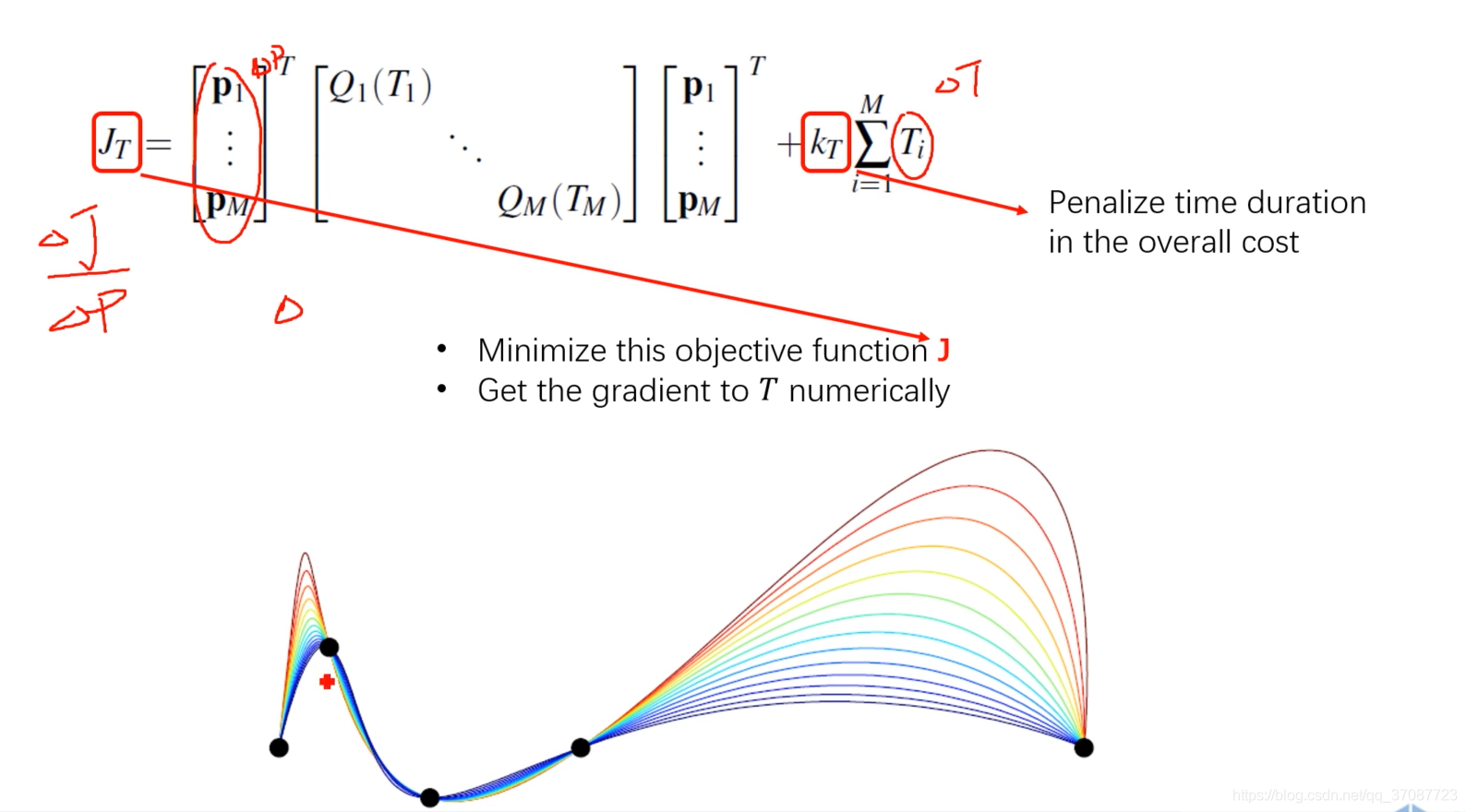
不能优化到最优解，只能够求数值的导数，计算耗时间，不能解析式求导

Homework

题目

作业1.1:在matlab中，使用“quadprog”QP求解器，写下一个Minisnap轨迹生成器
作业1.2:在matlab中，根据闭合解生成Minisnap轨迹
作业2.1:在c++ /ROS中，使用OOQP求解器，写下一个最小snap轨迹生成器
作业2.2:在c++ /ROS中，利用Eigen，基于闭式求解解生成最小snap轨迹

结果

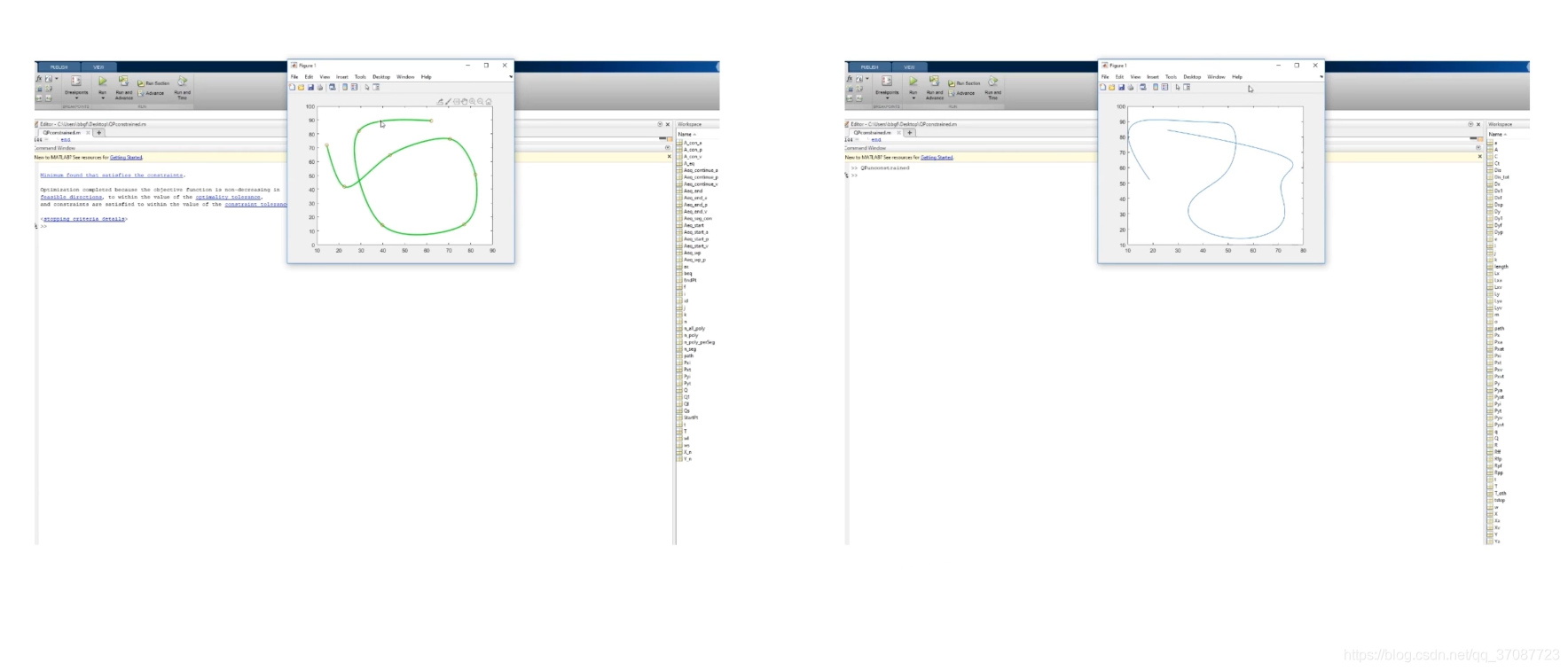
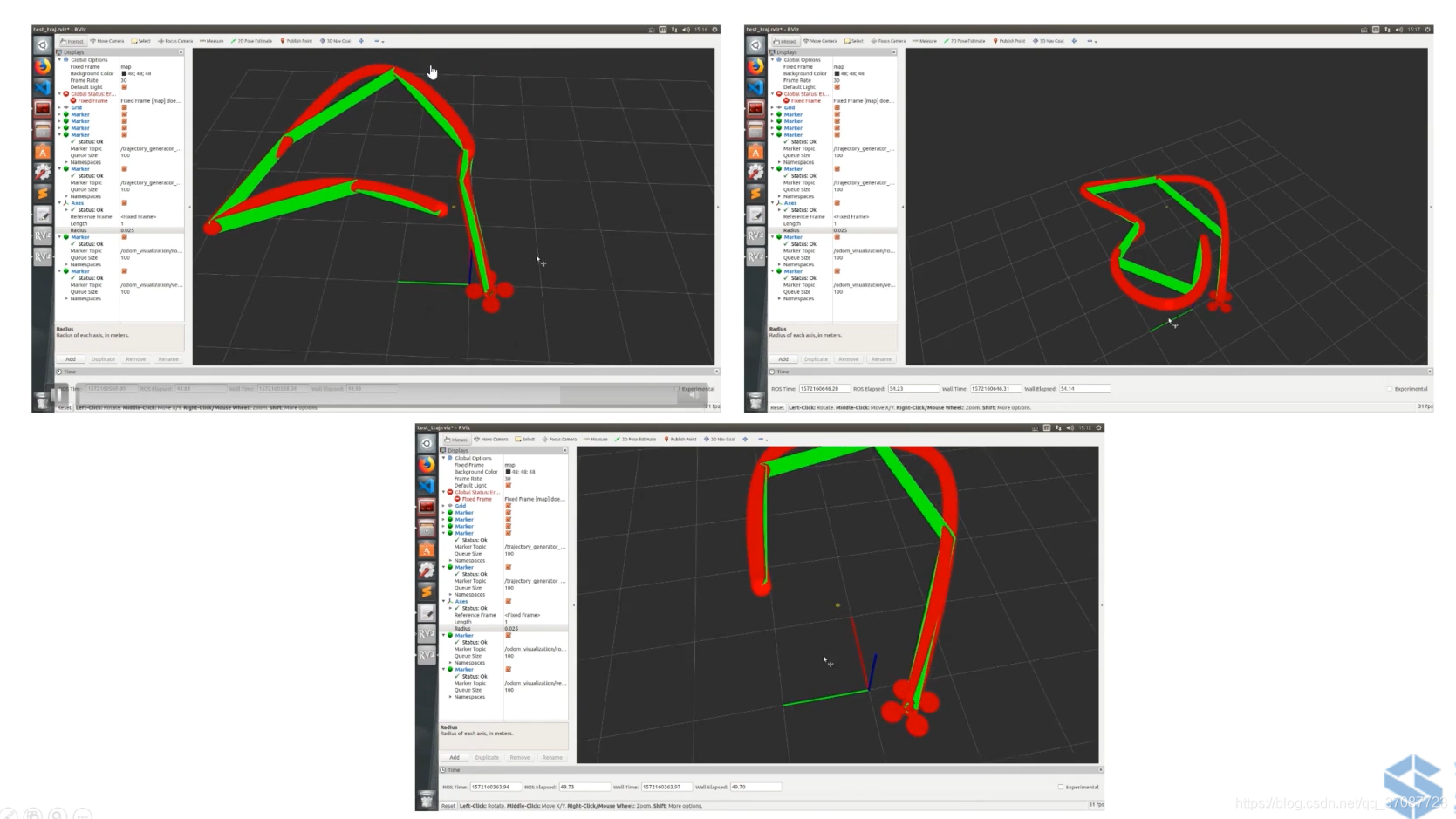
参考：https://blog.csdn.net/qq_37087723/article/details/115859746

posted @ 2021-07-31 11:03 北极星！阅读(1336) 评论(0) 收藏举报

刷新页面返回顶部

北极星！

最迷人的地方不是远方，而是在这里却没有欣赏到此刻的美丽—北极星!