4 运动动力学约束下的路径搜索
Introduction
T: 考虑机器人的动力学约束
Kinodynamic: kinematic + Dynamic
运动学规划问题是在同时受到运动学约束(如避障)和动力学约束(如速度、加速度和力的模量界限)的情况下综合机器人运动。动力学解是从时间到广义力或加速度的映射。——《动力学运动规划》,Bruce Donald, Patrick Xavier, John Canny, John Reif
不同的限制
最大力(加速度)
Y:
Straight-line connections between pairs of states are typically not valid trajectories due to the system’s differential constraints.
由于系统的微分约束,状态对之间的直线连接通常不是有效的轨迹。

- coarse-to-fine process(由粗到精)
- 轨迹只会局部规划
- 不可行路径对非完整系统没有意义
- 如大部分车不能平移,如下图所示,不能够走下面
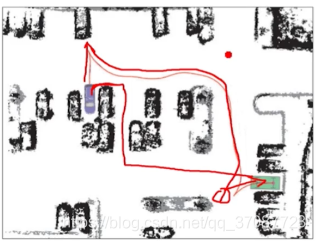
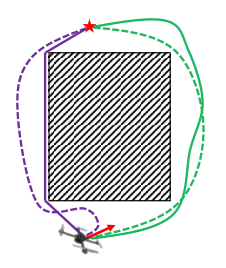
无人机的一开始的速度是在向右,但是按路径规划左边路径更短,其实应该沿着速度方向向右飞
单轮

差动轮

简化的汽车模型

r应该标记为v
Workflow
basic idea
We have many weapons to attack graph search.
•假设机器人的质量点不再令人满意。
•我们现在需要一个具有可行运动连接的图。
我们手动创建(构建)一个所有边都由机器人可执行的图。
反向,离散机器人的状态空间,连接,如栅格地图
正向。离散机器人的控制空间,如PRM
这是所有动动力规划的基本动机。
状态点阵规划(State lattice planning)是最直接的一种。
build the graph,sample in control vs state space

说明:s为状态变量,u 为控制变量
如果在控制空间没有任务导向性,在已知被控对象的条件下,固定输入的控制量u uu和积分时间T,由此进行前向积分可以得到被控对象从任意的初始状态 s_0过度到终止状态s f,前向积分可以对被控对象在任意时间T之后的状态进行预测,进而得到一系列的状态集合,这就是控制空间中的采样。由于u 和T是任意给定的,在控制空间中的采样往往没有明确的目的性,采样结果只能分布在某些状态附近,无法精确采样到某一个给定状态,如下图所示: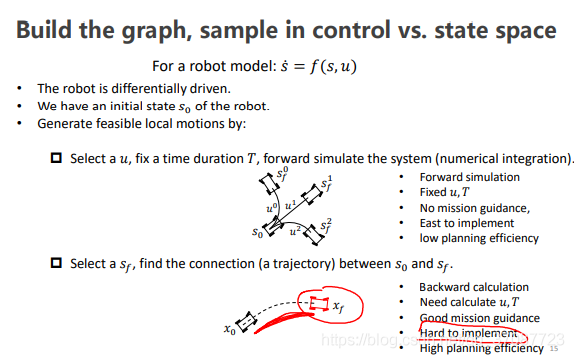
sample in control space(是离散化的一系列控制量产生轨迹,进行延伸,没有目标导向)
选择一个𝑢,固定一个时间段𝑇,正向模拟系统(数值积分)。
正向模拟
确定的u,T
无任务导向(缺点)
容易实施
低效率
sample in state space(是在地图中每个离散点的状态采样反推轨迹,可以有目的的向目标点延伸)
选择状态s_f,寻找从s_0到s_f的轨迹
反向计算:
需要知道T,u(或者估计假设等)
很难实施
具有任务导向性
sample in control space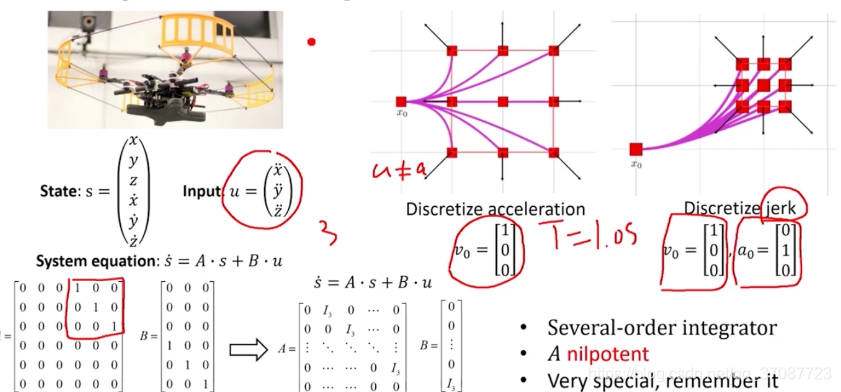
选择加速度作为控制输入,紫色的线代表(feasible motion)T=1s(假设)时间内机器人的状态轨迹,为啥会呈现抛物线形状,这是由于物体匀加速运动导致的;jerk:加速度求导 x求三次导
A nilpotent:幂零矩阵(会在A的某次方为零,方便计算)

e^At:状态转移矩阵
F(t):零输入响应
G(t):零状态响应
Um:给定输入
S(t):状态响应
其实就是匀加速运动在高维状态的叠加
对采样结果进行进一步的离散化,控制空间中的最终采样结果如下图:
The lattice graph obtained by searching
搜索得到的点阵图
需要要有目标性,不需要完整的搜索
在搜索过程中,可以根据需要建立图形。
•创建节点(状态)和边(初始运动)当节点被新发现时。
•节省计算时间/空间。

步骤:
- 搜索树按某种规则找到一个周期T内的状态S
- 选择一个控制的输入
- 固定一个较短的时间,堆等式进行积分
- 加入没有碰撞的动作到搜索树

构建一个点阵图:
• 给定一个原点。
• 对于原点周围的8个邻居节点,找到可行路径。
• 向外扩展到24个邻居。
• 完整点阵
参考:Generating Near Minimal Spanning Control Sets for Constrained Motion Planning in Discrete State Spaces,Mihail Pivtoraiko and Alonzo Kelly
两层Lattice graph
第一层不同,不同的初始状态
comparison
论文:State Space Sampling of Feasible Motions for High-Performance Mobile Robot Navigation in Complex Environments,
Thomas M. Howard, Colin J. Green, and Alonzo Kelly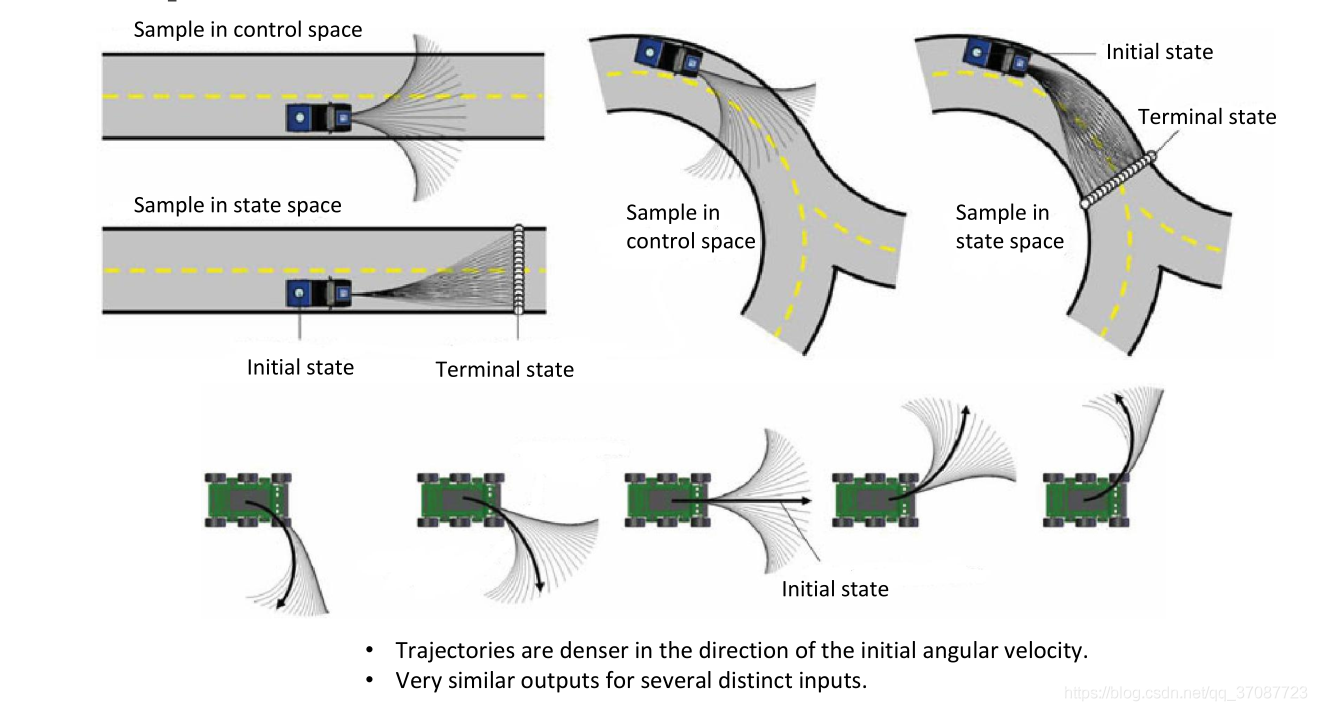
- 在初始角速度方向上轨迹密度更大,受初始化影响很大
- 不同输入的输出非常相似。
- 从图中可以看出,控制空间中的采样没有目的性,离散控制量得到的运动路径是不合格的,会使机器人运动到合理的运动环境之外,得到的局部轨迹仅仅有一部分可以使用;状态空间中的采样可以保证局部轨迹可用。
Boundary Value Problem(BVP)
- BVP是状态采样点阵规划的基础。
- 没有通用的解决方案。只能逐个设计。
- 经常进行复杂的数值优化。
Y:需要求解状态空间采样的问题。
根据边界条件求解方程
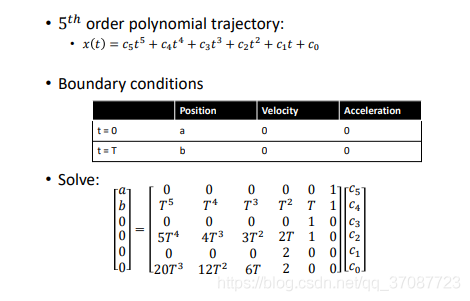
optimal BVP
问题:从一个状态(初始)到另一个状态(结束),如何最小化jerk平方和的积分:
(jerk加加速度)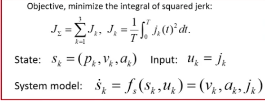
k表示某个轴,
根据庞特里亚的极小值原理,我们首先引入协态:根据system model来定义
定义哈密尔顿函数


首先定义cost function ,然后定义Hamilton中间变量λ \lambdaλ,使用极小值原理选取u使得H函数最小
参考
A Computationally Efficient Motion Primitive for Quadrocopter Trajectory Generation, Mark W. Mueller, Markus Hehn, and Raffaello D’Andrea
Dynamic Programming and Optimal Control, D. P. Bertsekas
example optimal state
先简化为1轴的问题,最小化无人机的jerk
没有边界条件,没有final state,一定到达的硬约束。根据s(T)=s_f来求解
最后转换为多项式求根
如果有一些变量不需要给定,求最优也能行
同时,可以将代价函数J 转变为关于时间T 的函数,对代价函数求极小值可以求得最优的时间T 如下:
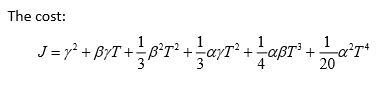
将两点的边界状态代入状态方程,可以求得α , β , γ 的值,OBVP问题求解完成:
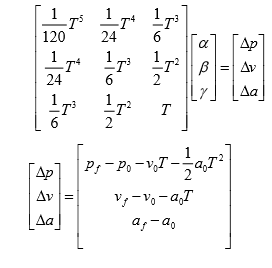
最终求多项式的根T
整个推导过程详解:
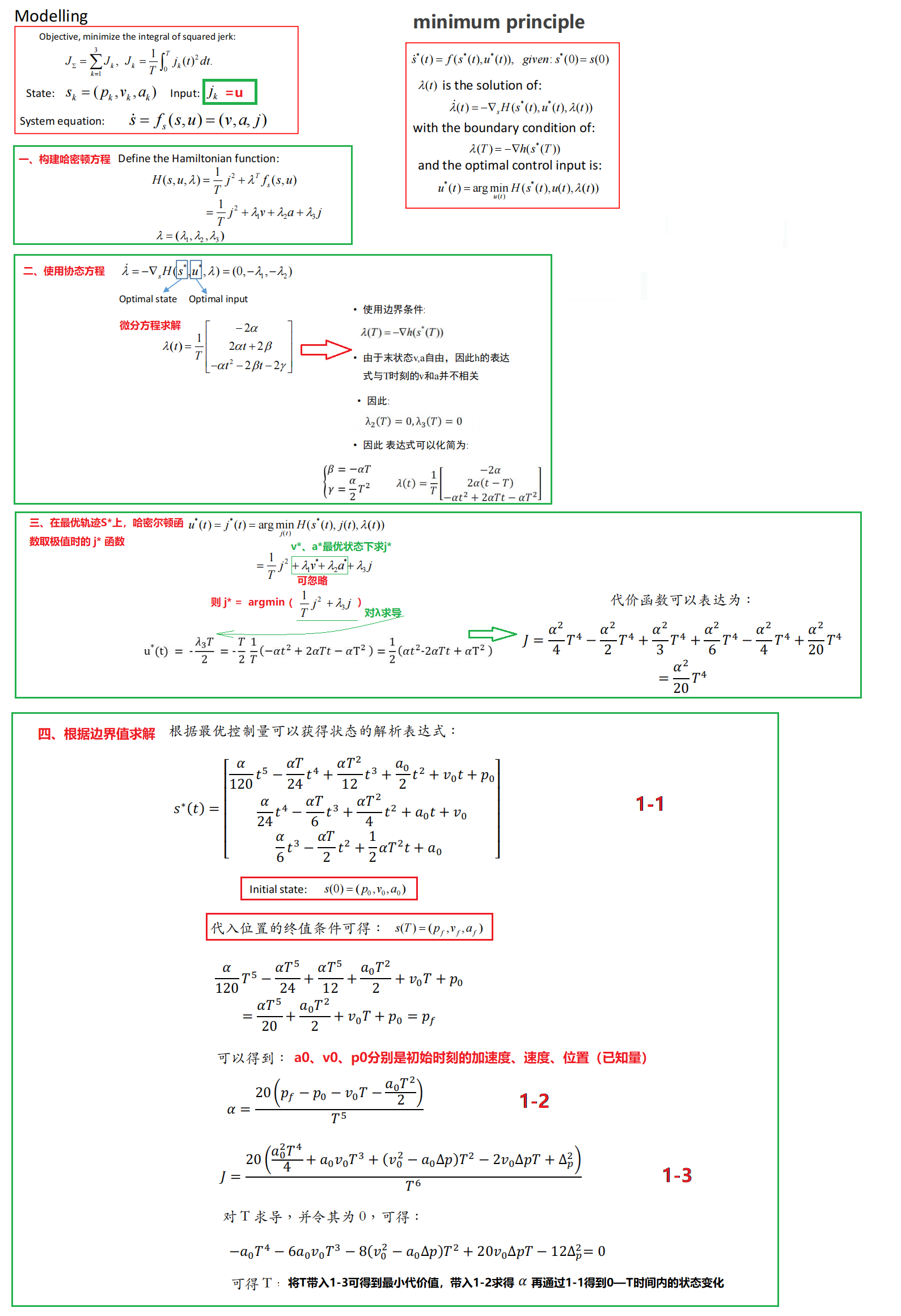
reference
example
Optimal Rough Terrain Trajectory Generation for Wheeled Mobile Robots, Thomas M. Howard Alonzo Kelly
A Computationally Efficient Motion Primitive for Quadrocopter Trajectory。
Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments , Dmitri Dolgov , Sebastian Thrun,
Michael Montemerlo , James Diebel。
https://pythonrobotics.readthedocs.io/en/latest/modules/path_planning.html#optimal-trajectory-in-a-frenet-frame。
参考论文Generation, Mark W. Mueller, Markus Hehn , and Raffaello D’Andrea
Dynamic Programming and Optimal Control, D. P. Bertseka
轨迹库
根据评分函数来确定那个轨迹较合适
Heuristic heuristic
原则:只解决一个简单的问题,
两种做法
•假定不存在障碍
•假设不考虑动力学
Planning in Frenet-serret Frame
参考文献
Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame, Moritz Werling, Julius Ziegler, Sören Kammel, and Sebastian Thrun。
Optimal trajectories for time-critical street scenarios using discretized terminal manifolds , Moritz Werling, Sören Kammel , Julius Ziegler and Lutz Gröll。
作业
OBVP 问题求解


 浙公网安备 33010602011771号
浙公网安备 33010602011771号