自动驾驶运动规划-Reeds Shepp曲线
自动驾驶运动规划-Reeds Shepp曲线
相比于Dubins Car只允许车辆向前运动，Reeds Shepp Car既允许车辆向前运动，也允许车辆向后运动。
Reeds Shepp Car运动规划
1、车辆模型
车辆运动模型仍然采用Simple Car Model，但增加对车辆运动方向的描述，运动方程如下：
其中，，
。当
时，表示车辆向前运动；
时，表示车辆向后运动。
2、Reeds-Shepp Car
J Reeds和L Shepp证明Reeds Shepp Car从起点到终点
的最短路径一定是下面的word的其中之一。word中的"|"表示车辆运动朝向由正向转为反向或者由反向转为正向。
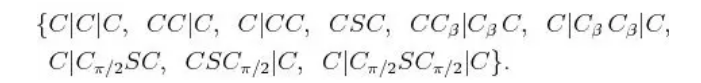图片来源：Planning Algorithm，http://planning.cs.uiuc.edu/node822.html
每个word都由，
，
，
，
，
这六种primitives组成，其中
表示车辆左转前进；
表示车辆左转后退；
表示车辆右转前进；
表示车辆右转后退；
表示车辆直行前进；
表示车辆直行后退。
Reeds and Shepp曲线的word所有组合不超过48种，所有的组合一一枚举如下：
图片来源：Planning Algorithm，http://planning.cs.uiuc.edu/node822.html
3、计算优化
3.1 位置姿态统一化
车辆的起点和终点的位置姿态是难以穷举的，所以一般在计算之前，会将车辆的姿态归一化：
起始姿态：；
目标姿态：；其中，
车辆的转弯半径： r = 1;
假设车辆的初始姿态为，目标姿态
，车辆的转向半径为r =
，如何实现姿态的归一化呢，实际上归一化的过程就是向量的平移和旋转过程。归一化：为了方便起见Reeds-Shepp中最小转向半径强制设置为1，如果车辆的实际最小转向半径不是1，可也通过适当放缩终点坐标来计算该曲线。比如如果一个车辆的最小转向半径为10，终点坐标为x,y，如果我们在计算曲线的时候将终点设为x/10,y/10，计算所得路径放大10倍曲线的转向半径就是10，终点也是x,y，所得曲线就是我们所期望曲线。
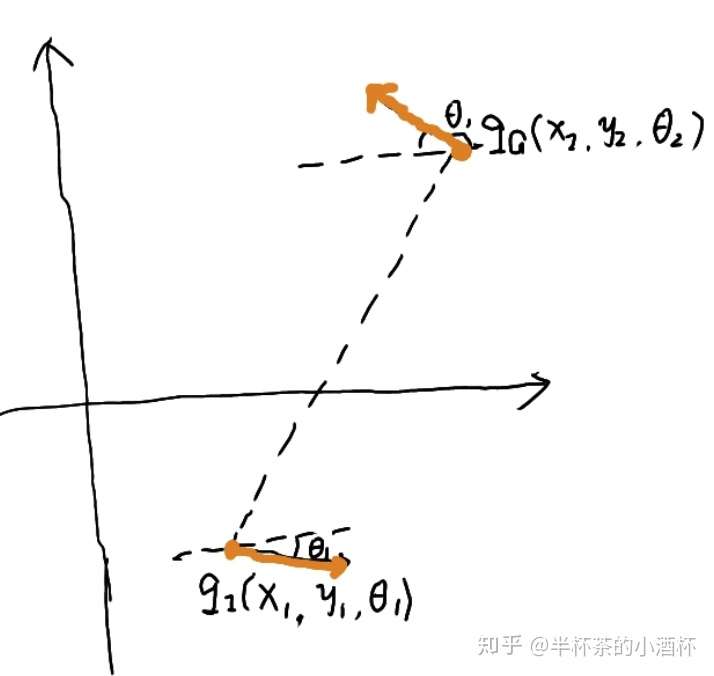
首先将向量平移到坐标原点(0,0)。平移
到O(0, 0)，平移向量为
；对
应用同样的平移向量:
，最后得到平移后的向量：
应用旋转矩阵，将车辆的起点朝向转到x轴正向：
旋转之后，目标位置朝向更新为。
将车辆转向半径缩放到1，于是最终得到车辆运动的起始姿态：
目标姿态：
代码如下:
double x1 = s1->getX(), y1 = s1->getY(), th1 = s1->getYaw();
double x2 = s2->getX(), y2 = s2->getY(), th2 = s2->getYaw();
double dx = x2 - x1, dy = y2 - y1, c = cos(th1), s = sin(th1);
double x = c * dx + s * dy, y = -s * dx + c * dy, phi = th2 - th1;
return ::reedsShepp(x / rho_, y / rho_, phi)
3.2 利用对称关系降低求解复杂度
Reeds Shepp曲线有48种组合，编程时一一编码计算比较麻烦，因此可以利用其对称性降低求解工作量。
以转向不同的CSC类型为例，它包含4种曲线类型：、
、
、
，我们只需要编码推导得到
的计算过程，其它几种直接可以通过对称性关系得到车辆运动路径。
给定车辆起始姿态，目标姿态
，可以得到
的运动路径如下：
{ Steering: left Gear: forward distance: 0.63 }
{ Steering: straight Gear: forward distance: 4.02 }
{ Steering: right Gear: forward distance: 0.11 }
对应的效果如下：
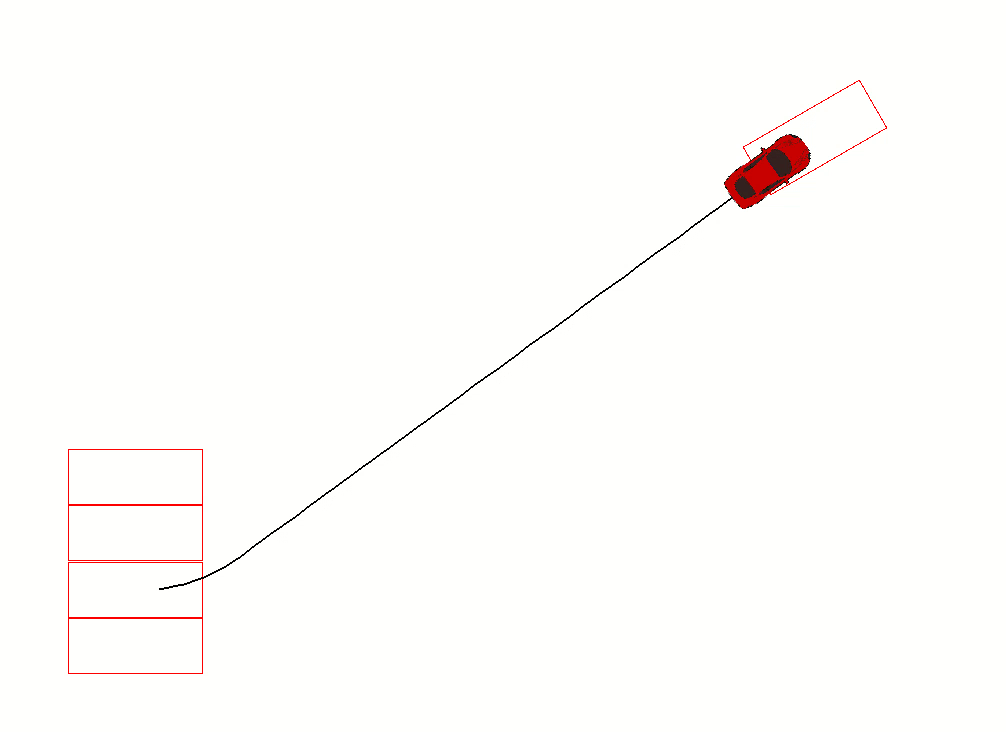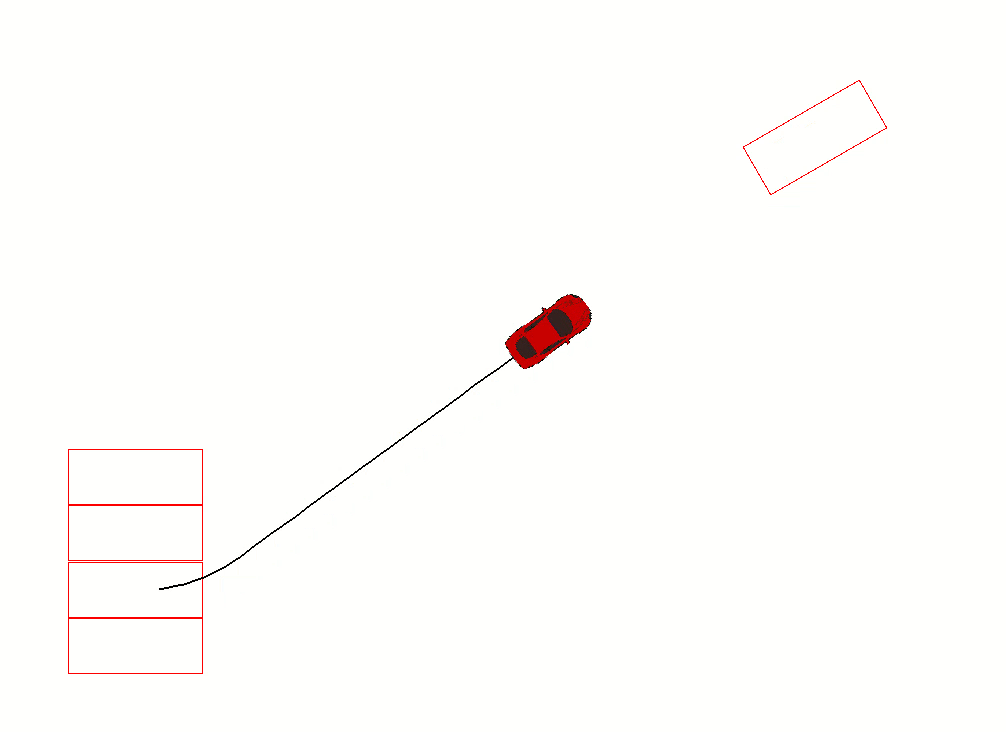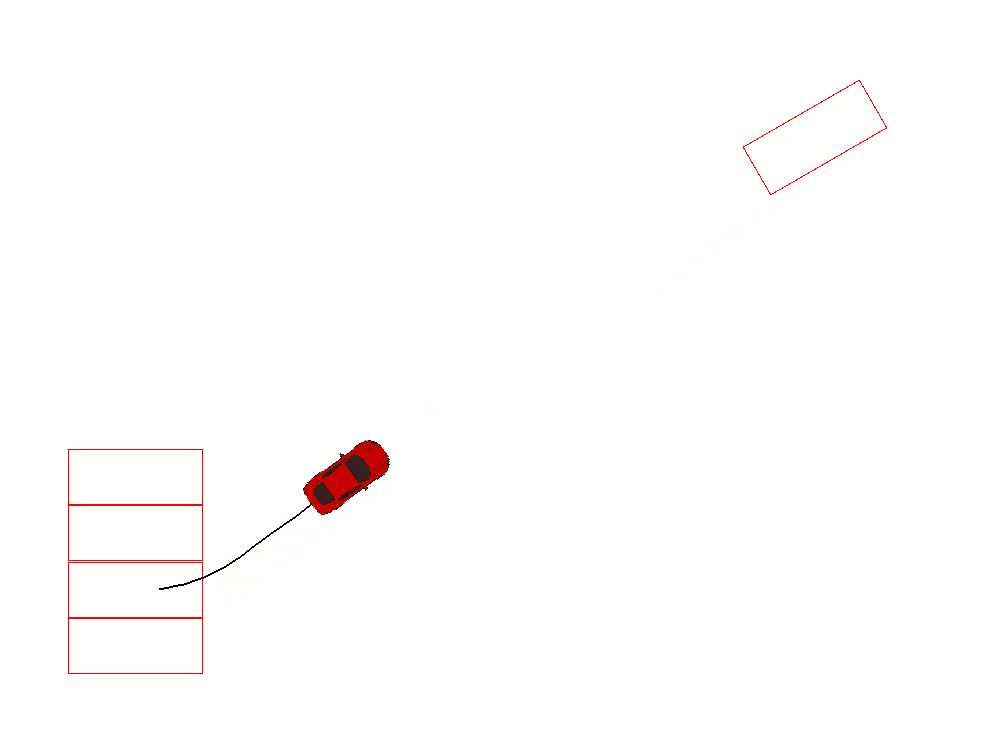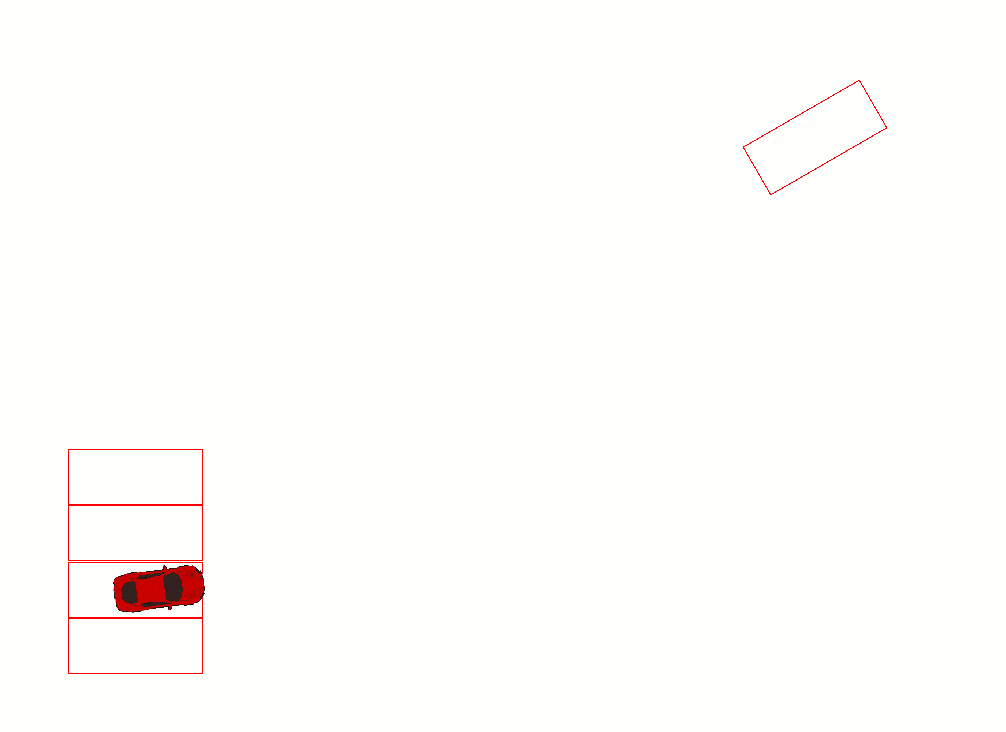
L^{+}S^{+}R^{+}
下面看看利用对称性求解其它几种路径的方法。
3.2.1 timefilp对称性
假设我们推导出从起始姿态达到目标姿态
的路径计算方法：
path = calc_path(,
,
,
,
,
)
利用对称性，将目标Pose修改为，代入同样的Path计算函数：
path = calc_path(,
,
, -
,
, -
)
就得到从到
的
类型的运动路径。
计算出的的车辆运动路径如下：
{ Steering: left Gear: backward distance: -2.85 }
{ Steering: straight Gear: backward distance: 4.02 }
{ Steering: right Gear: backward distance: -2.32 }
下面是车辆的运动效果，一路倒车进入另一个车位。
3.2.2 reflect对称性
将目标姿态修改为，代入同样的Path计算函数：
path = calc_path(,
,
,
, -
, -
)
就得到从到
的
类型的运动路径。
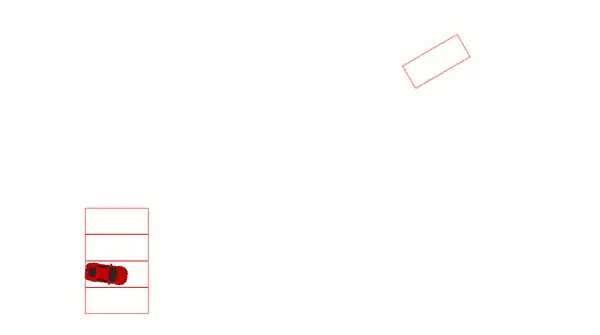
计算出的的车辆运动路径如下：
{ Steering: right Gear: forward distance: -0.56 }
{ Steering: straight Gear: forward distance: 5.28 }
{ Steering: left Gear: forward distance: -0.03 }
下面是车辆先右转、再直行、再左转从一个车位进入另一个车位的运动效果。
R^{+}S^{+}L^{+}类型曲线
3.2.3 timeflip + reflect
结合timeflip对称性和reflect对称性，将目标姿态修改为，代入同样的Path计算函数：
path = calc_path(,
,
, -
, -
,
)
就得到从到
的
类型的运动路径。
计算出的的车辆运动路径如下：
{ Steering: right Gear: backward distance: -1.86 }
{ Steering: straight Gear: backward distance: 5.28 }
{ Steering: left Gear: backward distance: -2.38 }
下面是车辆先右转、再直行、再左转，全程倒车从一个车位进入另一个车位的运动效果。
R^{-}S^{-}L^{-}类型曲线
通过对称性，48种不同的Reeds Shepp曲线通过不超过12个函数就可以得到全部运动路径。
参考链接
1、Optimal paths for a car that goes both forwards and backwards, J Reeds, L Shepp - Pacific journal of mathematics, 1990
2、OMPL的Reeds Sheep实现代码。(https://ompl.kavrakilab.org/ReedsSheppStateSpace_8cpp_source.html)
3、Reeds Sheep的Python代码实现。(https://github.com/nathanlct/reeds-shepp-curves/blob/master/reeds_shepp.py)
转自：https://zhuanlan.zhihu.com/p/122544884
